leetcode-回溯③

题77

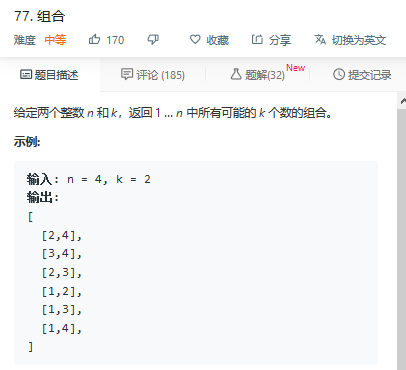
回溯：

class Solution:
    def combine(self, n: int, k: int) -> List[List[int]]:
        res = []
        def backtrack(i,temp_list):
            if len(temp_list)==k:
                res.append(temp_list)
            for j in range(i,n+1):
                backtrack(j+1,temp_list+[j])
        backtrack(1,[])
        return res

题78：

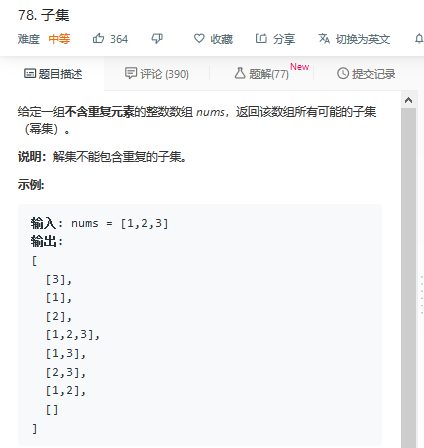
回溯：

class Solution:
    def subsets(self, nums: List[int]) -> List[List[int]]:
        res = []
        def helper(i,tmp):
            res.append(tmp)
            for j in range(i,len(nums)):
                helper(j+1,tmp+[nums[j]])
        helper(0,[])
        return res

题90：

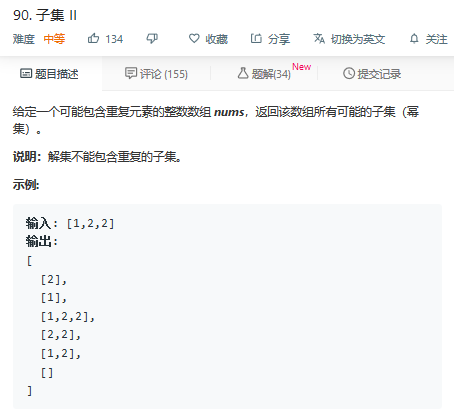
回溯：

class Solution:
    def subsetsWithDup(self, nums: List[int]) -> List[List[int]]:
        res = []
        n = len(nums)
        nums.sort()
        def helper(idx, tmp):
            res.append(tmp)
            for i in range(idx, n):
                if i > idx and nums[i] == nums[i-1]:
                    continue
                helper(i+1, tmp + [nums[i]])
        helper(0, [])
        return res

题93

回溯：

class Solution:
    def restoreIpAddresses(self, s: str) -> List[str]:
        res = []
        n = len(s)

        def backtrack(i, tmp, flag):
            if i == n and flag == 0:
                res.append(tmp[:-1])
                return
            if flag < 0:
                return
            for j in range(i, i + 3):
                if j < n:
                    if i == j and s[j] == "":
                        backtrack(j + 1, tmp + s[j] + ".", flag - 1)
                        break
                    if 0 < int(s[i:j + 1]) <= 255:
                        backtrack(j + 1, tmp + s[i:j + 1] + ".", flag - 1)

        backtrack(0, "", 4)
        return res

题131

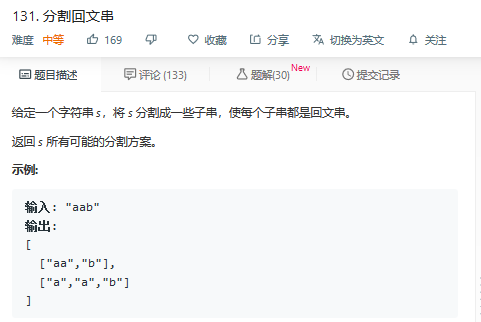
回溯;

class Solution:
    def partition(self, s: str) -> List[List[str]]:
        res = []
        temp = []
        def backtrack(s,temp):
            if not s:
                res.append(temp)
            for i in range(1,len(s)+1):
                if s[:i][::-1] == s[:i]:
                    backtrack(s[i:],temp+[s[:i]])
        backtrack(s,[])
        return res

题216：

回溯：

class Solution:
    def combinationSum3(self, k: int, n: int) -> List[List[int]]:
        res = []
        def helper(k,n,start,tmp):
            if k==0:
                if n==0:
                    res.append(tmp)
                return
            for i in range(start,10):
                if n - i < 0:break
                helper(k-1,n-i,i+1,tmp+[i])
        helper(k,n,1,[])
        return res