剑指offer-青蛙变态跳台阶-全概率公式






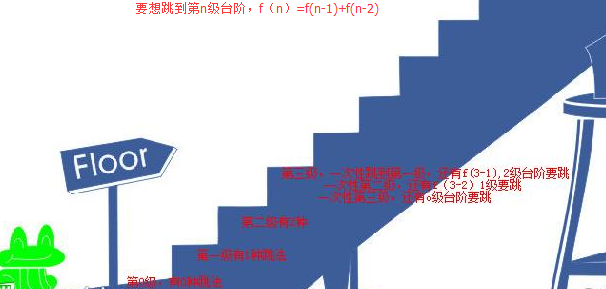
剑指offer-青蛙变态跳台阶-全概率公式的更多相关文章
- [剑指Offer]2.变态跳台阶
题目 一仅仅青蛙一次能够跳上1级台阶,也能够跳上2级--它也能够跳上n级. 求该青蛙跳上一个n级的台阶总共同拥有多少种跳法. 思路 用Fib(n)表示青蛙跳上n阶台阶的跳法数,设定Fib(0) = 1 ...
- Go语言实现:【剑指offer】变态跳台阶
该题目来源于牛客网<剑指offer>专题. 一只青蛙一次可以跳上1级台阶,也可以跳上2级--它也可以跳上n级.求该青蛙跳上一个n级的台阶总共有多少种跳法. 找规律: 1阶:1种: 2阶:2 ...
- 剑指OFFER之变态跳台阶(九度OJ1389)
题目描述: 一只青蛙一次可以跳上1级台阶,也可以跳上2级……它也可以跳上n级.求该青蛙跳上一个n级的台阶总共有多少种跳法. 输入: 输入可能包含多个测试样例,对于每个测试案例, 输入包括一个整数n(1 ...
- 剑指offer:变态跳台阶
题目描述 一只青蛙一次可以跳上1级台阶,也可以跳上2级……它也可以跳上n级.求该青蛙跳上一个n级的台阶总共有多少种跳法. 思路 首先想到的解决方案是根据普通跳台阶题目改编,因为可以跳任意级,所以要 ...
- 剑指Offer 9. 变态跳台阶 (递归)
题目描述 一只青蛙一次可以跳上1级台阶,也可以跳上2级……它也可以跳上n级.求该青蛙跳上一个n级的台阶总共有多少种跳法. 题目地址 https://www.nowcoder.com/practice/ ...
- 【剑指offer】变态跳台阶
一.题目: 一只青蛙一次可以跳上1级台阶,也可以跳上2级……它也可以跳上n级.求该青蛙跳上一个n级的台阶总共有多少种跳法. 二.思路: f(n)=f(n-1)+f(n-2)+...+f(0),f(1) ...
- 剑指offer 09变态跳台阶
一只青蛙一次可以跳上1级台阶,也可以跳上2级……它也可以跳上n级.求该青蛙跳上一个n级的台阶总共有多少种跳法. java版本: public class Solution { public stati ...
- [剑指Offer] 9.变态跳台阶
题目描述 一只青蛙一次可以跳上1级台阶,也可以跳上2级……它也可以跳上n级.求该青蛙跳上一个n级的台阶总共有多少种跳法. [思路1]每个台阶都有跳与不跳两种可能性(最后一个台阶除外),最后一个台阶必 ...
- 《剑指offer》变态跳台阶
一.题目描述 一只青蛙一次可以跳上1级台阶,也可以跳上2级--它也可以跳上n级.求该青蛙跳上一个n级的台阶总共有多少种跳法. 二.输入描述 n级台阶 三.输出描述 一共有多少种不同的跳法 四.牛客网提 ...
- 【牛客网-剑指offer】变态跳台阶
题目: 一只青蛙一次可以跳上1级台阶,也可以跳上2级--它也可以跳上n级.求该青蛙跳上一个n级的台阶总共有多少种跳法. 考点: 递归和循环 分析: 台阶数 跳法 1 1 2 2 3 4 4 8 5 1 ...
随机推荐
- 20170612xlVBA多文件多类别分类求和匹配
Public Sub Basic_CodeFrame() AppSettings 'On Error GoTo ErrHandler Dim StartTime, UsedTime As Varian ...
- poj2686 状压dp入门
状压dp第一题:很多东西没看懂,慢慢来,状压dp主要运用了位运算,二进制处理 集合{0,1,2,3,....,n-1}的子集可以用下面的方法编码成整数 像这样,一些集合运算就可以用如下的方法来操作: ...
- IDEA编译时出现"cannot resolve symbol"的问题时的解决方法。
IDEA编译时出现cannot resolve symbol的报错时,(老表的问题出现在另一台电脑上,所以现在没办法给大家截图报错时的图,今天是周末没用那台电脑,突然想起来就想把它写下来,抱歉抱歉!! ...
- python-day48--mysql之视图、触发器、事务、存储过程、函数
一.视图(不推荐使用) 1).视图是一个虚拟表(非真实存在) 2).使用视图我们可以把查询过程中的临时表摘出来,用视图去实现,这样以后再想操作该临时表的数据时就无需重写复杂的sql了,直接去视图中查找 ...
- nyoj-310-河南省第四届省赛题目-二分+dinic
SECRET 时间限制:3000 ms | 内存限制:65535 KB 难度:6 描述 Dr.Kong is constructing a new machine and wishes to ...
- UVA-1663 Purifying Machine (最大匹配数)
题目大意:每一个01串中最多含有一个‘*’,‘*’既可表示0也可表示1,给出一些等长的这样的01串,问最少能用多少个这样的串表示出这些串.如:000.010.0*1表示000.010.001.011, ...
- RAC配置(启停库)
关库顺序 :先关闭数据库 然后关闭节点资源 [root@rac1 ~]# srvctl stop database -d 数据库名[root@rac1 ~]# srvctl stop ins ...
- logback 范例
<?xml version="1.0" encoding="UTF-8"?> <configuration debug="false ...
- spring cloud学习(六)Spring Cloud Config
Spring Cloud Config 参考个人项目 参考个人项目 : (希望大家能给个star~) https://github.com/FunriLy/springcloud-study/tree ...
- spring cloud 学习(二)关于 Eureka 的学习笔记
关于 Eureka 的学习笔记 个人博客地址 : https://zggdczfr.cn/ ,欢迎光临~ 前言 Eureka是Netflix开发的服务发现组件,本身是一个基于REST的服务.Sprin ...
