Let Me Count The Ways(Kickstart Round H 2018)

题目链接：https://code.google.com/codejam/contest/3324486/dashboard#s=p2

题目：

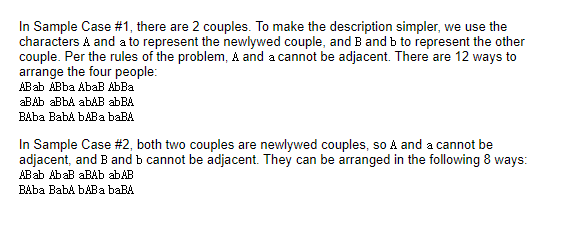
思路：

　　

代码实现如下：

 #include <set>
 #include <map>
 #include <deque>
 #include <queue>
 #include <stack>
 #include <cmath>
 #include <ctime>
 #include <bitset>
 #include <cstdio>
 #include <string>
 #include <vector>
 #include <cstdlib>
 #include <cstring>
 #include <iostream>
 #include <algorithm>
 using namespace std;

 typedef long long LL;
 typedef pair<LL, LL> pLL;
 typedef pair<LL, int> pli;
 typedef pair<int, LL> pil;;
 typedef pair<int, int> pii;
 typedef unsigned long long uLL;

 #define lson rt<<1
 #define rson rt<<1|1
 #define lowbit(x) x&(-x)
 #define  name2str(name) (#name)
 #define bug printf("*********\n")
 #define debug(x) cout<<#x"=["<<x<<"]" <<endl
 #define FIN freopen("D://code//in.txt", "r", stdin)
 #define IO ios::sync_with_stdio(false),cin.tie(0)

 const double eps = 1e-;
 const int mod = ;
 const int maxn = 2e5 + ;
 const double pi = acos(-);
 const int inf = 0x3f3f3f3f;
 const LL INF = 0x3f3f3f3f3f3f3f3fLL;

 int t, n, m;
 LL A[maxn], inv[maxn];

 LL Mod_Pow(LL x, int n) {
     LL res = ;
     while(n) {
         if(n & ) res = res * x % mod;
         x = x * x % mod;
         n >>= ;
     }
     return res;
 }

 void init() {
     A[] = ;
     for(int i = ; i < maxn; i++) A[i] = (A[i-] * i) % mod;
     inv[maxn-] = Mod_Pow(A[maxn-], mod - );
     for(int i = maxn - ; i >= ; i--) {
         inv[i] = inv[i+] * (i + ) % mod;
     }
 }

 int Com(int n, int m) {
     if(n <  || m <  || m > n) return ;
     if(m ==  || m == n) return ;
     return ((A[n] * inv[n-m] % mod) * inv[m]) % mod;
 }

 int main() {
 #ifndef ONLINE_JUDGE
     FIN;
 #endif
     init();
     int icase = ;
     scanf("%d", &t);
     while(t--) {
         scanf("%d%d", &n, &m);
         LL sum = ;
         for(int i = ; i <= m; i++) {
             if(i %  == ) {
                 sum = (sum + ((Com(m, i) * Mod_Pow(, i) % mod) * A[ * n - i]) % mod) % mod;
             } else {
                 sum = (sum - ((Com(m, i) * Mod_Pow(, i) % mod) * A[ * n - i]) % mod + mod) % mod;
             }
         }
         printf("Case #%d: %lld\n", ++icase, sum % mod);
     }
     return ;
 }