反卷积Deconvolution

反卷积（转置卷积、空洞卷积（微步卷积））近几年用得较多，本篇博客主要是介绍一下反卷积，尤其是怎么计算反卷积（选择反卷积的相关参数）

图1 空洞卷积（微步卷积）的例子，其中下面的图是输入，上面的图是输出，显然这是一个upsampling的过程，我们也称为反卷积。

首先，既然本文题名为反卷积（Deconvolution），当然就是要介绍各种反卷积，不得不说的是随着近几年人工智能如火如荼，大牛纷纷在各个角度开始深入研究这个深度学习，这当然就是更广了同时也更深了，但是只要抓住深度学习的命门，其实很多工作都是顺理成章的，没有想象中的那么复杂，也许这也是我对深度学习的一点小小的感悟。反卷积，它有这几个比较熟悉的名字，例如转置卷积、上采样、空洞卷积、微步卷积，但我们认为，最直接的就是反卷积=上采样=（转置卷积+微步卷积）⊆ 空洞卷积=一般意义上的广义卷积（包含上采样和下采样）。

另外，在概念上，我们只是将其称为反卷积，这不是通过数学意义上的严格证明，其实只是说恢复了特征图的尺寸大小，数值上存在差异。

为了方便说明，对二维的离散卷积，定义如下：

• 方形的特征输入（i1=i2=i）
• 方形的卷积核尺寸（k1=k2=k）
• 每个维度相同的步长（s1=s2=s）
• 每个维度相同的padding (p1=p2=p)

下图表示参数为 (i=5,k=3,s=2,p=1) 的卷积计算过程，从计算结果可以看出输出特征的尺寸为 (o1=o2=o=3)。

图2  卷积图示例1

下图表示参数为 (i=6,k=3,s=2,p=1)的卷积计算过程，从计算结果可以看出输出特征的尺寸为 (o1=o2=o=3)。

图3  卷积图示例2

从上述两个例子我们可以总结出卷积层输入特征与输出特征尺寸和卷积核相关参数的关系为：

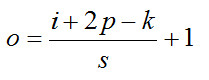
反卷积层

同理，定义反卷积的参数为上述卷积参数后加 ′ 表示。

图4  转置卷积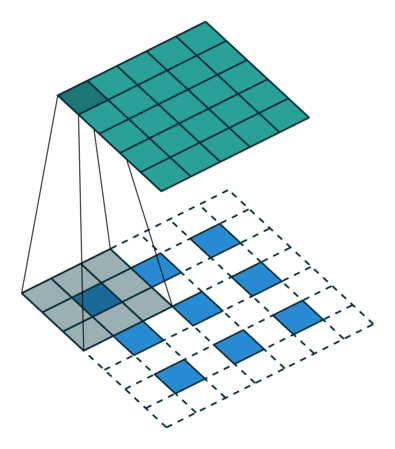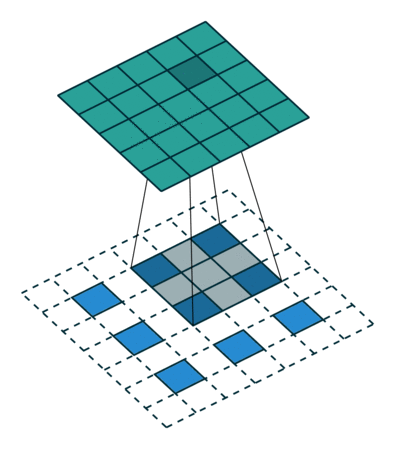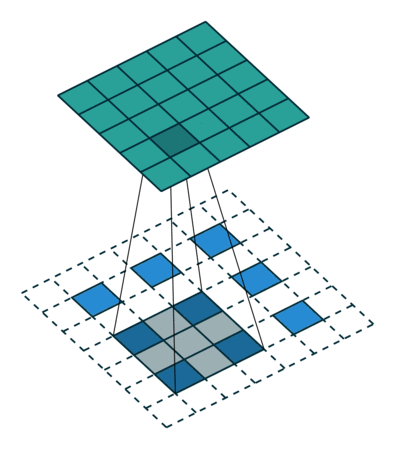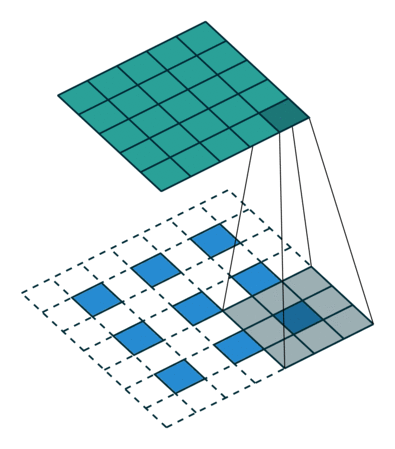

图5  微步卷积

可推得计算公式为：o′=s(i−1)+k−2p。比如10*10变成19*19，可知k=3，p=1，s=2。

另外，微步卷积新的卷积核K=dilation*(k-1)+1，显然dilation=1就相当于一般意义上的卷积，所以说空洞卷积更具一般性，事实也证明如此，Caffe中就是实现了空洞卷积和转置卷积。

进一步阅读请参考：

1. 如何理解空洞卷积

2.如何理解反卷积

3.反卷积