Poisson Distribution——泊松分布

　　老师留个小作业，用EXCEL做不同lambda（np）的泊松分布图，这里分别用EXCEL，Python，MATLAB和R简单画一下。

　　1. EXCEL

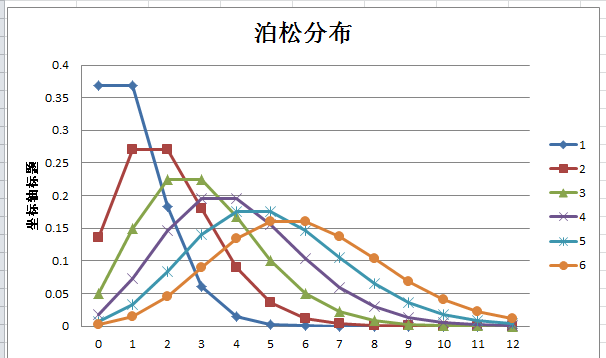
　　运用EXCEL统计学公式，POISSON，算出各个数据，作图。资料参考这里。

　　=POISSON.DIST(B$1,$A2,0)

　　注意这里绝对引用的方式，写完公式之后，直接上下左右拖动鼠标即可自动填充。之后插入图表。如下。

　　

　　2.Python

　　这里stats.poisson.pmf中的pmf是probability mass function（概率质量函数）的缩写。

　　以下引自WIKI：

　　在概率论中，概率质量函数（probability mass function，简写为pmf）是离散随机变量在各特定取值上的概率。

　　概率质量函数和概率密度函数不同之处在于：概率质量函数是对离散随机变量定义的，本身代表该值的概率；

　　概率密度函数是对连续随机变量定义的，本身不是概率，只有对连续随机变量的概率密度函数在某区间内进行积分后才是概率。

import scipy.stats as stats
import matplotlib.pyplot as plt

k = range(0,13)
for ld in range(7):
    y = stats.poisson.pmf(k,ld)
    plt.xlabel('K')
    plt.ylabel('P')
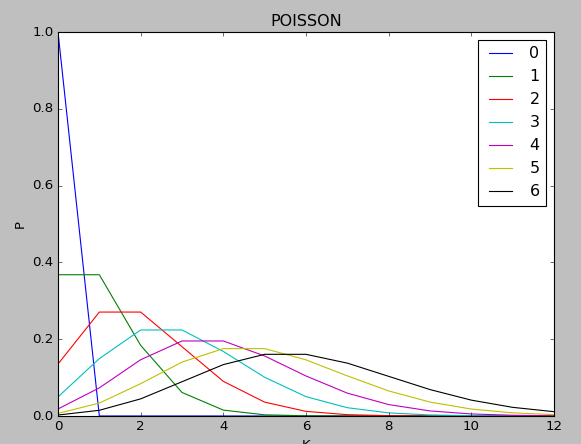
    plt.title('POISSON')
    plt.plot(y,label=str(ld))

plt.legend()
plt.show()

　　输出图形：

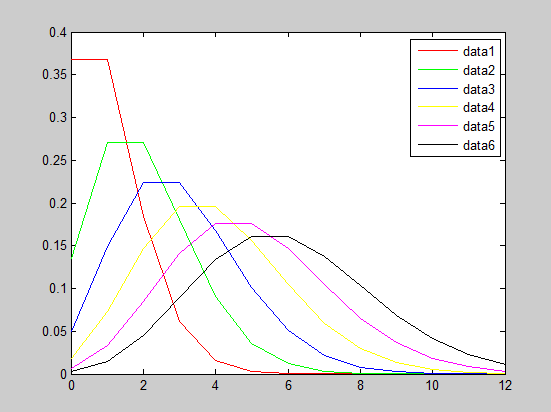
　　3.MATLAB

x=0:12;
c = ['r','g','b','y','m','k'];
for i = (1:6)
    y=poisspdf(x,i);
    plot(x,y,c(i));
    hold on
end

　　输出如下：

　　

　　4.R

pmf <- function(lambda){
  y = list()
  for(k in 0:12){
      y[k+1] <- round(dpois(x=k,lambda),3)
  }
  return(y)
}

mycols <- runif(10,min=1,max=length(colors()))

for(i in 1:6){
  par(new=TRUE)
  y = plot(c(0:12),pmf(i),type='l',ylim=c(0,0.4),col = mycols[i])
  }

　　输出：

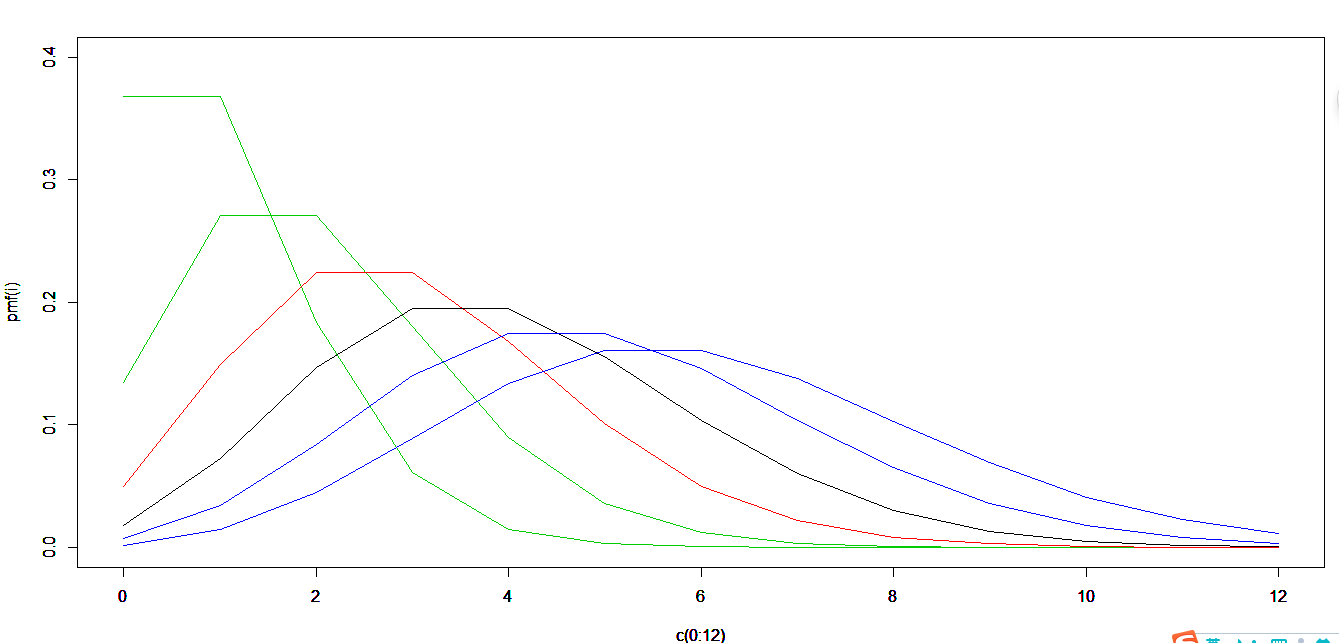
　　美中不足的是，楼主不知道如何为每条线设置标签。查了一下午legend函数，还是没搞定。。。

　　解决了回头补充吧。。。

　　###################################################

　　来补充了。。。问了问大佬们，给出下面的方法

pmf <- function(lambda){
  y = list()
  for(k in 0:12){
    y[k+1] <- round(dpois(x=k,lambda),3)
  }
  y = unlist(y)
  return(y)
}

mycols <- runif(10,min=1,max=length(colors()))

y_data <- matrix(unlist(lapply(1:6,FUN = pmf)),ncol = 6)

matplot(y_data,type='l',ylim=c(0,0.4),col = mycols)

colnames(y_data) = 1:ncol(y_data)
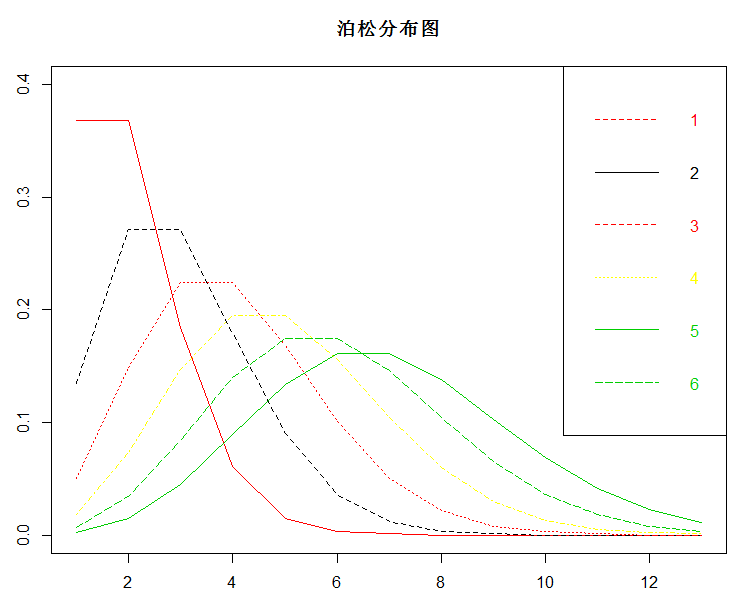
matplot(y_data,type='l',sub = "标记",ylim=c(0,0.4),col = mycols,main = "泊松分布图")

legend(
  "topright"
  ,legend = colnames(y_data)
  ,text.col = mycols
  ,col = mycols
  ,lty = mycols
)

　　输出：