梯度下降、随机梯度下降、方差减小的梯度下降(matlab实现)

梯度下降代码：

function [ theta, J_history ] = GradinentDecent( X, y, theta, alpha, num_iter )

m = length(y);

J_history = zeros(20, 1);

i = 0;

temp = 0;

for iter = 1:num_iter
     temp = temp +1;
     theta = theta - alpha / m * X' * (X*theta - y);
     if temp>=100
         temp = 0;
         i = i + 1;
         J_history(i) = ComputeCost(X, y, theta);
     end

end

end

随机梯度下降代码：

function [ theta,J_history ] = StochasticGD( X, y, theta, alpha, num_iter )

m = length(y);

J_history = zeros(20, 1);

temp = 0;

n = 0;

for iter = 1:num_iter
     temp = temp + 1;
     index = randi(m);
     theta = theta -alpha *  (X(index, :) * theta - y(index)) * X(index, :)';
     if temp>=100
         temp = 0;
         n = n + 1;
         J_history(n) = ComputeCost(X, y, theta);
     end

end

end

方差减小的梯度下降(SVRG)：

function [ theta_old, J_history ] = SVRG( X, y, theta, alpha )

theta_old = theta;

n = length(y);

J_history = zeros(20,1);

m = 2 * n;

for i = 1:20
     theta_ = theta_old;
     Mu = 1/n *  X' * (X*theta_ - y);
     theta_0 = theta_;
     for j = 1:m
         index = randi(n);
         GD_one = (X(index, :) * theta_0 - y(index)) * X(index, :)';
         GD_ = (X(index, :) * theta_ - y(index)) * X(index, :)';
         theta_t = theta_0 - alpha * (GD_one - GD_ + Mu);
         theta_0 = theta_t;
     end
     J_history(i) = ComputeCost(X, y, theta_t);
     theta_old = theta_t;

end

end

损失函数：

function J = ComputeCost( X, y, theta )

m = length(y);

J = sum((X*theta - y).^2) / (2*m);

end

主程序代码：

%% clean workspace

clc;

clear;

close all;

%% plot data

fprintf('plot data... \n');

X = load('ex2x.dat');

y = load('ex2y.dat');

m = length(y);

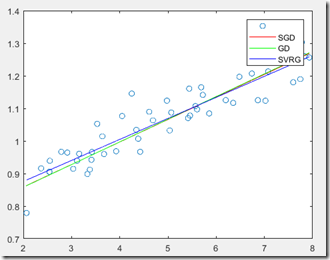
figure;

plot(X,y,'o');

%% gradient decent

fprintf('Runing gradient decent... \n');

X = [ones(m,1),X];

theta_SGD = zeros(2, 1);

theta_GD = zeros(2, 1);

theta_SVRG = zeros(2, 1);

Iteration = 2000;

alpha = 0.015;

alpha1 = 0.025;

[theta ,J]= StochasticGD(X, y, theta_SGD, alpha, Iteration);

[theta1 ,J1]= GradinentDecent(X, y, theta_GD, alpha, Iteration);

[theta2 ,J2]= SVRG(X, y, theta_SVRG, alpha1);

fprintf('SGD: %f %f\n',theta(1),theta(2));

fprintf('GD: %f %f\n',theta1(1),theta1(2));

fprintf('SVRG: %f %f\n',theta2(1),theta2(2));

hold on;

plot(X(:, 2), X*theta, 'r-');

plot(X(:, 2), X*theta1, 'g-');

plot(X(:, 2), X*theta2, 'b-');

legend('','SGD','GD','SVRG');

x_j = 1:1:20;

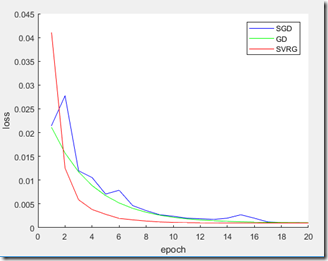
figure;

hold on;

plot(x_j, J, 'b-');

plot(x_j, J1, 'g-');

plot(x_j, J2, 'r-');

legend('SGD','GD','SVRG');

xlabel('epoch')

ylabel('loss')

实验结果：