【CImg】三角形绘制算法实现

这周的CV基础练习是简单的图形绘制：比如说矩形、三角形和圆心什么的。会发现其实矩形和圆形的实现思路都很直白，矩形只需要确认两个对角坐标就可以了，圆心只需要确认圆心和半径，接着就是简单的遍历各个像素点判断。但是，三角形的绘制把数学渣的我难住了，然后去查了一下资料，受到了知乎某位大神的启发：

如下截图：

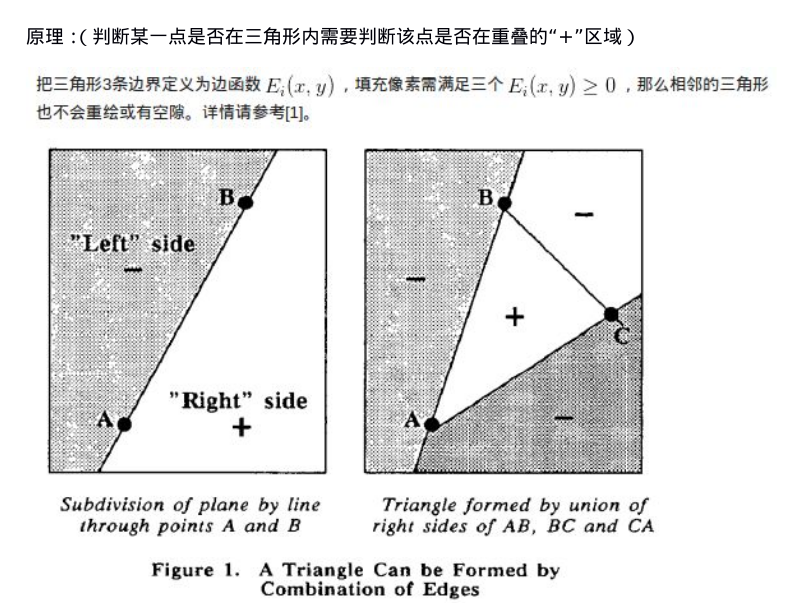
于是有了以下思路：

　　一.实心三角形绘制

　　　　①算出三条直线L1、L2、L3的直线方程，即K1、K2、K3（斜率）和B1、B2、B3（截距）的值

　　　　②设三个顶点为P1、P2、P3，某一个任意位置的像素点P，P1P2的直线为L1.

　　　　③要判断P点是否在L1的“+”一边，则把P、P3分别带入直线方程，算出Y-（KX+B）的值，同时大于0或者同时小于0，则P落在“+”，否则在“-”

　　　　④判断P点是否在三角形内，则需要判断P是否同时落在三条直线的“+”区域，所以要做三次判断

　　二. 三角形边框绘制

　　　　①求出三条直线方程

　　　　②求出三角形范围内的X轴最大最小值，Y轴最大最小值

　　　　③在minX~maxX, minY~maxY的范围内遍历，只要P点落在直线方程上，则可以判断为真，赋上指定的绘制颜色

　　code实现：

 //一个三角形，需要依靠三个顶点来确立，同样还需要颜色以及空心与否等条件
 void drawTri(CImg<unsigned char>& inputImage,  vector<int>& position, vector<int>& color, bool solid ) {
     unsigned int width = inputImage.width();
     unsigned int height = inputImage.height();
     unsigned int depth = inputImage.depth();
     unsigned int spectrum = inputImage.spectrum();

     ////算法优化，尽量地减少遍历范围
     int minX = (position[] > position[] ? position[] : position[]) > position[] ? position[] : (position[] > position[] ? position[] : position[]);
     int maxX = (position[] > position[] ? position[] : position[]) < position[] ? position[] : (position[] > position[] ? position[] : position[]);
     int minY = (position[] > position[] ? position[] : position[]) > position[] ? position[] : (position[] > position[] ? position[] : position[]);
     int maxY = (position[] > position[] ? position[] : position[]) < position[] ? position[] : (position[] > position[] ? position[] : position[]);

     //三条直线方程
     double k1, b1, k2, b2, k3, b3;
     k1 = (position[] - position[]) / (position[] - position[] + 0.0);
     b1 = position[] - k1 * position[];
     k2 = (position[] - position[]) / (position[] - position[] + 0.0);
     b2 = position[] - k2 * position[];
     k3 = (position[] - position[]) / (position[] - position[] + 0.0);
     b3 = position[] - k3 * position[];

     //遍历范围增大，防止边界无法检测 +2, 此处不需要担心超出边界，因为在最后赋值的时候会再判断一次
     for (int x = minX - ; x <= maxX + ; x ++) {
         for (int y = minY - ; y <= maxY + ; y ++) {
             if (y >=  && y < height && x >=  && x < width) {
                 //按照三角形绘制算法，我们需要判断某一点落在正确的一边就需要依赖三角形中的第三个点
                 //P1P2形成直线L1，判断（X， Y）是否落在正确的一边，就把P3和该点一起带入直线方程，同时大于0，或者同时小于0则为真（即有效）
                 //判断某一点是否对于三条直线方程都符合条件（都为真，则该点落在三角形内）
                 int ans1 = static_cast<int>(position[] - (position[] * k1 + b1));
                 int ans2 = static_cast<int>(y - (x * k1 + b1));
                 int ans3 = static_cast<int>(position[] - (position[] * k2 + b2));
                 int ans4 = static_cast<int>(y - (x * k2 + b2));
                 int ans5 = static_cast<int>(position[] - (position[] * k3 + b3));
                 int ans6 = static_cast<int>(y - (x * k3 + b3));
                 bool line1 = false, line2 = false, line3 = false;
                 if ((ans1 >  && ans2 >= -) || (ans1 <  && ans2 <= ))line1 = true;
                 if ((ans3 >  && ans4 >= -) || (ans3 <  && ans4 <= ))line2 = true;
                 if ((ans5 >  && ans6 >= -) || (ans5 <  && ans6 <= ))line3 = true;
                 if (line1 && line2 && line3) {
                     for (int z = ; z < spectrum; z ++){
                         if (solid) {
                             inputImage.atXYZC(x, y, , z) = static_cast<unsigned char>(color[z]);
                         }
                         else {
                             if (ans2 ==  || ans4 ==  ||ans6 == ) {
                                 inputImage.atXYZC(x, y, , z) = static_cast<unsigned char>(color[z]);
                             }
                         }
                     }
                 }

             }
         }
     }
 };

drawTri

　　

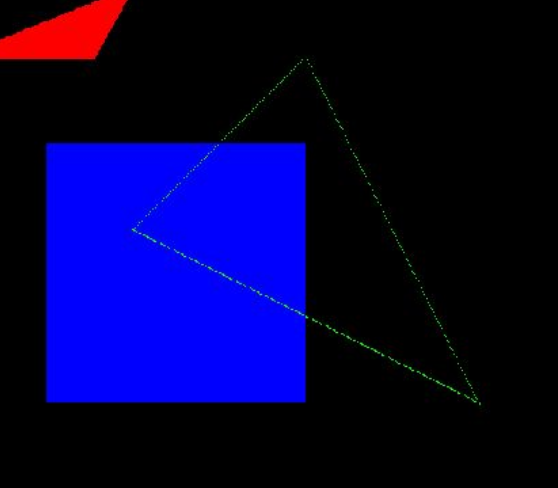
　　效果如下图：

　　（填充）

　　

　　（非填充）