【bzoj1005】[HNOI2008]明明的烦恼
1005: [HNOI2008]明明的烦恼
Time Limit: 1 Sec Memory Limit: 162 MB
Submit: 4175 Solved: 1660
[Submit][Status][Discuss]
Description
自从明明学了树的结构,就对奇怪的树产生了兴趣......给出标号为1到N的点,以及某些点最终的度数,允许在
任意两点间连线,可产生多少棵度数满足要求的树?
Input
第一行为N(0 < N < = 1000),
接下来N行,第i+1行给出第i个节点的度数Di,如果对度数不要求,则输入-1
Output
一个整数,表示不同的满足要求的树的个数,无解输出0
Sample Input
1
-1
-1
Sample Output
HINT
两棵树分别为1-2-3;1-3-2
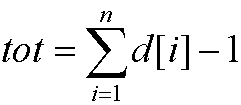
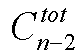 种插法;
种插法;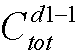 种插法;
种插法;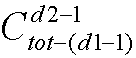 种插法;
种插法;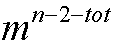 ;
;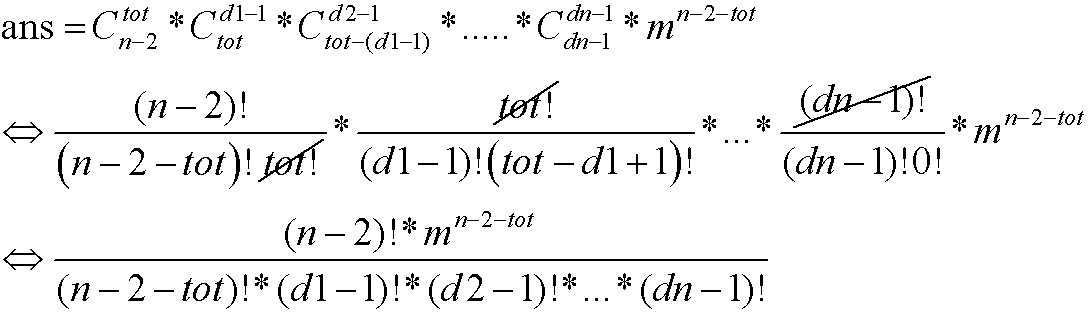
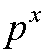 ,其中
,其中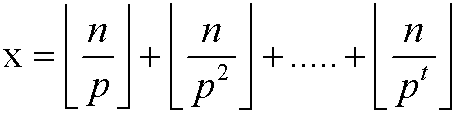 且
且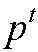 <n
<n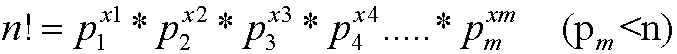
——转自怡红公子
#include<iostream>
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<cmath>
#include<ctime>
#include<algorithm>
using namespace std;
#define mod 1000000
int n,m,tot,cnt,len=,d[],pri[],num[],f[],ans[];
inline int read()
{
int x=,f=; char ch=getchar();
while(!isdigit(ch)) {if(ch=='-') f=-; ch=getchar();}
while(isdigit(ch)) {x=x*+ch-''; ch=getchar();}
return x*f;
}
void gets()//线性筛素数
{
memset(f,,sizeof(f));
for(int i=;i<=;i++)
{
if(f[i]) pri[++cnt]=i;
for(int j=;j<=cnt;j++)
{
if(pri[j]*i>)break;
f[pri[j]*i]=;
if(i%pri[j]==)break;
}
}
}
void solve(int x,int f)//暴力分解x
{
for(int i=;i<=x;i++)
{
int k=i;
for(int j=;j<=cnt;j++)
{
if(k<=) break;
while(k%pri[j]==)
{num[j]+=f; k/=pri[j];}
}
}
}
void mul(int x)//100万进制高精乘
{
for(int i=;i<=len;i++) ans[i]*=x;
for(int i=;i<=len;i++)
{
ans[i+]+=ans[i]/mod;
ans[i]%=mod;
}
while(ans[len+])
{len++; ans[len+]=ans[len]/mod; ans[len]%=mod;}
}
void print()//输出高精度数
{
for(int i=len;i;i--)
if(i==len) printf("%d",ans[i]);
else printf("%06d",ans[i]);
}
int main()
{
n=read(); ans[]=;
gets();//读素数表
if(n==) //特判
{
int x=read();
if(!x) printf("1\n");
else printf("0\n");
return ;
}
for(int i=;i<=n;i++)
{
d[i]=read();
if(!d[i]) {printf("0\n"); return ;}
if(d[i]==-) m++;
else d[i]--,tot+=d[i];
}
if(tot>n-) {printf("0\n"); return ;}
solve(n-,);
solve(n--tot,-);
for(int i=;i<=n;i++)
if(d[i]) solve(d[i],-);
for(int i=;i<=cnt;i++)
while(num[i]--)
mul(pri[i]);
for(int i=;i<=n--tot;i++)
mul(m);
print();
return ;
}
【bzoj1005】[HNOI2008]明明的烦恼的更多相关文章
- bzoj1005 [HNOI2008]明明的烦恼
1005: [HNOI2008]明明的烦恼 Time Limit: 1 Sec Memory Limit: 162 MBSubmit: 3032 Solved: 1209 Description ...
- bzoj1005: [HNOI2008]明明的烦恼(prufer+高精度)
1005: [HNOI2008]明明的烦恼 题目:传送门 题解: 毒瘤题啊天~ 其实思考的过程还是比较简单的... 首先当然还是要了解好prufer序列的基本性质啦 那么和1211大体一致,主要还是利 ...
- [BZOJ1005] [HNOI2008] 明明的烦恼 (prufer编码)
Description 自从明明学了树的结构,就对奇怪的树产生了兴趣......给出标号为1到N的点,以及某些点最终的度数,允许在任意两点间连线,可产生多少棵度数满足要求的树? Input 第一行为N ...
- 【prufer编码+组合数学】BZOJ1005 [HNOI2008]明明的烦恼
Description 自从明明学了树的结构,就对奇怪的树产生了兴趣...... 给出标号为1到N的点,以及某些点最终的度数,允许在任意两点间连线,可产生多少棵度数满足要求的树? Solution 这 ...
- BZOJ1005 HNOI2008明明的烦恼(prufer+高精度)
每个点的度数=prufer序列中的出现次数+1,所以即每次选一些位置放上某个点,答案即一堆组合数相乘.记一下每个因子的贡献分解一下质因数高精度乘起来即可. #include<iostream&g ...
- BZOJ1005:[HNOI2008]明明的烦恼(组合数学,Prufer)
Description 自从明明学了树的结构,就对奇怪的树产生了兴趣......给出标号为1到N的点,以及某些点最终的度数,允许在任意两点间连线,可产生多少棵度数满足要求的树? Input 第一行为N ...
- [bzoj1005][HNOI2008][明明的烦恼] (高精度+prufer定理)
Description 自从明明学了树的结构,就对奇怪的树产生了兴趣......给出标号为1到N的点,以及某些点最终的度数,允许在任意两点间连线,可产生多少棵度数满足要求的树? Input 第一行为N ...
- bzoj1005: [HNOI2008]明明的烦恼 prufer序列
https://www.lydsy.com/JudgeOnline/problem.php?id=1005 给出标号为1到N的点,以及某些点最终的度数,允许在任意两点间连线,可产生多少棵度数满足要求的 ...
- [bzoj1005][HNOI2008]明明的烦恼-Prufer编码+高精度
Brief Description 给出标号为1到N的点,以及某些点最终的度数,允许在 任意两点间连线,可产生多少棵度数满足要求的树? Algorithm Design 结论题. 首先可以参考这篇文章 ...
- [BZOJ1005][HNOI2008]明明的烦恼 数学+prufer序列+高精度
#include<cstdio> #include<cstring> #include<algorithm> using namespace std; int N; ...
随机推荐
- yii在TbGridView的td里面加入相应的下拉选项(转)
当你需要在一个GridView渲染某一个复杂元素的时候(特别是在这种情况下,这是一个小部件),这就需要你在控制器中调用一个动作.例如你给一个GridView的定义这样的一列: <?php $th ...
- .NET软件汉化小实例
Author:KillerLegend Date:2014.6.18 From:http://www.cnblogs.com/killerlegend/p/3795577.html 好的,今天我们来汉 ...
- .Net并行编程
1.什么是线程?线程和进程的区别是什么? 线程是程序执行的最小单元. 区别: 进程是操作系统进行资源处理和分配的最小单位,而一个进程可以包含多个线程,并共享进程的资源. 2.什么是多线程?为什么设计多 ...
- Python脚本控制的WebDriver 常用操作 <十> 层级定位
下面将使用WebDriver来模拟操作一个层级定位元素的操作 测试用例场景 在实际的项目测试中,经常会有这样的需求:页面上有很多个属性基本相同的元素,现在需要具体定位到其中的一个.由于属性基本相当,所 ...
- Map和HashMap
通过查询JDK帮助文档,我们可以得知Map的说明.方法等 import java.util.Map; import java.util.HashMap; class Test{ public stat ...
- Linux内核学习笔记——内核内存管理方式
一 页 内核把物理页作为内存管理的基本单位:内存管理单元(MMU)把虚拟地址转换为物理 地址,通常以页为单位进行处理.MMU以页大小为单位来管理系统中的也表. 32位系统:页大小4KB 64位系统:页 ...
- WebClient和HttpReuqest两种网络请求的方式
相对来说webClient请求的方式比较简单,可以直接通过new的方式创建一个实例,然后调用OpenReadAsync方法传进一个url,最后通过回调函数OpenReadCompleted就可以获取网 ...
- JavaScript高级程序设计之location对象
location对象用来处理URL的相关信息 1.获取查询字符串 // 获取查询字符串对象 var getQueryStringArgs = function () { ? location.sear ...
- libevent简介 构成
libevent简介 libevent是一个事件驱动的网络库,支持跨平台,如Linux, *BSD, MacOS X, Solaris, Windows.支持I/O多路复用,epoll.poll./d ...
- 条款10:令operator=返回一个*this的引用
为了编程的简洁性,有时候需要串联赋值,如:x = y = z = 15; 由于赋值采用右结合,因此上述语句被解释为:x = (y = (z = 15)); 为了实现串联赋值,复制操作符函数必须返回一个 ...
