机器学习-线性分类-支持向量机SVM-合页损失-SVM输出概率值-16
1. SVM概率化输出
标准的SVM进行预测 输出的结果是:

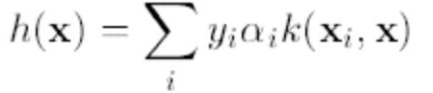
是无法输出0-1之间的 正样本 发生的概率值
sigmoid-fitting 方法:
将标准 SVM 的输出结果进行后处理,转换成后验概率
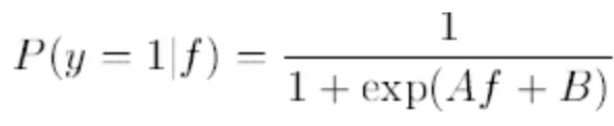
A,B 为待拟合的参数, f 为样本 x 的无阈值输出。
定义训练集为(fi,ti)

yi 为样本的所属类别,取值{-1,1}
利用之前的逻辑回归:
极小化训练集上的负对数似然函数
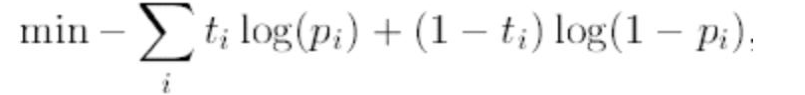
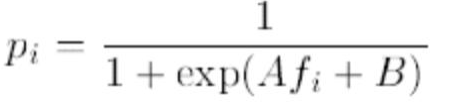
求出A和B,即可得到SVM的概率输出
import numpy as np
from sklearn.svm import SVC
X = np.array([[-1, -1], [-2, -1], [1, 1], [2, 1]])
y = np.array([1, 1, 2, 2])
cld = SVC(probability=True)
cld.fit(X, y)
print(cld.predict([[-0.8, -1]]))
print(cld.predict_proba([[-0.8, -1]]))
2. 合页损失
SVM某一条样本的损失

y(wx+b) >=1 分类正确 都没有损失
0<y(wx+b)<1 边界与超平面之间 有损失但是较小
y(wx+b)<0 彻底的分错了 loss=1+嵌入的深度
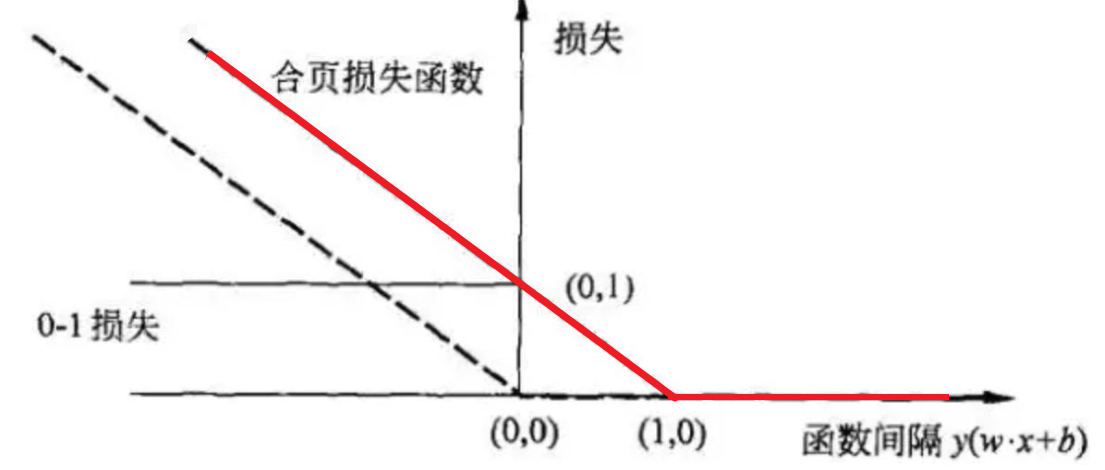
损失+正则项 得到目标函数:
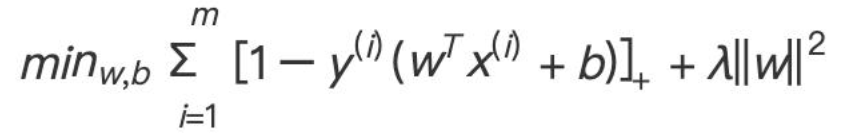
机器学习-线性分类-支持向量机SVM-合页损失-SVM输出概率值-16的更多相关文章
- 吴裕雄 python 机器学习——支持向量机线性分类LinearSVC模型
import numpy as np import matplotlib.pyplot as plt from sklearn import datasets, linear_model,svm fr ...
- 线性可分支持向量机与软间隔最大化--SVM(2)
线性可分支持向量机与软间隔最大化--SVM 给定线性可分的数据集 假设输入空间(特征向量)为,输出空间为. 输入 表示实例的特征向量,对应于输入空间的点: 输出 表示示例的类别. 我们说可以通过间隔最 ...
- 线性可分支持向量机--SVM(1)
线性可分支持向量机--SVM (1) 给定线性可分的数据集 假设输入空间(特征向量)为,输出空间为. 输入 表示实例的特征向量,对应于输入空间的点: 输出 表示示例的类别. 线性可分支持向量机的定义: ...
- svm 之 线性可分支持向量机
定义:给定线性可分训练数据集,通过间隔最大化或等价的求解凸二次规划问题学习获得分离超平面和分类决策函数,称为线性可分支持向量机. 目录: • 函数间隔 • 几何间隔 • 间隔最大化 • 对偶算法 1. ...
- 统计学习:线性可分支持向量机(SVM)
模型 超平面 我们称下面形式的集合为超平面 \[\begin{aligned} \{ \bm{x} | \bm{a}^{T} \bm{x} - b = 0 \} \end{aligned} \tag{ ...
- 简介支持向量机热门(认识SVM三位置)
支持向量机通俗导论(理解SVM的三层境地) 作者:July .致谢:pluskid.白石.JerryLead.出处:结构之法算法之道blog. 前言 动笔写这个支持向量机(support vector ...
- 支持向量机通俗导论(SVM学习)
1.了解SVM 支持向量机,因其英文名为support vector machine,故一般简称SVM,通俗来讲,它是一种二类分类模型,其基本模型定义为特征空间上的间隔最大的线性分类器,其学习策略便是 ...
- 支持向量机通俗导论 ——理解SVM的三层境界 总结
1.什么是支持向量机(SVM) 所谓支持向量机,顾名思义,分为两部分了解:一,什么是支持向量(简单来说,就是支持或支撑平面上把两类类别划分开来的超平面的向量点):二,这里的“机(machine,机器) ...
- Python实现鸢尾花数据集分类问题——基于skearn的SVM
Python实现鸢尾花数据集分类问题——基于skearn的SVM 代码如下: # !/usr/bin/env python # encoding: utf-8 __author__ = 'Xiaoli ...
- 机器学习理论基础学习3.3--- Linear classification 线性分类之logistic regression(基于经验风险最小化)
一.逻辑回归是什么? 1.逻辑回归 逻辑回归假设数据服从伯努利分布,通过极大化似然函数的方法,运用梯度下降来求解参数,来达到将数据二分类的目的. logistic回归也称为逻辑回归,与线性回归这样输出 ...
随机推荐
- offline RL | Pessimistic Bootstrapping (PBRL):在 Q 更新中惩罚 uncertainty,拉低 OOD Q value
论文题目:Pessimistic Bootstrapping for Uncertainty-Driven Offline Reinforcement Learning,ICLR 2022,6 6 8 ...
- 使用代码生成工具快速开发应用-结合后端Web API提供接口和前端页面快速生成,实现通用的业务编码规则管理
在前面随笔<在Winform应用中增加通用的业务编码规则生成>,我介绍了基于Winform和WPF的一个通用的业务编码规则的管理功能,本篇随笔介绍基于后端Web API接口,实现快速的Vu ...
- Windows手工入侵排查思路
文章来源公众号:Bypass Windows系统被入侵后,通常会导致系统资源占用过高.异常端口和进程.可疑的账号或文件等,给业务系统带来不稳定等诸多问题.一些病毒木马会随着计算机启动而启动并获取一定的 ...
- P5137 题解
前言 首先感谢所有帮助我卡常的大佬们. 题意 求 \((\sum_{i = 0}^{n} a^i b^{n - i})\mod p\) 的值(\(n \leq 10^{18}\),\(p\) 不一定为 ...
- flutter BLoC框架
BLoC(Business Logic Component)是一种在Flutter中用于管理状态和处理业务逻辑的设计模式和架构模式. BLoC 的核心思想是将应用程序的状态.业务逻辑和UI分离开来,以 ...
- Unity3D学习笔记5——创建子Mesh
目录 1. 概述 2. 详论 2.1. 实现 2.2. 解析 3. 参考 1. 概述 在文章Unity3D学习笔记4--创建Mesh高级接口通过高级API的方式创建了一个Mesh,里面还提到了一个Su ...
- RasaGPT对话系统的工作原理
RasaGPT 结合了 Rasa 和 Langchain 这 2 个开源项目,当超出 Rasa 现有意图(out_of_scope)的时候,就会执行 ActionGPTFallback,本质上就是利用 ...
- 【Pandas】groupby连用的count()和size()的区别
groupby连用的count()和size()的区别 count() 计算的是 value(数值): size() 计算的是 size(个数) 我们有以下表: size() age = df.gro ...
- 华为云媒体査勇:华为云在视频AI转码领域的技术实践
摘要:为大家介绍华为云媒体处理服务在视频AI转码领域的一些技术实践. 随着5G的落地和消费终端的不断升级,消费环节对视频画质的要求也越来越高,为了给消费者带来更清晰.更逼真和更具沉浸感的观感体验,对云 ...
- 一文了解如何使用移动应用安全组件Soot和Flowdroid
摘要:移动应用安全检测,soot.flowdroid分别作为静态分析.污点分析主要工具,能我们能够快速高效的进行检测分析.本文主要介绍两个工具的基本操作及相应的使用场景 本文分享自华为云社区<移 ...
