[模板]快速傅里叶变换(FFT)

Miskcoo大佬的多项式全家桶传送门

rvalue大佬的FFT讲解传送门

用途

将多项式快速(nlogn)变成点值表达，或将点值表达快速变回系数表达（逆变换），（多数时候）来达到求卷积的目的

做法

（为了方便，用w_n代表n次单位根的ω_n）

考虑选取特殊点，并用分治缩小问题规模

首先在多项式高位补零使其项数为2的幂，方便分治

然后我们选择代入单位根($w_n^k$)，设结果是$y_k$

首先有:$F(x)=\sum{a_ix^i}$

将$a_ix^i$按照幂次奇偶性分组，得到$F(x)=(a_0x^0+a_2x^2+...+a_{n-2}x^{n-2})+(a_1x^1+a_3x^3..a_{n-1}x^{n-1})$

然后设$F_0(x)=a_0x^0+a_2x^1+a_4x^2+...+a_{n-2}x^{\frac{n}{2}-1} $,$F_1(x)=a_1x^0+a_3x^1+a_5x^2+...+a_{n-1}x^{\frac{n}{2}-1}$

则$F(x)=F_0(x^2)+xF_1(x^2)$

于是现在我们将系数完成了分治，但需要代入的值的数量没变所以并没有什么卵用

现在带入n次单位根，$F(w^k_n)=F_0(w^{2k}_n)+w^k_nF_1(w^{2k}_n)$

然后单位根有一个比较喵喵的性质$w^{xk}_{xn}=w^k_n$

于是得到了$F(w^k_n)=F_0(w^k_{\frac{n}{2}})+w^k_nF_1(w^k_{\frac{n}{2}})$

还有一个更喵喵的性质$w^{k}_{n}=-w^{k+\frac{n}{2}}_n$

于是得到了$F(w^{k+\frac{n}{2}}_n)=F_0(w^k_{\frac{n}{2}})-w^k_nF_1(w^k_{\frac{n}{2}}) $

于是成功地完成了对代入的值的分治，可以递归来求了

然而递归太慢了，所以考虑怎么递推来做

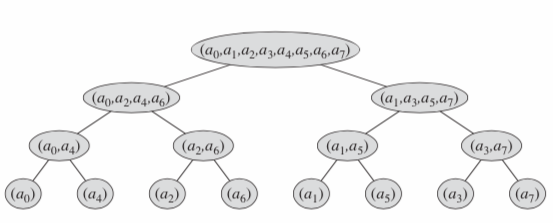　　　　（图是偷的）

我们可以从底向上做，将做出来的当前点的结果，用索引值加上这个节点的位置，存在一个大数组中（比如第三层{a₂,a₆}得出的两个结果存在A[2]和A[3]中，这个索引值可以根据现在在做的长度方便的计算出来）

这样的话，在我们向上推新的一层的时候，设旧一层长度为L，新一层所在节点的第一个编号为i，则有$A[i+k]=A[i+k]+w^k_{2L}A[i+L+k]，A[i+k+L]=A[i+k]-w^k_{2L}A[i+L+k] ,k=0..L-1$

然后我们只需要知道最底下一层元素的顺序就可以了

然后观察一下...发现一个很神奇的性质：最后一层第i个元素就对应a_rev[i]，其中rev[i]表示将i的二进制表示翻转后对应的数

原位置	0	1	2	3	4	5	6	7
原位置的二进制表示	000	001	010	011	100	101	110	111
重排后下标的二进制表示	000	100	010	110	001	101	011	111
重排结果	0	4	2	6	1	5	3	7

（表格也是偷的）

 

所以我们在读入系数后，直接把a_i的值给到A[rev[i]]就可以了

于是就得到了点值表达$\{(w^k_n，A[k])\}$

那么现在，只要再根据点值表达推回系数表达就行了

然后经过一系列神奇的推导（我反正不会），我们得到$a_j=\frac{1}{n}\sum_{k=0}^{n-1}y_kw_n^{-kj}$

它的形式和刚刚的定义十分类似，只有$w_n$的指数上多出了个负号，所以我们只要再把刚求出的$y_k$作为系数，把过程中的$w_n^k$改为$w_n^{-k}$，再做一次FFT，然后除以n就是最终结果

快速数论变换(NTT)

有的题要求取模，这时候复数的精度就比较爆炸

考虑在模一类特殊质数($a*2^k+1$，多为998244353)的情况下（任意模数我哪会啊）

可以发现原根(用g表示)和原来单位根的性质非常相似

于是我们用$g^{\frac{P-1}{n}}$代替$w_n$

关于原根怎么求..先记住998244353的原根是3吧233

实现

关于rev的求法：rev[i]=rev[i>>1]>>1|(i&1?(n>>1):0) n是长度

然后对于每个i<rev[i]，交换$a_i$和$a_{rev[i]}$ （为了防止交换两次）

可以预处理出所有$w_L^i$(或$g^{\frac{P-1}{L}i}$)，记到$g[i]$里（L是一个长度的上界）

然后用的时候，如果要用$w_n^k$，就可以直接用$g[L/n*k]$

随便上一个NTT的代码吧 FFT的效果差不多

 inline void fft(int *a,int n,bool flag){
     for(int i=;i<n;i++){
         rev[i]=(rev[i>>]>>)|((i&)?(n>>):);
         if(i<rev[i]) swap(a[i],a[rev[i]]);
     }
     for(int i=;i<=n;i<<=){
         int l=i>>;
         for(int j=;j<n;j+=i){
             for(int k=;k<l;k++){
                 int x=a[j+k],y=1ll*g[flag][L/i*k]*a[j+k+l]%P;
                 a[j+k]=(x+y)%P,a[j+k+l]=(x-y)%P;
             }
         }
     }
     if(flag){
         int in=fpow(n,P-);
         for(int i=;i<n;i++) a[i]=1ll*a[i]*in%P;
     }
 }

 inline void init{
     L=<<;
     g[][]=g[][]=,g[][]=fpow(,(P-)/L),g[][]=fpow(g[][],P-);
     for(int i=;i<L;i++) g[][i]=1ll*g[][i-]*g[][]%P,g[][i]=1ll*g[][i-]*g[][]%P;
 }