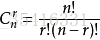逆元知识普及(进阶篇) ——from Judge

关于一些逆元知识的拓展

刚艹完一道 提高- 的黄题（曹冲养猪） ，于是又来混一波讲解了

　　——承接上文扫盲篇

 

---

四、Lucas定理(求大组合数取模)

 

题外话

这里Lucas定理的证明需要用到很多关于组合数的定理知识， 

那么关于一些组合数的知识，详情你可以看这里：Binamoto' blog。

再讲讲lucas定理这个东西(扩展lucas就不讲了,因为不大会…咳咳,然后也不怎么会用到吧)

基本公式： C(n,m) ≡ C(n/p,m/p)*C(n%p,m%p) (mod p)

    (也就是：   C(n,m)%p=C(n/p,m/p)*C(n%p,m%p)%p  )

适用范围：n 和 m 非常大，而模数 p 比较小的情况 (偷懒)

Lucas 定理的运用

将组合数中的 n 和 m 不断除以 p , 同时用除 p 的余数做组合数,累计入答案。
即,不断调用基本公式,递归求解,直至 m 等于 0 .
用上述例子就是：令C(n/p,m/p) ≡ C( (n/p)/p,(m/p)/p ) * C( (n/p)%p,(m/p)%p ) (mod p)
然后把 C(n/p,m/p) 求得的解 带入基本公式, 求出 C(n,m)%p 的值

证明及推导：

以下证明推导源自 Lucas定理——推导及证明

要证：C(n,m)%p=C(n/p,m/p)*C(n%p,m%p)%p
即证：C(n,m)=C(n/p,m/p)*C(n%p,m%p)
证明条件：已知p是素数，n、m、p为整数。

1.由二项式定理得：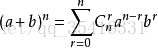 
 ，且 

2.由费马小定理得：
（1）式 ：$(x + 1) ^p ≡ x+1 (mod~ p)$ **[ 由x ^p ≡ x (mod p) , x 用 (x+1) 代替得到]**
（2）式 ：$x ^p + 1 ≡ x+1 (mod~ p)$ **[ 由x ^p ≡ x (mod p) , 等式两边同时+1得到]**

合并 1 、2 两式，得到：
（3）式 ：$(x + 1) ^p ≡ x ^p + 1 (mod~ p)$

3.由 $n = n/p *p + n\%p$ . 则：

$(x+1) ^p ≡ (x+1) ^{n/p *p} * (x+1)^{n\%p} (mod p)$
带入三式： $(x+1)^p ≡ (x^p +1)^{n/p}*(x+1)^{n\%p} (mod p)$

将上式由二项式公式可转化为：

$$\sum_{z=0}^n C_n^z ·x^z ≡ \sum_{i=0}^{n/p} C_{n/p}^i ~·~x^{p ~·~i} \sum_{j=0}^{n\%p} C_{n\%p}^j ·x^j \Big(mod ~~p \Big)$$

任意一个Z，必存在一个 i , j 满足：x ^ z = x ^ (p* i) * x^ j （即满足：n = n/p *p + n%p）， 
当且仅当： i=z/p，j=z%p 时成立 
此时, C(n,m)=C(n/p,m/p)*C(n%p,m%p) 成立 
证毕

相信这些东西你在看完后任然是懵逼的（me too）

那么你可以看看另外一个证明（来自可爱的 Binamoto ）：

设 $n=s*p+q,m=t*p+r(q,r<=p)$
我们要证 $C_{t*p+r}^{s*p+q} ≡C_{t}^{s} * C_{r}^{q} (modp)$
首先得有个前置知识，费马小定理 $x^p ≡ x (mod p)$
那么 $(x+1)^p ≡ x+1(mod p)$
且 $x^p+1 ≡ x+1 (mod p)$
所以 $(x+1)^p ≡ x^p+1 (mod p)$
然后 $(x+1)^n≡(x+1)^{s*p+q}$
$ ≡ ((x+1)^p)^{s} * (x+1)^q$
$ ≡ (x^p+1)^s * (x+1)^q ≡ (x^p+1)^s * (x+1)^q$
然后用二项式定理展开
≡$\sum_{i=0}^{s}C_{s}^{i}*x^{i*p} * \sum_{j=0}^{1}C_{q}^{j}*x^{j}$
总之就是 $(x+1)^p ≡ \sum_{i=0}^{s} C_{s}^{i} * x^{i*p} *\sum_{j=0}^{q} C_{q}^{j}*x^j$
然后考虑把两边的多项式展开一下
那么两边肯定都有 $x^{m}$ 即 $x^{t*p+r}$ 这一项（这是最上面的假设）
左边的 $x^m$ 的系数，根据上面的性质4推出来，应该是 $C_{n}^{m}$
然后右边嘞？只有 $i=t$ , $j=r$ 的时候才会有这一项，所以这一项的系数就是 $C_s^t * C_q^r$
然后又因为 $s=n/p$,$t=n%p$,$q=m/p$,$r=m%p$
然后就能证明: $$C(n,m) ≡ C(n/p,m/p) * C{n%p,m%p} (mod p)$$
然而万一 $q<r$ 该怎么办？那样的话 $j$ 根本不可能等于 $r$ 啊？

所以那样的话答案就是 $0$
因为上面乘上 $C{n%p,m%p}$ 答案就是 $0$
如何证明？

我们设 $f=n-m=z*q+x$
因为 $r>t$ , $x+r ≡ t (mod p)$
所以 $x+r=p+t$
又因为 $z*p+x+q*p+r = s*p+t$
所以 $z+q=s-1$
那么带进通项公式 $C_{n}^{m}= \dfrac{n!}{m! * f!}$ 之后，分子中有 $s$ 个 $p$ ，分母中有 $s-1$ 个 {p} ，
抵消之后分子中还有一个 $p$ ，那么这个数就是 $p$ 的倍数， $p$ 必然余 $0$.

Lucas 的代码(同上随意手打)：

//by Judge
define ll long long
ll mod;
inline ll quick_pow(ll x,ll p){
    ll ans=;
    while(p){
        if(p&) ans=ans*x%p;
        x=x*x%p, b>>=;
    }
    return ans;
}
inline ll C(ll n,ll m){
    ll cn=,cm=,res=;
    if(n<m) return ;
    if(n==m) return ;
    if(m>n-m) m=n-m;
    for(ll i=;i<m;++i){
        cn=(cn*(n-i))%mod;
        cm=(cm*(m-i))%mod;
    }
    res=(cn*quick_pow(cm,mod-))%mod;   //除法转换求逆元
    return res;
}
ll Lucas(ll n,ll m){
    ll ans=;
    while(n && m && ans){
        ans=(ans*C(n%mod,m%mod))%mod;   //拆分+递归
        n/=mod, m/=mod;
    }
    return ans;
}

 关于 Ex Lucas

这玩意儿别学了，要先会 CRT （可能是 exCRT？）的。

---

五、解线性同余方程组

其实这个玩意儿没什么高大上的，就CRT ... 什么的，你是没看过 NOI  day2 T1  吧，那个玩意儿...不说了，勾起了一些不美好的回忆（据说该题是所有题里面最简单的）

emmmm，首先解释一下这个东西。

线性同余方程组：

　　（ 求解 X ，其中 X  满足以下条件 ）

　　X≡b1 (mod a1)

　　X≡b2 (mod a2)

　　...

　　X≡bn (mod an)

 对，就和上面一样，是 n  个式子，（一般）让你求出 X  的最小正整数解（即满足 n 个式子的限制条件），这里看不大懂的话你可以看看曹冲养猪这道题，那个比喻也是蛮生动的

那么这玩意儿怎么解呢？ 别急，我们得先来看看 X  有解的条件。

其实条件很简单： b2 - b1  ≡  0 ( mod gcd(a1,a2) )

证明及推导：

　　设  X = a1 * x + b1 , 则 a1 * x + b1 ≡ b2 (mod a2)   （就是在式 2 中把 X 替换掉）

　　=> a1 * x ≡ b2 - b1 (mod a2) => a1 * x + a2 * y = b2 - b1  

　　那么和逆元有解条件的证明类似，只有  (b2-b1) | gcd(a1,a2)  时，原式有解（其中  (a) | (b)  代表 a 能被 b 整除 ）

　　证毕

 

所以呢？证明完了之后有什么用处么？ 当然有。

你看啊，上面的那个式子我们推着推着就退出来了一个方程对吧？是不是有点眼熟？ （提示一下 ax + by  ）

emmmm 对吧。就是类似一个扩欧的式子啊，因为 a1 和 a2 已知了啊。

然后我们用扩欧求出 a1*x + a2*y = gcd(a1,a2)   中 y1 的解就离胜利不远了

然后你看看我们解出来的这个 x 和 y  ，其实它并不是 a1 * x + a2 * y = b2 - b1   的解（这不显然嘛）

但是！ b2 - b1  是可以整除 gcd(a1,a2)  的（否则就是无解的情况），所以我们只需要让  x 和  y   乘以 (b2-b1)/gcd(a1,a2)  就可以令等式成立了

然后我们把 x  带入 X = a1 * x + b1  不就可以得到答案了？

同余方程的合并：

但是这里有个关键问题对吧（上面的这些推导只求出了 两个式子的解啊，我们不是要求满足n  个式子的解吗？）

所以我们要考虑的就是把这个方法延续下去...也就是说我们要把 1、2  两个式子合并起来，与第  3   个式子继续进行以上操作。

怎么合并？ =>   X=X' (mod lcm(a1,a2))   （其中 X'  是由前两个式子得到的答案，这里我们就是让 bi = X' ,  ai = lcm(a1,a2) ）

为什么可以这样合并？ 你只要知道 X'  是原式在 lcm(a1,a2)   范围内唯一的解就好了

（大家感性理解一下就好，我也不知道怎么证，已经颓废到懒得想了）

咳咳...简单解释一下：

 

　　你应该是知道在  a1 * x + a2 * y = b2 - b1   这个等式中的 x 和 y  的解释不止一种的（这个不知道我也没办法）

　　我们要改变着个解 就是 让 x  加上(减去) a2/d ，然后让 y 减去(加上) a1/d  ，等式依旧成立。（这里 d 表示 gcd(a1,a2) ，下同 ）

　　也就是说我们要用到的  x  可以加上或减去任意个 a2/d ，然后你看一下 ：  X = a1 * x + b1  ,

　　也就是说我们每次让  x  变化  ± a2  之后，X  的值就会加上或减去  a1 * a2/d  （即 X 可以加上任意个 lcm(a1,a2) ），

　　由此我们可以很容易看出：  X   在 lcm(a1 , a2)   范围内的解是唯一的。

 

所以两个式子就可以那样合并了...

还看不懂？woc 之前都白推了？emmm ，好吧，让我们看看之前的结论（过程结论）：

　　我们可以让  X   的值加上任意个  lcm(a1,a2)  

什么意思？ mod lcm(a1,a2)  = X  的意思啊！就是说任意一个数只要能 mod lcm(a1,a2)  =  X

所以这不就和之前那一堆式子 ： X ≡  bi  (mod ai)   一样了？ 推导完毕！

......

那么之后我们就反复迭代以上步骤，得到最终的答案

然后呢...没然后了啊，然后就是代码部分了啊QAQ

 

代码:

int ex_gcd(int a,int b,int& x,int& y){  //本来不想附 ex_gcd 代码来着的...
    if(!b) { x=,y=;return a; }
    int d=ex_gcd(b,a%b,y,x);
    y-=a/b*x; return d;
}
inline ll solv(int n){
    ll x=,m=; // x 记录前两个方程组的答案，初始为 0， m 记录前面所有的 a 的 lcm
    for(int i=;i<=n;++i){
        scanf("%lld%lld",&A,&B);
        ll b=B-x,d=ex_gcd(m,A,z,y);
        if (b%d!=) return -1ll;
        ll t=b/d*z%(A/d); x+=m*t,m*=A/d;
    } return x>0?x:x+m;
}

 

关于exCRT

 这东西别学了，烦的要命...

---

六、BSGS 定理 baby-step giant-step

BSGS的用处：

BSGS，魔鬼的步伐，怎么说呢...

有关BSGS的题目大多就是让你求 满足 $a^n ≡ 1 (mod\ p)$ 的最小的 n ，p 为质数

注意 p 为质数！否则就是 exBSGS

注意 n 是最小的，然后我们求出的 n 就是 a 模 p 意义下的阶

题外话：

这个东西很重要，为什么？因为 NTT 里面有用到原根...

原根是什么东西？原根就是：

对于一个数 a ，若其满足 a 在模 p 意义下的阶等于 p 的 φ 值（就是欧拉函数值），则 a 为 p 的阶

那么当 p 为质数时， φ 就为 p-1 咯。

小插曲：你知道大质数 998244353 怎么来的么？（不要告诉我你不知道这个模数）

其实它是从 NTT 中出来的，因为它的一个原根是 3 ，比较好记

另外，$998244353=7 * 17 * 2^23 + 1$

BSGS是什么：

讲了这么多没用的。。。我们回到原来的问题

原本的问题是： 让你求 满足 $a^n ≡ 1 (mod\ p)$ 的最小的 n

那么我们考虑分块，我们令  $a^n=a^{gt} \times a^h (mod\ p)$

其中 $t = \sqrt{p}$, g 、h 是未知数

那么 h 肯定是小于 t 的对吧？不然的话只要让 g 加上一，h就可以减去 t， 然后等式仍然成立

那么我们先考虑 g 的最大值是多少：

我们看看，a^p-1 是多少？ 明显是 1 吧？ 根据费马小定理来的，不证了

那么也就是说 p-1 是一个 a 的循环节，那么 g 的最大值就是 $\sqrt{p}$ 了

然后考虑一下我们只需要$O(\sqrt{p})$去枚举 g ，然后算出值存进map（或者hash表，更快）

然后原问题就可以转换为求找出是否存在 h ($h<=\sqrt{p}$) 使得 $a^{gt} \times a^h ≡ 1(mod\ p)$

然后移一下项就可以变成 $a^{gt} ≡ a^{-h}(mod\ p)$   ，其中 $a^{-h}$就是 $a^h$ 的逆元

然后再$O(\sqrt{p})$枚举 h ，算出 $a^{-h}(mod\ p)$ 然后看看 map 中有没有这个数，有的话 g*t+h 就是原等式的一个解了

其实不难吧？分块暴力嘛

（poj）

 inline void insert(int x,int y){ int k=x%mod;
     hs[++pat]=x,id[pat]=y,nxt[pat]=head[k],head[k]=pat;
 }
 inline int find(int x){  int k=x%mod;
     for(int i=head[k];i>=;i=nxt[i])
         if(hs[i]==x) return id[i]; return -;
 }
 inline int BSGS(int a,int b,int n){
     memset(head,-,sizeof(head));
     pat=; if(b==) return ;
     int m=sqrt(n+0.0),j; ll x=,p=;
     for(int i=;i<m;++i,p=p*a%n)
         insert((p*b%n),i);
     for(ll i=m;i<=n;i+=m)
         if((j=find(x=x*p%n))!=-) return i-j;
     return -;
 }

好了，Judge's Class  终于水完了，继续刷水题去   Bye~