第十五篇：使用 FP-growth 算法高效挖掘海量数据中的频繁项集

前言

对于如何发现一个数据集中的频繁项集，前文讲解的经典 Apriori 算法能够做到。

然而，对于每个潜在的频繁项，它都要检索一遍数据集，这是比较低效的。在实际的大数据应用中，这么做就更不好了。

本文将介绍一种专门检索频繁项集的新算法 - FP-growth 算法。它只会扫描数据集两次，能顺序挖掘出频繁项集。因此这种算法在网页信息处理中占据着非常重要的地位。

FP-growth 算法基本原理

将数据存储到一种成为 FP 树的数据结构中，这样的一棵树包含了数据集中满足最小支持度阈值的所有节点信息以及对应的支持度信息。

构建好了 FP 树之后，通过一定规则遍历这棵树就能挖掘出频繁项集。

PS：后面会专门讲解如何实现这样的一棵树，以及如何遍历这棵树。

FP 树

下图为 FP 树架构示意图：

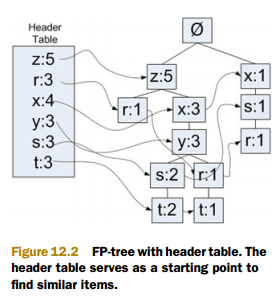
1. 右边部分中，"z:5" 的意思是，z在这条路径上出现了5次(包含其单个出现，也包含组合出现的情况)；

2. 顺着 "z:5" 往下，看到的是 r=1。这表示在这条路径上 "zr" 出现了一次；

3. 每个节点在树中都不是唯一的，比如能够清楚看到 r 出现了好几次；

4. 左边的部分，存放的是所有原子项出现的个数(包含其单个出现，也包含组合出现的情况)，同时它还 ”派生" 出一个链表将所有树结构部分中的相同原子项串起来；

5. 比如左边部分 r=3 就派生出一个链表串起了 3 个 r 节点，每个 r 节点标记都为1，故左边部分 r=3。

构建 FP 树

FP 树的机构稍微有点复杂，因此就不用字典，转用类(对象)来存树了。

下面是 FP 树结构的代码实现：

 class treeNode:
     'FP 树节点'

     #=====================================
     # 输入:
     #        nameValue: 节点名称
     #        numOccur: 节点路径出现次数
     #        parentNode: 父节点
     #=====================================
     def __init__(self, nameValue, numOccur, parentNode):
         '初始化函数'

         # 节点名字
         self.name = nameValue
         # 节点的路径出现次数
         self.count = numOccur
         # 指向相似节点
         self.nodeLink = None
         # 父节点
         self.parent = parentNode
         # 子节点
         self.children = {} 

     #=====================================
     # 输入:
     #        numOccur: 节点路径出现次数增量
     #=====================================
     def inc(self, numOccur):
         '增加节点出现次数'

         # 增加这个节点的路径出现次数
         self.count += numOccur

     #=====================================
     # 输入:
     #        ind: 节点路径出现次数增量
     #        ind: 子树序号
     #=====================================
     def disp(self, ind=1):
         '将树以文本形式显示'

         print '  '*ind, self.name, ' ', self.count
         for child in self.children.values():
             child.disp(ind+1)

以上代码定义的基本的 FP 树节点数据结构。接下来就是树生成部分以及表头(见上一部分图中左部)生成部分代码：

 def loadSimpDat():
     '载入测试数据'

     simpDat = [['r', 'z', 'h', 'j', 'p'],
                ['z', 'y', 'x', 'w', 'v', 'u', 't', 's'],
                ['z'],
                ['r', 'x', 'n', 'o', 's'],
                ['y', 'r', 'x', 'z', 'q', 't', 'p'],
                ['y', 'z', 'x', 'e', 'q', 's', 't', 'm']]
     return simpDat

 def createInitSet(dataSet):
     '将测试数据格式化为字典'

     retDict = {}
     for trans in dataSet:
         retDict[frozenset(trans)] = 0
     for trans in dataSet:
         retDict[frozenset(trans)] += 1
     return retDict

 #=====================================
 # 输入:
 #        dataSet: 数据集
 #        minSup: 最小支持度(实际为次数)
 # 输出:
 #        retTree: FP 树结构
 #        headerTable: 表结构
 #=====================================
 def createTree(dataSet, minSup=1):
     '创建 FP 树及其对应表结构'

     # 连续两次遍历数据集。第一次获取所有数据项及个数；第二次会支持度过滤。
     # 单元素频繁集(含出现次数)
     headerTable = {}
     for trans in dataSet:
         for item in trans:
             headerTable[item] = headerTable.get(item, 0) + dataSet[trans]
     for k in headerTable.keys():
         if headerTable[k] < minSup:
             del(headerTable[k])

     # 单元素频繁集(不含次数)
     freqItemSet = set(headerTable.keys())
     # 没有合乎要求的数据项则退出
     if len(freqItemSet) == 0:
         return None, None

     # 对表数据结构进行格式化，使之能够存放指针。
     for k in headerTable:
         headerTable[k] = [headerTable[k], None]

     # 新建初始化树节点
     retTree = treeNode('Null Set', 1, None)
     for tranSet, count in dataSet.items():

         # 当前事务的单元素集(含次数)
         localD = {}
         for item in tranSet:
             if item in freqItemSet:
                 localD[item] = headerTable[item][0]

         if len(localD) > 0:
             # 对localD中所有元素进行排序
             orderedItems = [v[0] for v in sorted(localD.items(), key=lambda p: p[1], reverse=True)]
             # 更新 FP 树
             updateTree(orderedItems, retTree, headerTable, count)

     # 返回FP树和表头结构
     return retTree, headerTable

 #=====================================
 # 输入:
 #        items: 事务项
 #        inTree: FP 树
 #        headerTable: 表结构
 #        count: 事务项的个数
 #=====================================
 def updateTree(items, inTree, headerTable, count):
     'FP 树生长函数'

     # 检查事务项中的第一个元素是否作为树的直接子节点存在
     if items[0] in inTree.children:
         # 存在则直接更新子树节点
         inTree.children[items[0]].inc(count)
     else:
         # 不存在则更新树结构
         inTree.children[items[0]] = treeNode(items[0], count, inTree)
         # 更新表结构
         if headerTable[items[0]][1] == None:
             headerTable[items[0]][1] = inTree.children[items[0]]
         else:
             updateHeader(headerTable[items[0]][1], inTree.children[items[0]])

     # 递归调用此树生长函数
     if len(items) > 1:
         updateTree(items[1::], inTree.children[items[0]], headerTable, count)

 #=====================================
 # 输入:
 #        nodeToTest: 指定表结构中的成员
 #        targetNode: 待加入链表节点的指针
 #=====================================
 def updateHeader(nodeToTest, targetNode):
     '表结构更新函数'

     while (nodeToTest.nodeLink != None):
         nodeToTest = nodeToTest.nodeLink

     nodeToTest.nodeLink = targetNode

 def main():
     'FP 树构建与展示'

     # 载入测试数据
     simpDat = loadSimpDat()
     # 将测试数据格式化为字典
     initSet = createInitSet(simpDat)
     # 创建 FP 树及对应表结构
     myFPTree, myHeaderTab = createTree(initSet, 3)
     # 展示 FP 树
     myFPTree.disp()

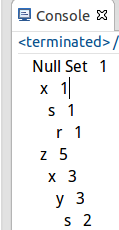
测试结果：

从 FP 树中挖掘频繁项集

FP 树构建好之后，就能对它进行挖掘，以找到所有频繁项集。

挖掘过程仅仅针对 FP 树和它对应的表结构，与原数据集没有任何关系了。

具体挖掘步骤如下：

1. 从 FP 树中获得条件模式基；

2. 利用条件模式基，获得一个条件 FP 树；

3. 迭代 1，2 直到树只剩下一个元素项。

下面分别讲解如何抽取条件模式基，以及如何从条件模式基构建 FP 树。

条件模式基的抽取

条件模式是指以所查找元素项为结尾的路径。

对于如下 FP 树来说：

r 的条件模式基为 {z}，{x，s}，{z，x，y} 。

而上图的左部表结构就是用来求取抽象基的一个辅助结构。通过每个子链表的每个节点都能向上迭代获取到一个路径，一个链表得到的所有路径和就是该链表元素项对应的条件模式基。

如下部分代码可用来求取元素项的条件模式基：

 #=====================================
 # 输入:
 #        leafNode: 表结构的子链表的节点
 #        prefixPath: 待返回路径
 #=====================================
 def ascendTree(leafNode, prefixPath):
     '获取FP树某个叶子节点的前缀路径'

     if leafNode.parent != None:
         prefixPath.append(leafNode.name)
         ascendTree(leafNode.parent, prefixPath)

 #=====================================
 # 输入:
 #        basePat: 元素项
 #        treeNode: 某个链表指向某首叶子节点的指针
 #=====================================
 def findPrefixPath(basePat, treeNode):
     '获取表结构中某个元素项的条件模式基'

     # 条件模式基
     condPats = {}

     # 获取某个元素项的条件模式基础并返回
     while treeNode != None:
         prefixPath = []
         ascendTree(treeNode, prefixPath)
         if len(prefixPath) > 1:
             condPats[frozenset(prefixPath[1:])] = treeNode.count
         treeNode = treeNode.nodeLink

     return condPats

条件 FP 树的构建与频繁项集的挖掘

对于每个频繁项，都要创建一个条件 FP 树。

条件 FP 树的创建代码，和之前的 FP 树是一样的。不过输入数据集会变成第一次求出的条件模式。

而且，第一次挖掘的仅仅是最小元素项，而后面挖掘出的频繁项都会基于上一步结果叠加。如此一直迭代下去直到表结构为空。

实现代码如下：

 #=====================================
 # 输入:
 #        inTree: 条件FP树
 #        headerTable: 条件表头结构
 #        minSup: 最小支持度
 #        preFix: 上一轮的频繁项
 #        freqItemList: 频繁项集
 #=====================================
 def mineTree(inTree, headerTable, minSup, preFix, freqItemList):
     '挖掘频繁项集'

     # 对表结构进行重排序(由小到大)
     bigL = [v[0] for v in sorted(headerTable.items(), key=lambda p: p[1])]

     # 遍历表结构
     for basePat in bigL:
         # 生成新频繁子项
         newFreqSet = preFix.copy()
         newFreqSet.add(basePat)
         # 加入频繁集
         freqItemList.append(newFreqSet)
         # 挖掘新的条件模式基
         condPattBases = findPrefixPath(basePat, headerTable[basePat][1])
         # 建立新的条件FP树
         myCondTree, myHead = createTree(condPattBases, minSup)
         # 若表结构非空，递归挖掘。
         if myHead != None:
             mineTree(myCondTree, myHead, minSup, newFreqSet, freqItemList)

测试结果：

小结

1. FP-growth 算法使用了新的数据结构，而且创建，遍历过程递归代码比较多，因此理解起来有点难度。

2. FP-growth 算法一般用来用来挖掘频繁项集，不用来学习关联规则。

3. 大数据领域中机器学习的部分就暂告一段落了(已学习完最为经典的算法)。接下来的精力将主要放在 Hadoop 云平台的使用及其底层机制实现部分。