编译原理-词法分析05-正则表达式到DFA-01

编译原理-词法分析05-正则表达式到DFA

要经历 正则表达式 --> NFA --> DFA 的过程。

0. 术语

Thompson构造Thompson Construction

利用ε-转换将正则表达式的机器片段“粘在一起”以构成与整个正则表达式相对应的机器。

ε-闭包ε-closure

可由ε-转换从某状态或某些状态达到的所有状态集合。

子集构造subset construction

通过ε-闭包将NFA构造为DFA的一种方法过程。

1. Thompson构造的基本表示

基本正则表达式

对于空转换

符号a的转换

并置

选择

重复

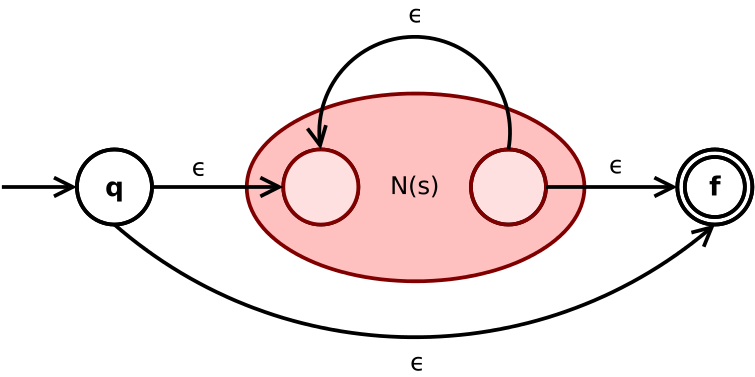
2. 示例

(ε|a*b)

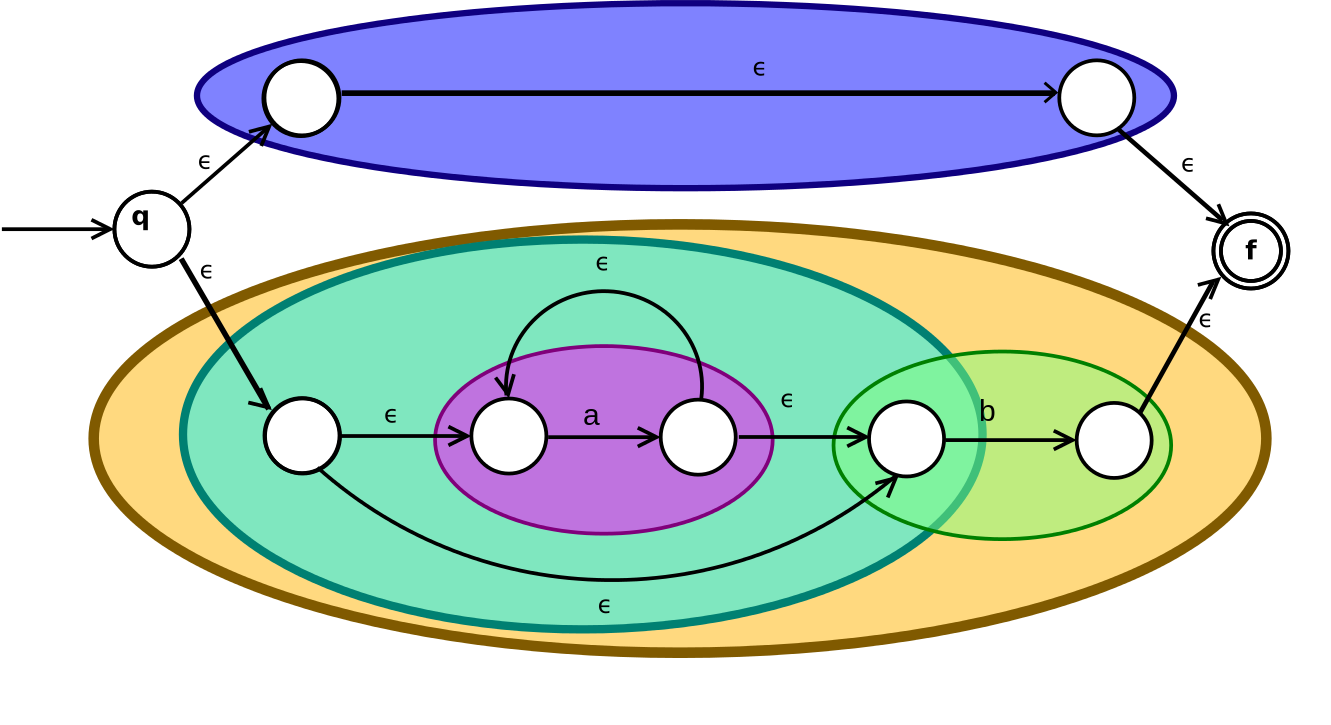
3. NFA2DFA——子集构造算法

input:NFA N

output：DFA D

计算字母表 ∑
计算NFA的开始状态的ε-闭包，作为 D 的初始状态，且未被标记。
while (在 D 中存在未被标记的状态 T)
{
　　取出T，为 T 加上标记  //出栈
   for (在∑中的每个字符a) //遍历字母表
   {
     states = move (T,a) // 从T经过字母a转换的状态集合
     U = ϵ-closure(states) //计算states的闭包
     if (U 不在 D 中) {
       将 U 加入 D 中，且未被标记  //新增一个状态，且转为的字符为a
     }
     T[a]=U  //记录转换
   }
}

ref: http://www.cnblogs.com/cyjb/p/LexerDfa.html

同样可以使用表驱动来完成构造过程。

NFA的状态集合	DFA上的状态	a	b	c