文本分类学习 （八）SVM 入门之线性分类器

SVM 和线性分类器是分不开的。因为SVM的核心：高维空间中，在线性可分（如果线性不可分那么就使用核函数转换为更高维从而变的线性可分）的数据集中寻找一个最优的超平面将数据集分隔开来。

所以要理解SVM首先要明白的就是线性可分和线性分类器。

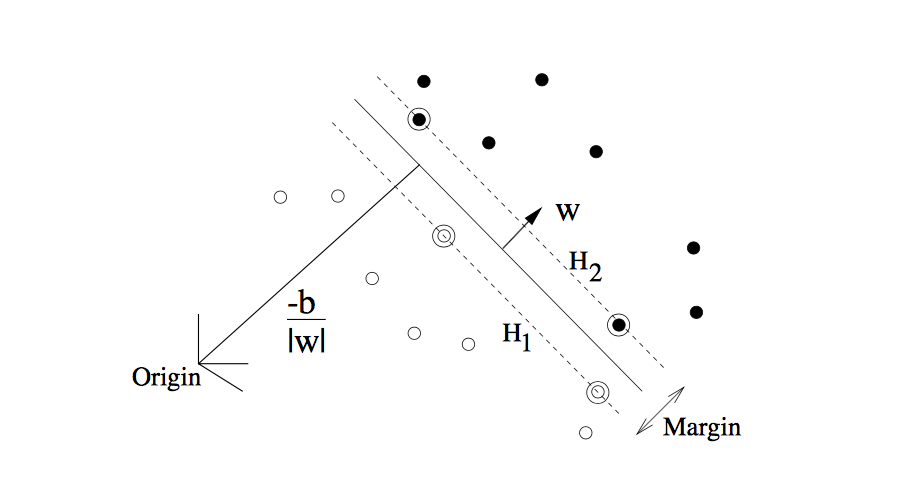
可以先解释这张图，通过这张图就可以了解线性分类器了。

这是一个在二维平面的图。其中实心点和空心点是分别属于两类的，Origin 是原点。

先看中间那条直线，中间的直线就是一条可以实心点和空心点分隔开来的直线，所以上图中的数据点是线性可分的。

这条直线其实就是线性分类器，也可以叫做分类函数，在直线上方的属于+1类，在直线下方的属于-1类。+1，-1这里只是区分类别。

所以该直线就是我们上面说的超平面，在二维空间中它是一条直线，三维空间是一个平面。。。等等，下面就统称为超平面

这个超平面上的点都满足

　　　　　　　　　　　　　　　　　　　　　　　　　　　　            （1）

这里需要解释一下：

• x 在二维平面中不是指横坐标值，而是指二维平面中点的向量，在文本分类中就是文本的向量表示。所以 x  = ( x_{i ,} y_i )
• w 也是一个向量 它是一个垂直于超平面的向量，如图中所示
• 该表达式不只是表示二维空间，也可以表示n维空间的超平面
• b 是一个常数
• w * x 是求两个向量的点积也就是内积，实际上应该写成w * x^T w乘以x的转置向量，w是横向量，x是列向量。

所以二维平面中，该表达式也可以表示为：

　　　　　　　　　　

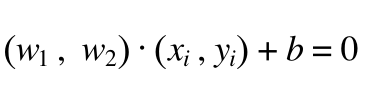　　　　　　　　　　　　　　　　　　　　    （2）

继续上图的解释，其中原点到超平面的距离为

　　　　　　　　　　　　　　　　　　　　　　　　 

这个可以很容易推导出来,以二维平面为例，上述表达式可以这么转换

　　　　　　　　　　　　　　　　　　　　

根据点到直线的距离公式：

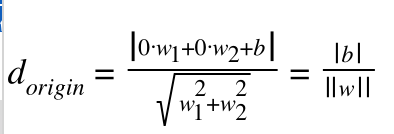　　             （3）

计算这个公式是为了方便我们下面计算得到几何间隔。

这里 || w || 叫做 向量 w 的 欧几里得范式，p维的向量w的范式：

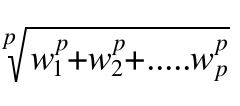
实际上是对向量长度的一种度量。

以上是在线性分类器中的一些要素：包括n维空间中的一些个点，和把这些点分开的一个超平面

下面是在SVM中对线性分类器不同的地方，在SVM中我们还要找到以下两条直线H₁, H₂ （上图已经是线性可分的最优分类线）

H₁  和 H₂ 它们平行于超平面，在H₁ 上的点满足：

        （4）

在H₂ 上的点满足：

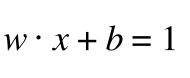        （5）

所以在图中我们可以看到空心点 都满足

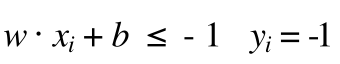   （6）

实心点都满足

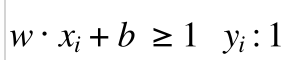     （7）

所以我们可以把上面连个式子写成一个不等式：

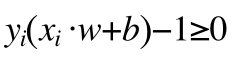        （8）

这个不等式就是图中所有数据点要满足的条件，也是最优分类函数求出来的条件。

这里还要提醒一下，x_i 不是横坐标而是一个n维向量，y_i 不是纵坐标而是一个分类标签，只有+1 和 -1。

上面计算过原点到超平面的距离，以此类推，H₁ 到原点的距离 =  |-1-b| / || w || ； H₂ 到原点的距离 = | 1 - b | / || w ||

那么H₁ 到超平面的距离就是 | b| / || w ||  -  |-1-b| / || w ||  = 1 / ||w|| 同理H₂到超平面的距离也是 1/ ||w||

H₁ 和H₂ 之间的距离为：2 / ||w|| 。这个距离称作为几何间隔。

SVM 的工作是在n维空间中找到这两个超平面：H₁ 和H₂ 使得点都分布在H₁ 和H₂ 的两侧，并且使H₁ 和H₂ 之间的几何间隔最大，这是H₁ 和H₂ 就是支持向量

为什么呢？因为几何间隔与样本的误分次数间存在关系, 几何间隔越大误分次数的上界就越小。

这个1/||w|| 也可以通过上面的不等式（8）推导出来，把不等式（8）左边和右边同时除以 || w ||

就可以得到:

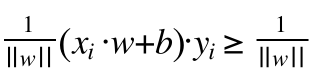         （9）

根据（6），（7）实际上y_i 只是一个正负号，相当于取绝对值，因为wx_i+b<=-1的时候y_i就是-1，结果还是正数，所以（9）可以变成：

    （10）

不等式左边表示的就是点到超平面wx+b=0的距离，该式子表示，所有点到超平面wx+b=0的距离都大于1/||w|| 。从图中看也正是如此。

所以我们接下来的工作就是最大化几何间隔，事实上也就是求||w||的最小值。