快速排序（Quick Sort）及优化

原理介绍

通过一趟排序将要排序的数据分割成独立的两部分，其中一部分的所有数据都比另外一部分的所有数据都要小，然后再按此方法对这两部分数据分别进行快速排序，整个排序过程可以递归进行，以此达到整个数据变成有序序列。

具体实现

左右指针法

• 实现说明

  

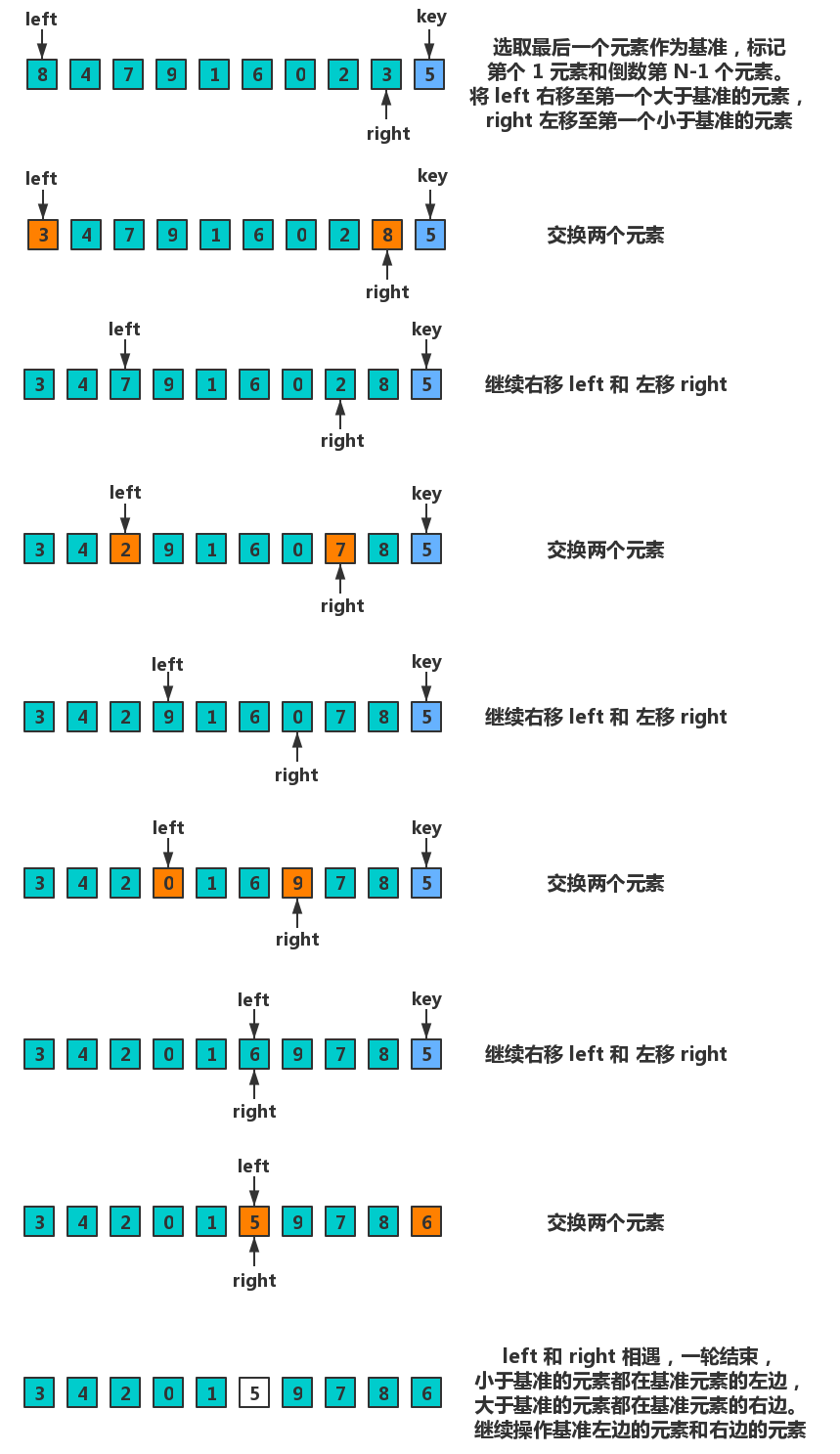
• 代码实现

    public static void sort1(int[] arr, int start, int end) {
        if (start >= end) {
            return;
        }
        int key = end;
        int left = start;
        int right = end - 1;
        int temp;
        //当left和right相遇时结束
        while (left < right) {
            //移动left至第一个大于基准的元素
            while (left < right && arr[left] <= arr[key]) {
                left++;
            }
            //移动right至第一个小于基准的元素
            while (left < right && arr[right] >= arr[key]) {
                right--;
            }
            //交换left和right元素
            temp = arr[left];
            arr[left] = arr[right];
            arr[right] = temp;
        }
        //交换相遇位置和基准
        if (arr[left] > arr[key]) {
            temp = arr[left];
            arr[left] = arr[key];
            arr[key] = temp;
        }
        //递归
        sort1(arr, start, left - 1);
        sort1(arr, right + 1, end);
    }
  

• 细节说明

  1. 下面的代码为什么还要判断left < right？

      while (left < right && arr[left] <= arr[key])
     

     key是序列的最后一个，right是key前一个位置，如果arr[right]=arr[key]，满足arr[left]<=arr[key]，然后left++，这时候left就会移动到key的位置

  2. 出了while循环并不是直接进行交换

      if (arr[left] > arr[key]) {
          temp = arr[left];
          arr[left] = arr[key];
          arr[key] = temp;
      }
     

     当left和right重合时，由于不满足left<right退出while循环不会继续右移left，若此时left元素依然小于基准元素则无需进行交换。

挖坑法

• 实现说明

  

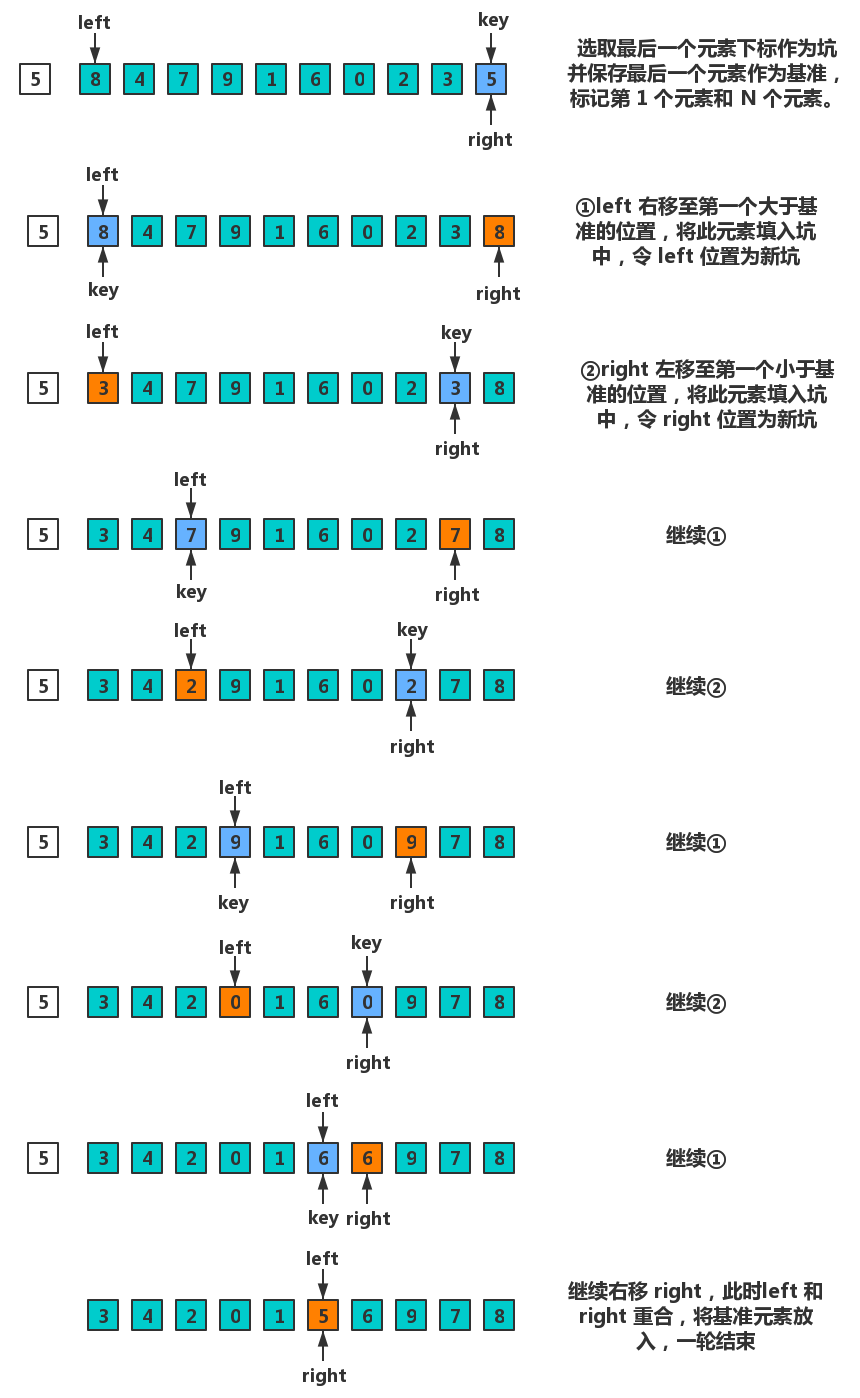
• 代码实现

    public static void sort2(int[] arr, int start, int end) {
        if (start >= end) {
            return;
        }
        int mark = arr[end];
        int left = start;
        int right = end;
        int key = end;
        //当left和right重合时结束
        while (left < right) {
            //left右移至第一个大于基准的位置
            while (left < right && arr[left] <= mark) {
                left++;
            }
            //将left元素填入坑中，令left位置为新坑
            arr[key] = arr[left];
            key = left;
            //right左移至第一个小于基准的位置
            while (left < right && arr[right] >= mark) {
                right--;
            }
            //将right元素填入坑中，令right位置为新坑
            arr[key] = arr[right];
            key = right;
        }
        //将基准元素放入重合位置
        arr[left] = mark;
        sort2(arr, start, left - 1);
        sort2(arr, right + 1, end);
    }
  

  由于坑位和right都为end，进行简化

    public static void sort3(int[] arr, int start, int end) {
        if (start >= end) {
            return;
        }
        int mark = arr[end];
        int left = start;
        int right = end;
        //当left和right重合时结束
        while (left < right) {
            //left右移至第一个大于基准的位置
            while (left < right && arr[left] <= mark) {
                left++;
            }
            //将left元素填入坑中，令left位置为新坑
            arr[right] = arr[left];
            //right左移至第一个小于基准的位置
            while (left < right && arr[right] >= mark) {
                right--;
            }
            //将right元素填入坑中，令right位置为新坑
            arr[left] = arr[right];
        }
        //将基准元素放入重合位置
        arr[left] = mark;
        sort2(arr, start, left - 1);
        sort2(arr, right + 1, end);
    }
  

前后指针法

• 实现说明

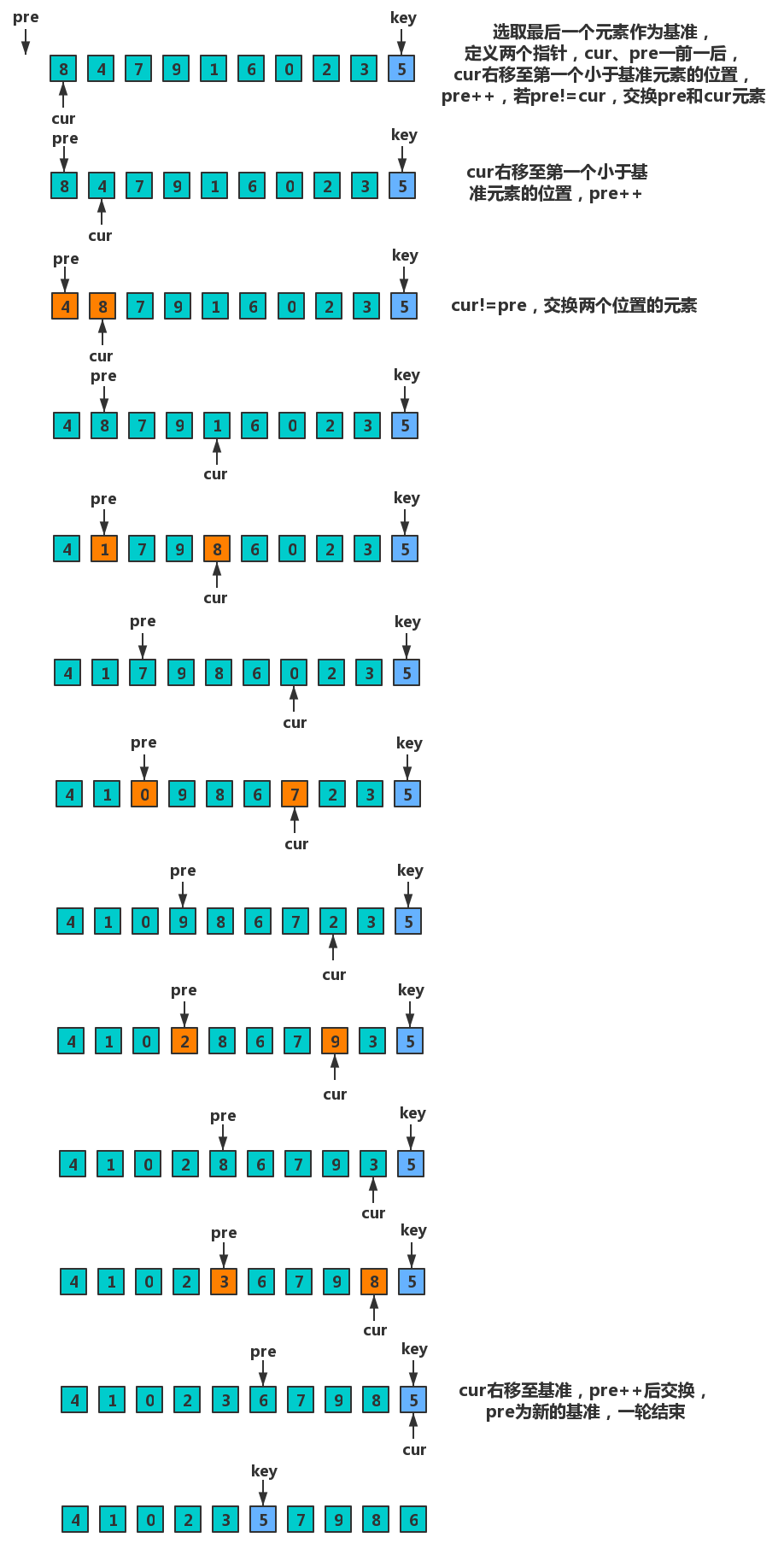
• 代码实现

    public static void sort4(int[] arr, int start, int end){
        if (start >= end) {
            return;
        }
        int key = end;
        int cur = start;
        int pre = cur - 1;
        int temp;
        //结束循环时cur在基准处
        while (cur < key) {
            //当cur元素小于基准元素时才会pre++
            if (arr[cur] < arr[key] && ++pre != cur) {
                temp = arr[cur];
                arr[cur] = arr[pre];
                arr[pre] = temp;
            }
            cur++;
        }
        temp = arr[cur];
        arr[cur] = arr[++pre];
        arr[pre] = temp;
        sort4(arr, start, pre - 1);
        sort4(arr, pre + 1, end);
    }
  

优化方案

三数取中

选用待排数组最左边、最右边和最中间的三个元素的中间值作为基准

随机选取基准

在待排序列是部分有序时，固定选取枢轴使快排效率底下，要缓解这种情况，就引入了随机选取枢轴

根据分区大小调整算法

当分区的规模达到一定小时，停止快速排序算法，使用选择排序等算法

相同元素相聚

在一次分割结束后，可以把与Key相等的元素聚在一起，继续下次分割时，不用再对与key相等元素分割

1. 在划分过程中，把与key相等元素放入数组的两端

2. 划分结束后，把与key相等的元素移到基准周围