BZOJ3004: 吊灯(结论 毒瘤)

题意

$n$个节点的树，判断能否划分成$\frac{n}{k}$个大小为$k$的联通块

Sol

首先$k$必须是$n$的倍数。

然后刚开始我就非常傻的以为输出所有约数就行了。。

但是图是这样，$k = 2$的话肯定是不行的。

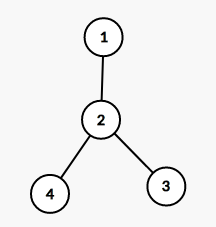
结论：若$k$是可行的，则至少有$\frac{n}{k}$个节点的大小为$k$的倍数

证明：直接归纳吧。

$k = n$的时候显然

$k = n / 2$的时候，我们要把树划分成互不相交的两块，这两块一定是完全独立的，且分别有自己的根节点。

剩下的继续归纳即可，注意这里我们为什么要是“至少”，因为整棵树是联通起来的，我们在判断$k$的时候，大小为$2k$的也会被统计入答案

然后这题卡dfs，不愧是SDOI。。

#include<cstdio>
#include<algorithm>
#include<vector>
#include<cstring>
using namespace std;
const int MAXN =  * 1e6;
inline int read() {
    char c = getchar(); int x = , f = ;
    while(c < '' || c > '') {if(c == '-') f = -; c = getchar();}
    while(c >= '' && c <= '') x = x *  + c - '', c = getchar();
    return x * f;
}
int N;
vector<int> ap;
int fa[MAXN], tim[MAXN];
void rebuild() {
    memset(tim, , sizeof(tim));
   // for(int i = 1; i <= N; i++) v[i].clear();
    for(int i = ; i <= N; i++) fa[i] = (fa[i] + ) % (i - ) + ;
}
int siz[MAXN];
/*void dfs(int x, int fa) { mdzz卡dfs，不愧是SDOI啊。。
    siz[x] = 1;
    for(int i = 0; i < v[x].size(); i++) {
        int to = v[x][i];
        if(to == fa) continue;
        dfs(to, x);
        siz[x] += siz[to];
    }
}*/
void solve(int id) {
    printf("Case #%d:\n", id);
    for(int i = ; i <= N; i++) siz[i] = ;
    for(int i = N; i >= ; i--) siz[fa[i]] += siz[i];
    for(int i = ; i <= N; i++) tim[siz[i]]++;
    for(int i = ; i < ap.size(); i++) {
        int num = ap[i], cnt = ;
        for(int j = num; j <= N; j += num)
            cnt += tim[j];
        if(cnt >= N / num) {
            printf("%d\n", num);
        }
    }
}
int main() {
    N = read();
    for(int i = ; i <= N; i++)
        if(N % i == )
            ap.push_back(i);
    for(int i = ; i <= N; i++)
        fa[i] = read();
    solve();
    for(int i = ; i <= ; i++) {
        rebuild();
        solve(i);
    }
    return ;
}