luogu P2831 愤怒的小鸟

题目描述

Kiana最近沉迷于一款神奇的游戏无法自拔。

简单来说，这款游戏是在一个平面上进行的。

有一架弹弓位于(0,0)处，每次Kiana可以用它向第一象限发射一只红色的小鸟，小鸟们的飞行轨迹均为形如y=ax^2+bxy=ax

2

+bx的曲线，其中a,b是Kiana指定的参数，且必须满足a<0。

当小鸟落回地面(即x轴）时，它就会瞬间消失。

在游戏的某个关卡里，平面的第一象限中有n只绿色的小猪，其中第i只小猪所在的坐标为(xi,yi)。

如果某只小鸟的飞行轨迹经过了(xi,yi),那么第i只小猪就会被消灭掉，同时小鸟将会沿着原先的轨迹继续飞行；

如果一只小鸟的飞行轨迹没有经过(xi,yi)，那么这只小鸟飞行的全过程就不会对第i只小猪产生任何影响。

例如，若两只小猪分别位于(1,3)和(3,3)，Kiana可以选择发射一只飞行轨迹为y=-x^2+4xy=−x

2

+4x的小鸟，这样两只小猪就会被这只小鸟一起消灭。

而这个游戏的目的，就是通过发射小鸟消灭所有的小猪。

这款神奇游戏的每个关卡对Kiana来说都很难，所以Kiana还输入了一些神秘的指令，使得自己能更轻松地完成这个游戏。这些指令将在【输入格式】中详述。

假设这款游戏一共有T个关卡，现在Kiana想知道，对于每一个关卡，至少需要发射多少只小鸟才能消灭所有的小猪。由于她不会算，所以希望由你告诉她。

输入输出格式

输入格式：

第一行包含一个正整数T，表示游戏的关卡总数。

下面依次输入这T个关卡的信息。每个关卡第一行包含两个非负整数n,m，分别表示该关卡中的小猪数量和Kiana输入的神秘指令类型。接下来的n行中，第i行包含两个正实数(xi,yi)，表示第i只小猪坐标为(xi,yi)。数据保证同一个关卡中不存在两只坐标完全相同的小猪。

如果m=0，表示Kiana输入了一个没有任何作用的指令。

如果m=1，则这个关卡将会满足：至多用\left \lceil \frac{n}{3} + 1 \right \rceil⌈

3

n

​ +1⌉只小鸟即可消灭所有小猪。

如果m=2,则这个关卡将会满足：一定存在一种最优解，其中有一只小鸟消灭了至少\left \lfloor \frac{n}{3} \right \rfloor⌊

3

n

​ ⌋只小猪。

保证1<=n<=18，0<=m<=2，0<xi,yi<10，输入中的实数均保留到小数点后两位。

上文中，符号\left \lceil x \right \rceil⌈x⌉和\left \lfloor x \right \rfloor⌊x⌋分别表示对c向上取整和向下取整

输出格式：

对每个关卡依次输出一行答案。

输出的每一行包含一个正整数，表示相应的关卡中，消灭所有小猪最少需要的小鸟数量

输入样例#1：
```
2
2 0
1.00 3.00
3.00 3.00
5 2
1.00 5.00
2.00 8.00
3.00 9.00
4.00 8.00
5.00 5.00
```
输出样例#1： 复制
```
1
1
```
输入样例#2： 复制
```
3
2 0
1.41 2.00
1.73 3.00
3 0
1.11 1.41
2.34 1.79
2.98 1.49
5 0
2.72 2.72
2.72 3.14
3.14 2.72
3.14 3.14
5.00 5.00
```
输出样例#2： 复制
```
2
2
3
```
输入样例#3： 复制
```
1
10 0
7.16 6.28
2.02 0.38
8.33 7.78
7.68 2.09
7.46 7.86
5.77 7.44
8.24 6.72
4.42 5.11
5.42 7.79
8.15 4.99
```
输出样例#3： 复制
```
6
```
##说明

【样例解释1】

这组数据中一共有两个关卡。

第一个关卡与【问题描述】中的情形相同，2只小猪分别位于（1.00,3.00)和 (3.00,3.00)，只需发射一只飞行轨迹为y = -x^2 + 4x的小鸟即可消灭它们。

第二个关卡中有5只小猪，但经过观察我们可以发现它们的坐标都在抛物线 y = -x^2 + 6x上，故Kiana只需要发射一只小鸟即可消灭所有小猪。

【数据范围】

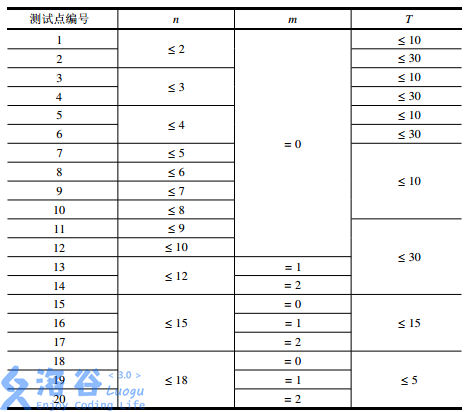
就是一道装压dp,二进制表示小猪存过情况具体看注释

#include<cmath>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define eps 1e-12
#define INF 0x3f3f3f3f
const int maxn = 100007;
double x[maxn],y[maxn];
int T,n,spj;
int can[21][21],dp[1<<20];
bool judge(double a,double b) {
	return fabs(a-b)<=eps;    //精度
}
void CCL () {
	memset(can,0,sizeof can);
	memset(dp,0x3f,sizeof dp);
}
int main () {
	scanf("%d",&T);
	while(T--)
	{

		scanf("%d%d",&n,&spj);CCL();
		for(int i=1;i<=n;++i)
			scanf("%lf%lf",x+i,y+i);
		for (int i=1;i<n;++i)
			for (int j=i+1;j<=n;++j)
			{
				if(judge(x[i],x[j]))continue;
				double a=((y[i]/x[i])-(y[j]/x[j]))/(x[i]-x[j]);
				if(a>=0)continue;//下凸二次函数
				double b=y[i]/x[i]-a*x[i];
				for(int k=1;k<=n;++k)
					if(judge(a*x[k]+b,y[k]/x[k]))		//若满足ax^2+bx=y --> 则ax+b=y/x;
						can[i][j]|=(1<<(k-1));//把第k位上变为1
			}
		dp[0]=0;
		int k = (1<<n)-1;
		for (int i=0;i <= k;++i)
		{
			for (int j=1;j <= n;++j)
			{
				if(!(i&(1<<(j-1)))) //抛物线i打不掉猪j
				{
					for(int k=j;k<=n;k++)  { //前面的都打过了
						if(k==j) {
							dp[i|(1<<(j-1))]=std::min(dp[i|(1<<(j-1))],dp[i]+1);
							continue;
						}
						if(judge(x[k],x[j])) continue; //横坐标相同，一次打不掉
						dp[i|can[j][k]]=std::min(dp[i|can[j][k]],dp[i]+1);//找到一只可以打猪j，k的抛物线
					}
					break;
				}
			}
		}
		printf("%d\n",dp[k]);
	}
}