Acwing 883高斯消元法的运用

Acwing 883高斯消元法的运用

解线性方程组

Acwing 883

输入一个包含 n 个方程 n 个未知数的线性方程组。

方程组中的系数为实数。

求解这个方程组。

下图为一个包含 m 个方程 n 个未知数的线性方程组示例：

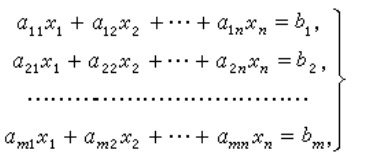
输入格式

第一行包含整数 n。

接下来 n 行，每行包含 n+1 个实数，表示一个方程的 n 个系数以及等号右侧的常数。

输出格式

如果给定线性方程组存在唯一解，则输出共 n 行，其中第 i 行输出第 i 个未知数的解，结果保留两位小数。

如果给定线性方程组存在无数解，则输出<Infinite group solutions>。

如果给定线性方程组无解，则输出 <No solution>。

数据范围

1≤n≤100,

所有输入系数以及常数均保留两位小数，绝对值均不超过 100。

输入样例：

3
1.00 2.00 -1.00 -6.00
2.00 1.00 -3.00 -9.00
-1.00 -1.00 2.00 7.00

输出样例：

1.00
-2.00
3.00

Train of thought

根据线性代数高斯消元求解线性方程组的方法：

从每一列的角度考虑，先找出每一列中绝对值最大的数

然后把这个数所对应行与对应要处理的行交换，我们要做的就是尽可能地将它化为阶梯型矩阵

如：按照样例来分析

所对应的增广矩阵变化为

现在我们的任务是处理第一行，将第一行第一列归一以后把下面每行第一个数消掉

所以原矩阵变为

可以看到第一列的任务已经完成了，下面开始处理第二行，后面的思路以此类推

最后应化为上三角矩阵

Note:

• 由于最后处理完是上三角矩阵，如果是有解的，我们还要从最后一行来进行向上的消元，这样才能得到每一个元素的解
• 由于计算机浮点数的不精确度，我们需要定义一个浮点数常量来判断当前的数是否为0，在本题中可以设为1e-6
• 如果判断出当前的那一列最大的数为0；应该直接循环下一列，而待处理的行不发生改变；
• 判断无解的情况即0 = bi,而bi通过计算不为0；

综上所述，代码如下：

#include<iostream>
#include<iomanip>
#include<cmath>
using namespace std;
double Matrix[105][105];
int n;
double Exp = 1e-6;
int guass()
{
    int c,r;
    for(c = 1,r = 1; c <= n; ++c)
    {
        int p = r;
        for(int t = r; t <= n; ++t)
            if(fabs(Matrix[t][c]) > fabs(Matrix[p][c]))
            p = t;//找到绝对值最大的数所对应的行
        if(fabs(Matrix[p][c]) < Exp) continue;//这里对应第三点注意
        for(int i = c; i <= n + 1; ++i) swap(Matrix[p][i], Matrix[r][i]);
        for(int i = n + 1; i >= c; --i) Matrix[r][i] /= Matrix[r][c];//第一个系数归一
        for(int i = r + 1; i <= n; ++i)
        for(int j = n + 1; j >= c; --j)
        if(fabs(Matrix[i][c] )> Exp)
        Matrix[i][j] -= Matrix[i][c] * Matrix[r][j];//消元
        r++;
    }
    if(r <= n)
    {
        for(int i = r; i <= n; ++i)
        if(fabs(Matrix[i][n + 1]) > Exp)
        return 1;//对应第4点注意
        return 2;
    }
   for (int i = n  ; i >= 1; i -- )
        for (int j = i - 1; j >= 1; j -- )
            Matrix[j][n + 1] -= Matrix[j][i] * Matrix[i][n + 1];
    return 0;
}
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    cin >> n;
    for(int i = 1; i <= n; ++i)
    for(int j = 1; j <= n + 1; ++j)
    cin >> Matrix[i][j];
    int t = guass();
    cout << setprecision(2) <<fixed;
    if(t == 0)
        for(int i = 1; i <= n; ++i)
            cout << Matrix[i][n + 1] << endl;
    else if(t == 1)
        cout << "No solution" << endl;
    else
        cout << "Infinite group solutions" << endl;
    return 0;
}

感谢大家的阅读，第一次写博客，有些地方做的不好的恳请大家指出，一定会多加改进(￣▽￣)