Proximal Algorithms 1 介绍

目录

• 定义
• 解释
  • 图形解释
  • 梯度解释
• 一个简单的例子

Proximal Algorithms

定义

令\(f: \mathrm{R}^n \rightarrow \mathrm{R} \cup \{+ \infty \}\)为闭的凸函数，即其上镜图:

\[\mathbf{epi} f = \{ (x, t) \in \mathrm{R}^n \times \mathrm{R}| f(x) \le t\}
\]

为非空闭的凸集，定义域：

\[\mathbf{dom} f = \{x \in \mathrm{R}^n| f(x) < + \infty\}
\]

近端算子(是这么翻译的?)proximal operator \(\mathbf{prox}_f: \mathrm{R}^n \rightarrow \mathrm{R}^n\)定义为：



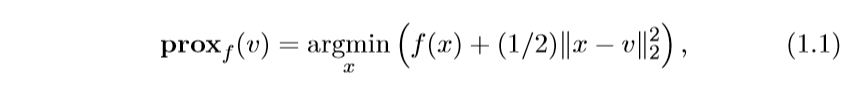
我们常常会对添加一个比例系数\(\lambda\)，而关心\(\lambda f\)的近端算子：



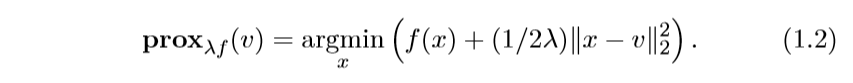
注：等式右边乘以一个常数\(\lambda\)便是\(\lambda f\)的形式，所以是等价的。

解释

图形解释

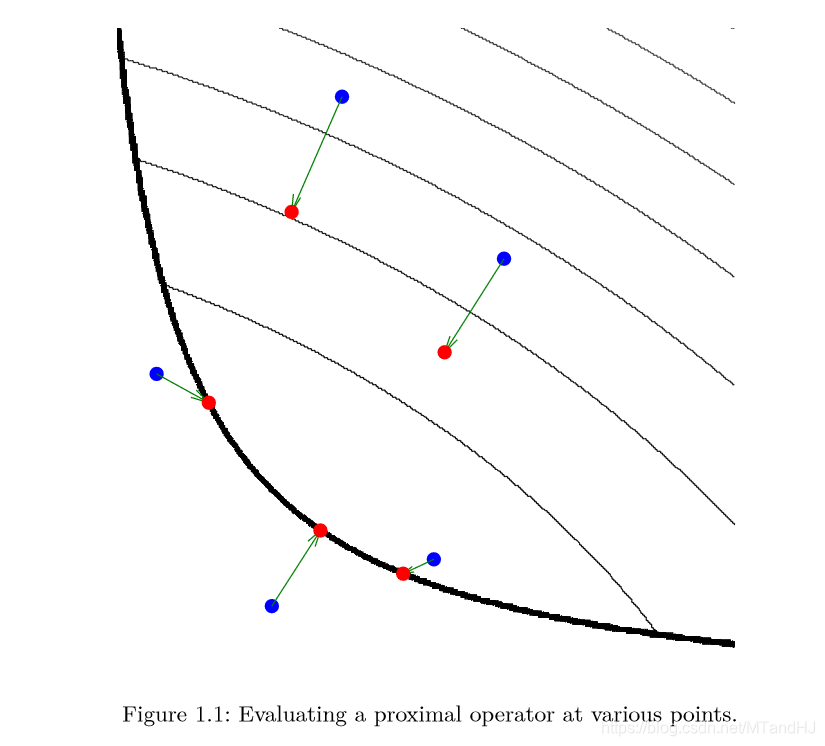
注：图中的细黑线是函数\(f\)的等值线，而粗黑线表示定义域的边界。在蓝色的点处估计其\(\mathbf{prox}_f\)得到红色的点。

可以发现，\(\mathbf{prox}_f(v)\)实际上是对点\(v\)附近的一个估计。

梯度解释

假设\(\lambda\)很小，且\(f\)可微，那么，容易知道\(f(x) + \frac{1}{2\lambda}\|x-v\|_2^2\)取得极值(实际上也是最值)的条件是：

\[\nabla f(x) +\frac{x-v}{\lambda}=0 \Rightarrow x=v-\lambda \nabla f(x) \approx v-\lambda \nabla f(v)
\]

可以看到，\(\mathbf{prox}_f(v)\)近似为在\(v\)点的梯度下降，而\(\lambda\)为步长。

一个简单的例子

有一个问题，就是，如果我们的目的是最小化\(f(x)\)，那么利用\(\mathbf{prox}_f\)会不会太愚蠢了，既然我们能求解\(\mathbf{prox}_f\)，那么直接最小化\(f(x)\)应该也不是难事吧。这个问题留到以后再讨论吧，我也不知道能否找到一个恰当的例子来反驳。

当\(f\)是一个示性函数：



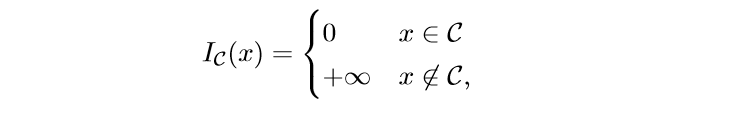
其中\(\mathcal{C}\)为非空凸集，我们来看看这个时候的\(\mathbf{prox}_f(v)\):

\[\mathbf{prox}_{\lambda f}(v)= \mathrm{argmin}_x \: I_{\mathcal{C}}(x) + \frac{1}{2 \lambda}\|x-v\|_2^2
\]

首先，我们可以确定\(x \in \mathcal{C}\), 否则结果为无穷，所以，问题可以转化为一个Euclid范数下投影问题：



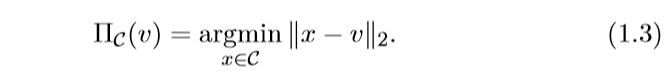
所以一个问题是，如果\(\mathbf{prox}_f\)的尾项不用\(\ell_2\)范数，用别的范数会变成什么样？