[Noip 2018][标题统计 龙湖斗 摆渡车 对称二叉树]普及组题解

啊喂，都已经9102年了，你还在想去年？

这里是一个Noip2018年PJ第二题打爆的OIer，错失省一

但经过了一年，我学到了很多，也有了很多朋友，水平也提高了很多，现在回看当时：

今年的Noip CSP也快要开始了,想在这里写下这篇题解，仅以此篇献给当时的自己和以后的OI路。

---

正文开始：

T1：标题统计

题面：

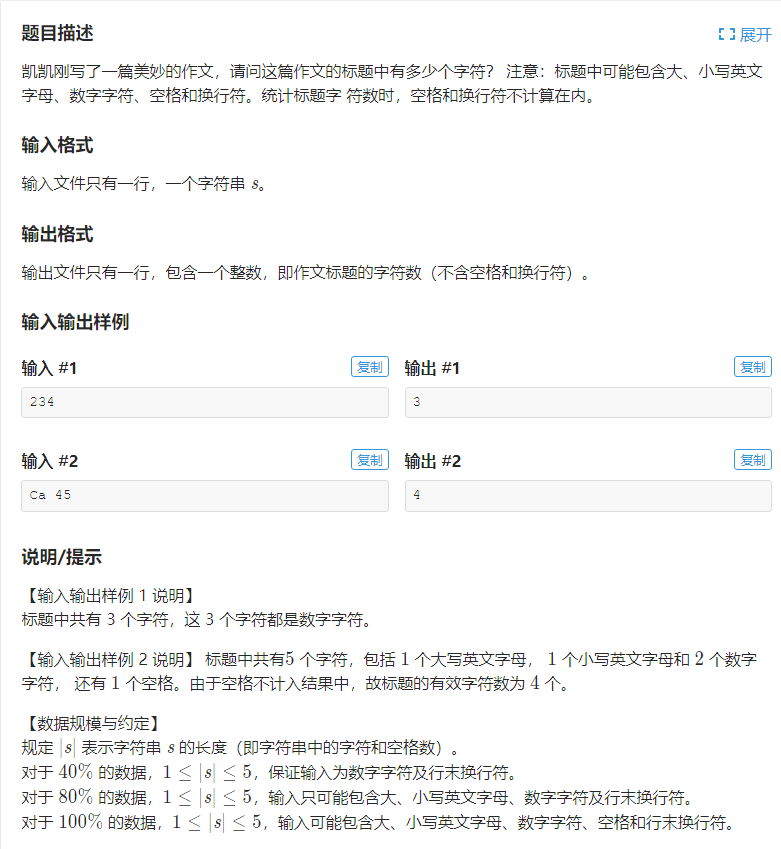
首先简化一下题目——给定一个仅含大 小写字母，数字，与空格的长度不超过5的字符串，求去掉空格后还有几个字符

Noip惯例，第一题依旧是签到题，但是考了字符串，要是不懂关于字符串的输入输出那就要吃大亏了，我在这里使用while+getchar()的方法输入。

直接贴代码——

#include<iostream>
#include<cstdio>
using namespace std;
int ans;
char a;
int main()
{
    while((a=getchar())!='\n')
    {
        if(a!=' ')
        {
            ans++;
        }
    }
    printf("%d",ans);
 } 

标题统计

---

T2：龙虎斗

题面：

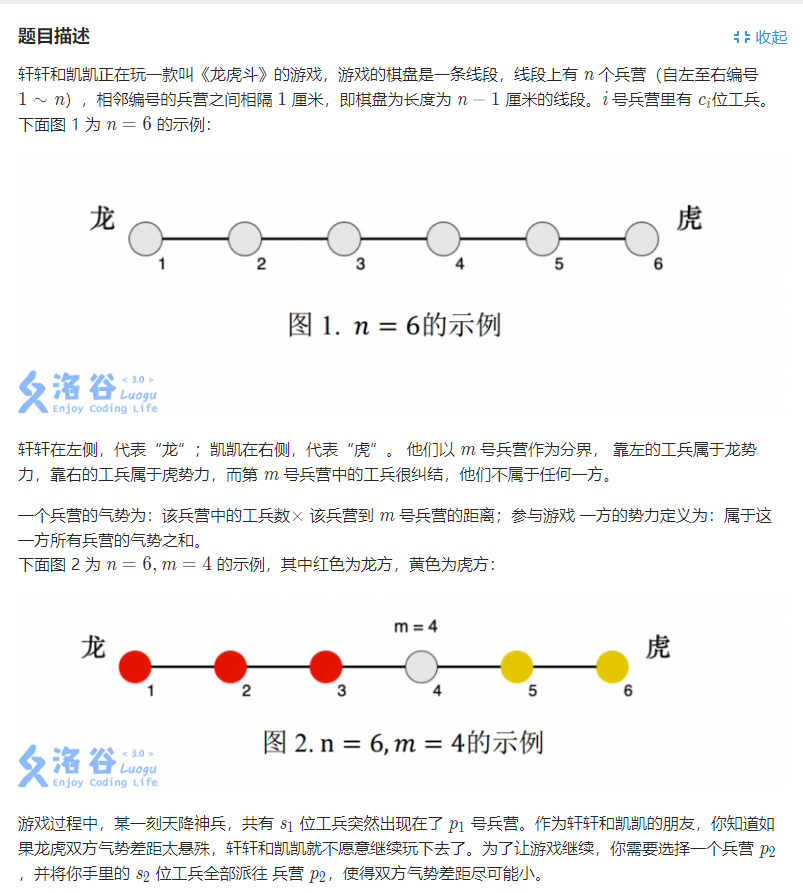
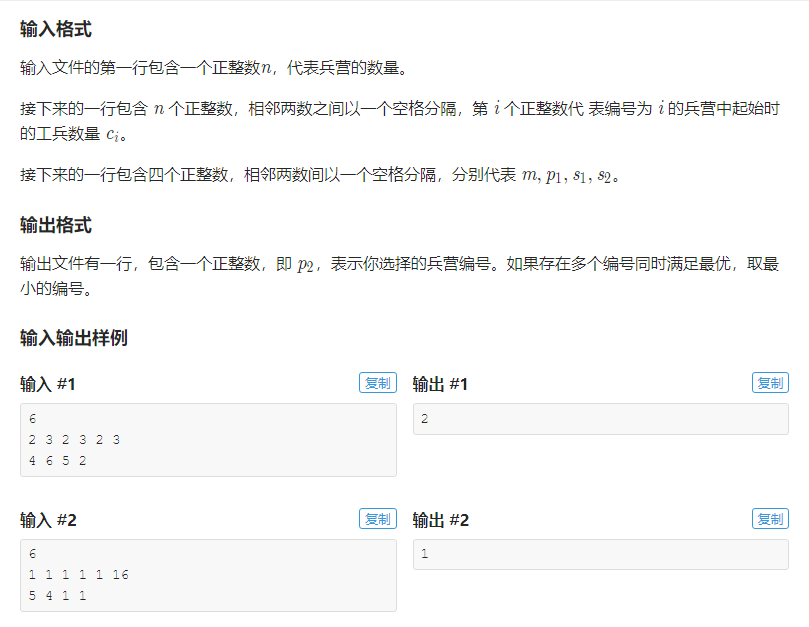
简化题目：有n个点，带点权，其中有一个点（称为m点），在m点左边的点集合称为龙队,在m点右边的点集合称为虎队，一个点对于集合的贡献是这个点到m点的距离乘上它的点权。我们会指定一个点增加一定的点权，你可以在这n个点中选择一个点来对它的点权增加一定值，使二个集合中的点对于集合的贡献之和差最小。

只需要先处理两个集合的值，再枚举确定答案就好。这道题要注意事项挺多的：首先对于最小值的初始值要定为long long的最大值，然后要再枚举时分别处理m点左边，m点本身，m点右边对于差值的影响。

只要注意好这些就可以A了这道题了wow（考试的时候因为没有处理左边和右边的差别一直调不出来，以为有锅，转战T3，你们应该懂的）

贴代码（码风难看）：

#include<iostream>
#include<cstdio>
#include<cmath>
#include<climits>//使用 LLONG_MAX所需要的头文件
using namespace std;
long long a[1000000],Long,Hu,p1,m,s1,s2,n,minn=LLONG_MAX,minm,p2;
long long dui(long long a)
{
    if(a>=0)
    return a;
    else
    return -1*a;
}
int main()
{
    scanf("%lld",&n);
    for(long long i=1;i<=n;i++)
    {
        scanf("%lld",&a[i]);
    }
    scanf("%lld%lld%lld%lld",&m,&p1,&s1,&s2);
    a[p1]+=s1;
    for(long long i=1;i<=m-1;i++)
    {
        Long+=a[i]*(m-i);
    }
    for(long long i=m+1;i<=n;i++)
    {
        Hu+=a[i]*(i-m);
    }
    for(long long i=1;i<=n;i++)
    {
       minm=minn;
       if(i<=m)
       {
                   minn=min(minn,dui(Long+s2*(m-i)-Hu));
       }
       else
       minn=min(minn,dui(Long-(Hu+s2*(i-m))));
       if(minn!=minm)
       {
           p2=i;
       }
    }
    printf("%lld",p2);
    return 0;
}

龙虎斗

---

T4：对称二叉树（为什么先说T4，因为T3比T4难啊）

题面：

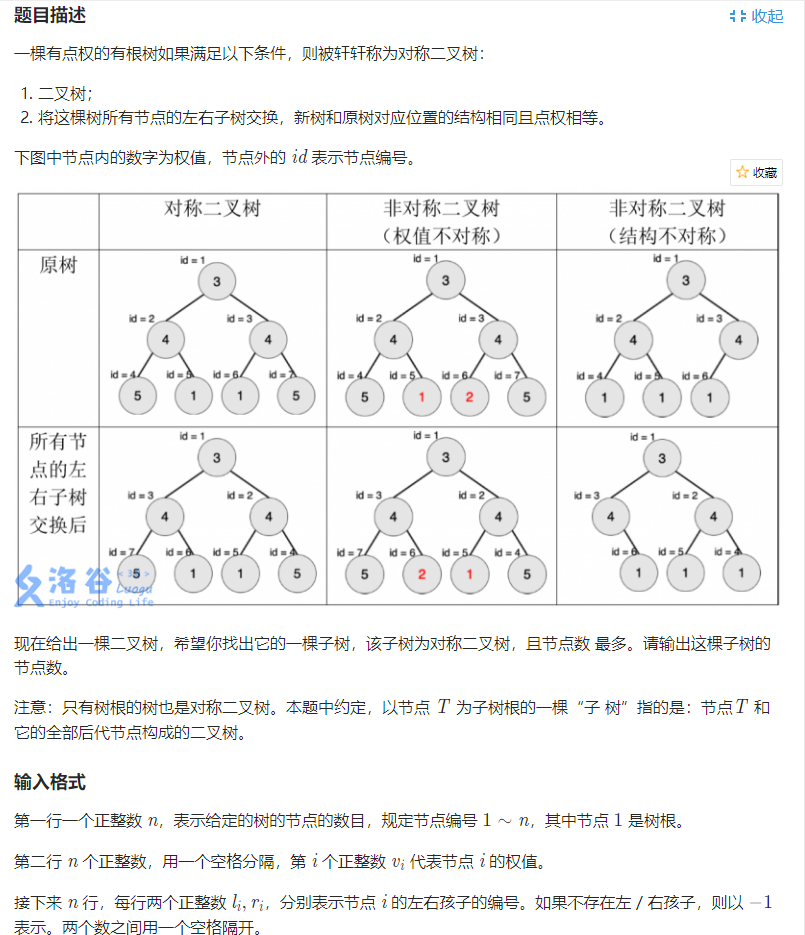
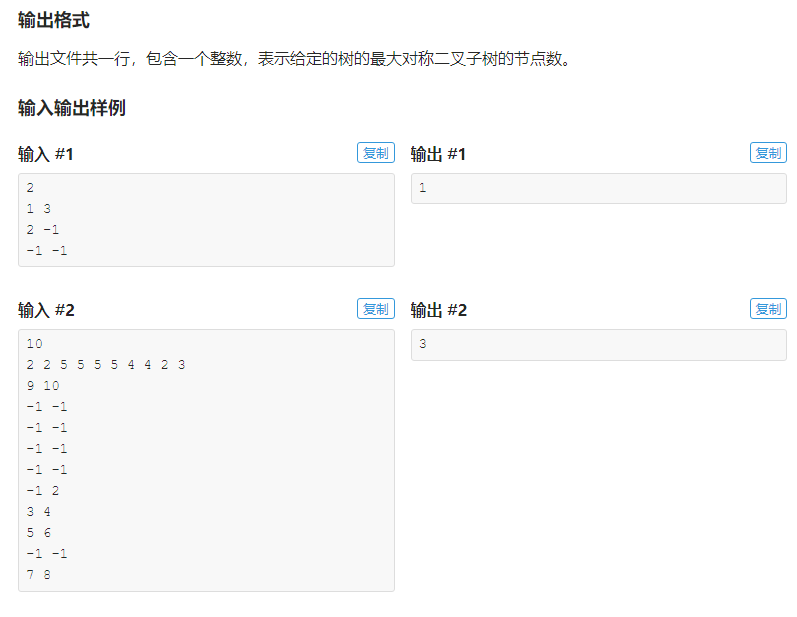
就不简化了吧，题目讲得很清楚

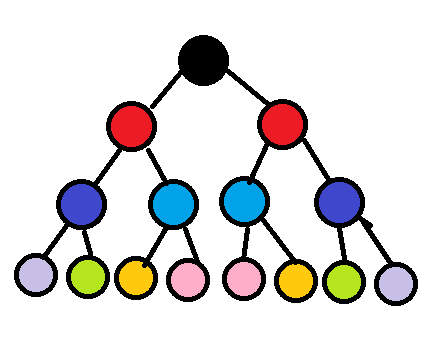
我们看到这个以黑色为根的对称二叉树，我已经给它染上色了，我们可以发现其实每一层以颜色来看就一个回文串。

所以其实我们可以这样定义一颗对称二叉树：1：满足是一颗满二叉树 2：对于每一层的结点的权值连起来可以组成回文串

我们现在再想一下——怎么判断这一层的节点是回文串，其实这是一个极易发现的性质对于这一层的上一层（假设上一层也是一个回文串）来说上一层回文串中的一个父亲的左儿子等于与这个父亲节点相对应的父亲节点的右儿子，反过来左儿子也会等于右儿子，假如对于上一层的所有点对都满足这个性质，那么这一层就是一个回文串（可以自己手画几张图）

这是一个可以递归的过程！

只要我们枚举每个点为根，再进行上述的递归，就可以知道以这个点为根的子树是否是对称二叉树，假如是对称二叉树，它的子树大小（在递归时统计一下就好了）

可以贴代码啦：

#include<iostream>
#include<cstdio>
#include<algorithm>
using namespace std;
struct tree{
    long long data;
    long long left_child;
    long long right_child;
    long long size;
}a[1000009];
bool p;
long long cheek(long long left,long long right,long long sum)
{
    if(left==-1&&right==-1)
    return 0;
    if(left==-1||right==-1)
    {
      p=0;
      return 0;
    }
    if(a[left].data!=a[right].data)
    {
        p=0;
        return 0;
    }
    return cheek(a[left].left_child,a[right].right_child,1)+cheek(a[left].right_child,a[right].left_child,1)+sum;
}
long long n,left,right,maxn=1;
int main()
{
   scanf("%lld",&n);
   for(long long i=1;i<=n;i++)
   {
       scanf("%lld",&a[i].data);
   }
   for(long long i=1;i<=n;i++)
   {
           scanf("%lld%lld",&a[i].left_child,&a[i].right_child);
   }
   for(long long i=1;i<=n;i++)
   {
    p=1;
    long long now=cheek(i,i,1);
       if(p)
       maxn=max(maxn,now);
   }
   printf("%lld",maxn);
} 

对称二叉树

---

T3：摆渡车(DP）

题目就不摆了吧 这道题应该广为流传 Noip近几年最难的题目

但是其实说实话难是难在拿满分，但其实可以轻松拿到70分（开O2是可以满分的）

我们不妨认为时间是一条数轴，每名同学按照到达时刻分别对应数轴上可能重合的点。安排车辆的工作，等同于将数轴分成若干个左开右闭段，每段的长度⩾m。原本的等车时间之和，自然就转换成所有点到各自所属段右边界的距离之和。

可以结合下面这副图思考

其实我们只需要枚举每一段的右边界i和这一段的上一个右边界j就好了

那么关于这个 j-i区间的值

就是这个区间里的数的数量*i减去在这个区间的每个数的值的和

这样我们便可以求出从1到i中等待值最小做法

依靠这个，我们便有了五十分的做法（纯模拟）

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cmath>
using namespace std;
const int MAXN=4000005;
long long f[MAXN],n,m,T[MAXN],cou[MAXN],t,t1;
long long ans=0xef1000000;
int main()
{
    scanf("%lld%lld",&n,&m);
    for(long long i=1;i<=n;i++)
    {
        scanf("%lld",&t1);
        cou[t1]++;
        T[t1]+=t1;
        t=std::max(t,t1);
    }
    for(long long i=1;i<t+m;i++)
    {
        cou[i]+=cou[i-1];
        T[i]+=T[i-1];
    }
    for(long long i=0;i<t+m;i++)
    {
        f[i]=cou[i]*i-T[i];
        for(long long j=std::max(i-m-m+1,(long long)0);j<=i-m;j++)
        {
            f[i]=std::min(f[j]+(cou[i]-cou[j])*i-(T[i]-T[j]),f[i]);
        }
    }
    for(long long i=t;i<t+m;i++)
    {
        ans=std::min(ans,f[i]);
    }
    printf("%lld",ans);
}

摆渡车（50分纯模拟）

但我们这个纯模拟的DP还有优化的空间，我们其实很容易想到我们枚举j完全不需要从1开始，我们可以从i-2*m开始，因为在i-2*m以前，完全可以先开走一趟，明显不会影响后面的答案。所以我们可以通过上下界优化来达到70分（这个版本O2优化可以满分）

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cmath>
using namespace std;
const int MAXN=4000005;
long long f[MAXN],n,m,T[MAXN],cou[MAXN],t,t1;
long long ans=0xef1000000;
int main()
{
    scanf("%lld%lld",&n,&m);
    for(long long i=1;i<=n;i++)
    {
        scanf("%lld",&t1);
        cou[t1]++;
        T[t1]+=t1;
        t=std::max(t,t1);
    }
    for(long long i=1;i<t+m;i++)
    {
        cou[i]+=cou[i-1];
        T[i]+=T[i-1];
    }
    for(long long i=0;i<t+m;i++)
    {
        f[i]=cou[i]*i-T[i];
        for(long long j=std::max(i-m-m+1,(long long)0);j<=i-m;j++)
        {
            f[i]=std::min(f[j]+(cou[i]-cou[j])*i-(T[i]-T[j]),f[i]);
        }
    }
    for(long long i=t;i<t+m;i++)
    {
        ans=std::min(ans,f[i]);
    }
    printf("%lld",ans);
}

摆渡车（如果带O2优化满分 上下界优化）

（目前博主的实力只能写出这个版本，如果想达到满分需要使用斜率优化，然鹅博主还是一个初三的学生，很多东西学得很慢，所以斜率优化正在学，学会了之后会回来补上满分版本这个坑吧QWQ）

（好了，本篇题解就到这里了，慢走）

（有什么不懂可以加qq2733524923我们一起探讨哦）QWQ