[CSP-S2021] 括号序列

链接：

P7914

---

题意：

有一堆规则，然后判断给定字符串有多少种填法符合规则。

---

分析：

一眼区间dp，状态数 \(n^2\)，我们来分析这些规则。

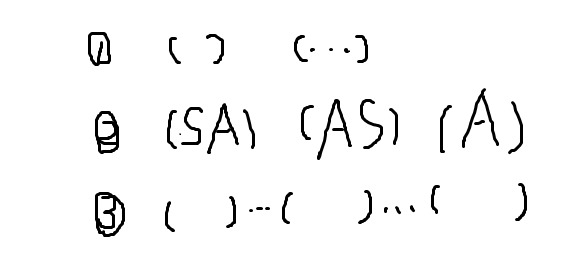
把这些规则分成三类，第一类可以预处理出区间是否能表达成全部都是 * 的情况并且其长度小于等于 \(k\)，后 \(O(1)\) 判断。第二类可以考虑枚举 \(S\) 的长度，\(O(n)\) 处理。第三类如果枚举分割点显然会算重，依套路我们枚举第一个括号的位置且要保证第一个括号无法被继续分割，考虑在每个区间维护一个无法被分割的方案数，也就是不计第三类的方案，记做 \(dp[l][r][0]\)，总方案数记做 \(dp[l][r][1]\)，然后再枚举点的长度，\(O(n^2)\) 处理，时间复杂度 \(O(n^4)\)。

---

优化：

对于第三类的处理，假如我们固定第一个括号的位置，那么需要被计算的其实是一个后缀和。这里我固定除去第一个括号的后面括号的位置，那么就是一个前缀和，两者没有什么区别。大概长这样：

于是我们考虑做一个前缀和，就是 \(sum[l][r]=\sum\limits_{k=l}^r dp[l][i][0]\)

那么第三类的转移只需要处理出前缀和左边的边界就可以 \(O(n)\) 转移了，这个边界会受到三个限制，一是至少要大于等于 \(l\)，其次与 \(r\) 的距离会受到 \(k\) 的限制，再是如果前面有一个位置不能表示为 *，显然从这之前的都不能算，所以只需要预处理出一个位置之前最近的不能表示为 * 的位置就好了。然后还有一个细节就是这样做会多减一个没有 * 的情况，加上就好了。

时间复杂度 \(O(n^3)\)

---

算法：

先预处理出区间是否能表达成全部都是 * 的情况并且其长度小于等于 \(k\)，以及一个位置之前最近的不能表示为 * 的位置，然后根据规则 dp 同时维护前缀和就好了。

---

代码：

#include<bits/stdc++.h>
using namespace std;
#define int long long
#define in read()
inline int read(){
	int p=0,f=1;
	char c=getchar();
	while(!isdigit(c)){if(c=='-')f=-1;c=getchar();}
	while(isdigit(c)){p=p*10+c-'0';c=getchar();}
	return p*f;
}
const int N=505;
const int mod=1e9+7;
int n,k,sum[N],dp[N][N][2],h[N][N],ex[N][N],last[N];
char s[N];
inline int add(int x,int y){int z=x+y;return (z>=mod)?(z-mod):z;}
inline int mul(int x,int y){int z=x*y;return (z>=mod)?(z%mod):z;}
inline void Add(int &x,int y){x=add(x,y);}
inline void Mul(int &x,int y){x=mul(x,y);}
signed main(){
	freopen("bracket.in","r",stdin);
	freopen("bracket.out","w",stdout);
	cin>>n>>k>>(s+1);
	for(int i=1;i<=n;i++)
		if(s[i]=='*'||s[i]=='?')
			sum[i]=sum[i-1]+1,last[i]=last[i-1];
		else
			last[i]=i,sum[i]=sum[i-1];
	for(int i=1;i<=n;i++)
		for(int j=1;j<=n;j++)
			if((sum[j]-sum[i-1]==j-i+1&&j-i+1<=k)||j<i)
				h[i][j]=1;
			else h[i][j]=0;
	for(int i=1;i<n;i++)
		if((s[i]=='('||s[i]=='?')&&(s[i+1]==')'||s[i+1]=='?'))
			dp[i][i+1][0]=dp[i][i+1][1]=ex[i][i+1]=1;
	for(int i=3;i<=n;i++)
		for(int l=1,r=l+i-1,temp=min(r-l-3,k);r<=n;l++,r=l+i-1){
			if((s[l]=='('||s[l]=='?')&&(s[r]==')'||s[r]=='?')){
				if(h[l+1][r-1])dp[l][r][0]++;
				if(l+1<r-1)Add(dp[l][r][0],dp[l+1][r-1][1]);//1
				if(s[l+1]=='('||s[l+1]=='?')
					for(int t=1;t<=temp;t++)
						Add(dp[l][r][0],dp[l+1][r-1-t][1]*h[r-t][r-1]);
				if(s[r-1]==')'||s[r-1]=='?')
					for(int t=1;t<=temp;t++)
						Add(dp[l][r][0],dp[l+1+t][r-1][1]*h[l+1][l+t]);//2
				dp[l][r][1]=dp[l][r][0];
				for(int t=r-1;t>=l+2;t--){
					int ll=max(t-1-k,l);
					ll=max(ll,last[t-1]);
					Add(dp[l][r][1],mul(dp[t][r][1],add(add(ex[l][t-1]-ex[l][ll],dp[l][ll][0]),mod)));
				}//3
			}
			ex[l][r]=add(ex[l][r-1],dp[l][r][0]);//前缀和
		}
	cout<<dp[1][n][1];
	return 0;
}

题外话：

区间dp做少了。