python中一些算法数列

斐波那契数列：

 1 def fn(n):
 2     if n==1:
 3         return 1
 4     elif n==2:
 5         return 1
 6     else:
 7         return fn(n-1)+fn(n-2)
 8
 9 for i in range(1,10):
10     print(fn(i))

 python实现输出黑白棋盘：

 for i in range(1,11):
     for j in range(1,11):
         if (i+j)%2==0:
             print('■',end='')
         else:
             print('□', end='')
     print('\n')

输出由1,2,3,4 这四个数字组成的每位数都不相同的 所有三位数

 list1 = [1,2,3,4]

 for i in list1:
     for k in list1:
         for j in list1:
             if i != k and k != j and i != j:
                 print(i*100+k*10+j)

 python 实现冒泡排序

 import random

 def bubbleSort(lis):
     length = len(lis)
     for i in range(0,length):        #下标为0，1，2，3，4，5
         for j in range(i+1,length):  #下标为1，2，3，4，5，6
             if lis[i] > lis[j]:　　　 #相邻的两位数进行比较
                 lis[j],lis[i] = lis[i],lis[j]      #进行数据交换

 lis = [random.randint(1,100) for i in range(20)]  #随机生成长度为20的 列表
 bubbleSort(lis)

 python 实现二分法查找

l = [2,3,5,10,15,16,18,22,26,30,32,35,41,42,43,55,56,66,67,69,72,76,82,83,88]

你观察这个列表，这是不是一个从小到大排序的 有序 列表呀？

如果这样，假如我要找的数比列表中间的数还大，是不是我直接在列表的后半边找就行了？

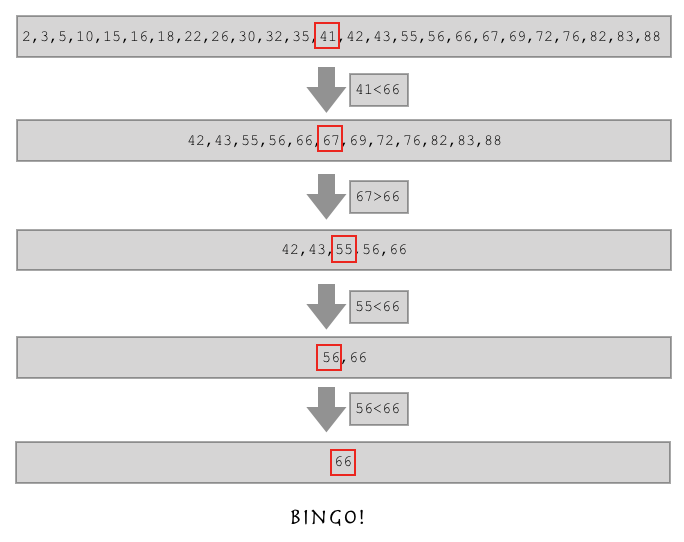
l = [2,3,5,10,15,16,18,22,26,30,32,35,41,42,43,55,56,66,67,69,72,76,82,83,88]
def find2(l, num, start=0, end=None):
    end = end if end else len(l) - 1        #程序执行开始先找列表中间值的下标
    mid = (end-start)//2 + start　　　　　　  #计算列表中间值得下标
    if start > end:　　　　　　　　　　　　　　 #如果满足这个条件，则说明查找一遍无法找到匹配的结果
        print('找不到')
    elif l[mid] > num:　　　　　　　　　　　　　#如果被查找的数没有中间的数字大，则递归调用自身从列表的左边开始比较，注意end的值
        find2(l, num, end=mid)　　　　
    elif l[mid] < num:　　　　　　　　　　　　　#如果被查找的数比中间的数字大，则递归调用自身从列表的右边开始查找，开始位置是中间值下标+1，末尾下标还是末尾的下标
        find2(l, num, start=mid+1, end=end)
    else:　　　　　　　　　　　　　　　　　　　　　#条件都不符合  则说明已找到 该值得下标　　
        print('找到啦', mid)

find2(l,88)   #比如找88的下标

请证明 一个偶数是两个素数的和

def su(n):
    for i in range(2,n//2+1):
        if n%i == 0:
            return False
    else:
        return True

if __name__ == '__main__':
    while True:
        n =int(input('please input a num'))
        if n%2 == 0:
            break

    for i in range(2,n//2+1):
        if su(i) and su(n-i):
            print(i,'+',n-i,'=',n)