算法问题实战策略 BOARDCOVER

地址 https://algospot.com/judge/problem/read/BOARDCOVER

解法

DFS 最近似乎在简单DFS上花费太多时间了

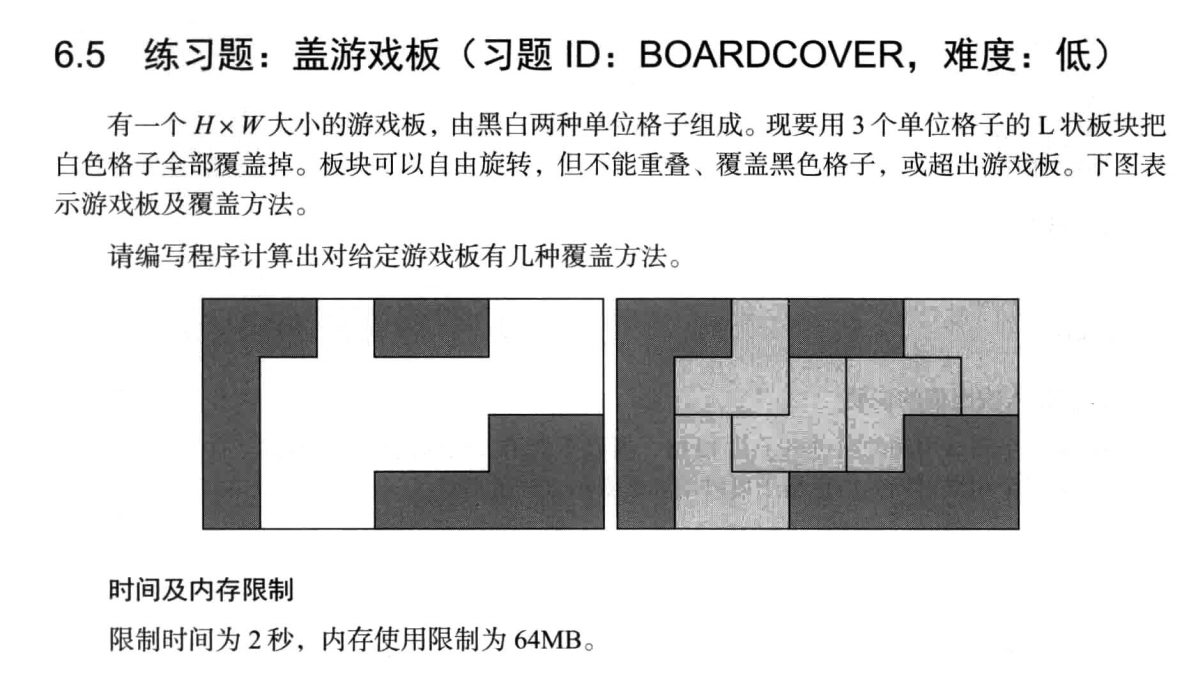
首先扫描地图 统计可覆盖的元素个数 如果不是3的倍数 那肯定不能覆盖完全 返回0

然后进行DFS 尝试各种覆盖办法 一共12种(由于必须覆盖完所有元素 就规定从左上角开始覆盖，其实可以只有四种覆盖办法)

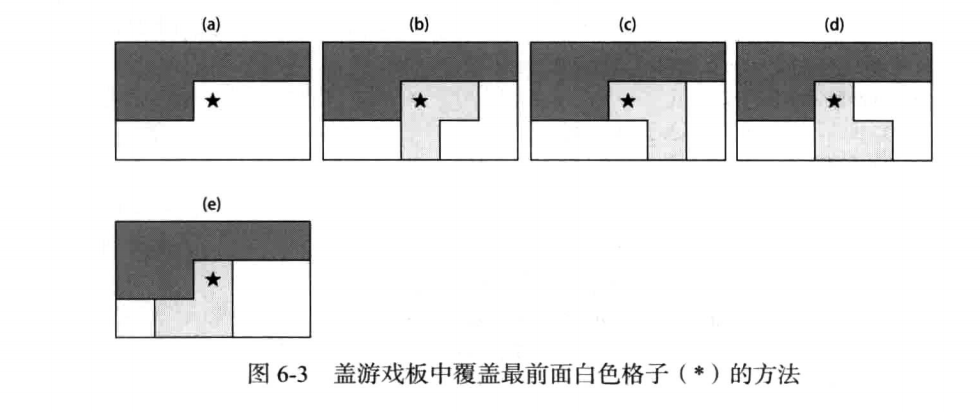
每次DFS结束则覆盖方法增加1种  尝试所有覆盖方式后 函数也返回

注意需要寻找每次下一个尝试的覆盖点 规定从左上角开始找起

代码

// 11111111111111.cpp : 此文件包含 "main" 函数。程序执行将在此处开始并结束。
//

#include <iostream>
#include <vector>

using namespace std;

const int N = ;

char gmap[N][N];

int loop;
int ans = ;
int n, m;

struct board {
    int x1, y1;
    int x2, y2;
    int x3, y3;
};

vector<struct board> fillBoad=
{
    {,, -,, ,-},
    {,, ,,  ,-},
    {,, -,, ,},
    {,, ,,  ,},

    {,, ,,  ,-},
    {,, -,, -,-},
    {,, ,,  ,},
    {,, -,, -,},

    {,, ,,  -,},
    {,, ,,  ,},
    {,, ,-, ,-},
    {,, ,-, --},
};

bool CheckXY(int x1, int y1, int x2, int y2, int x3, int y3)
{
    if (x1 <  || y1 <  || x2 <  || y2 <  || x3 <  || y3 < )
        return false;

    if (x1 >= n || x2 >= n || x3 >= n || y1 >= m || y2 >= m || y3 >= m)
        return false;

    if (gmap[x1][y1] == '#' || gmap[x2][y2] == '#' || gmap[x3][y3] == '#')
        return false;

    return true;
}

void DFS(int x, int y,int needfill)
{
    if (needfill == ) {
        ans++;
        return;
    }

    for (; x < n; x++) {
        for ( y = ; y < m; y++) {
            if (gmap[x][y] == '.')
                goto FIND;
        }
    }
    FIND:

    for (int i = ; i < ; i++) {

        int newx1 = x + fillBoad[i].x1;
        int newy1 = y + fillBoad[i].y1;
        int newx2 = x + fillBoad[i].x2;
        int newy2 = y + fillBoad[i].y2;
        int newx3 = x + fillBoad[i].x3;
        int newy3 = y + fillBoad[i].y3;

        if (CheckXY(newx1, newy1, newx2, newy2, newx3,newy3)) {
            gmap[newx1][newy1] = '#';
            gmap[newx2][newy2] = '#';
            gmap[newx3][newy3] = '#';
            needfill -= ; 

            int p = x; int q = y;
            for (; p < n; p++) {
                for ( q = ; q < m; q++) {
                    if (gmap[p][q] == '.')
                        goto FIND1;
                }
            }

            FIND1:

            DFS( p,q, needfill);

            needfill += ;
            gmap[newx1][newy1] = '.';
            gmap[newx2][newy2] = '.';
            gmap[newx3][newy3] = '.';

        }
    }

    return;
}

int main()
{
    cin >> loop;

    while (loop--)
    {
        cin >> n >> m;

        memset(gmap,,N*N);
        ans = ;

        int count = ;
        for (int i = ; i < n; i++) {
            for (int j = ; j < m; j++) {
                cin >> gmap[i][j];
                if (gmap[i][j] == '.')
                    count++;
            }
        }

        if (count %  != ){
            cout <<  << endl;
            continue;
        }

        DFS(,,count);
        cout << ans << endl;
    }

    return ;
}

ac