通俗地说决策树算法（三）sklearn决策树实战

前情提要

通俗地说决策树算法（一）基础概念介绍

通俗地说决策树算法（二）实例解析

上面两篇介绍了那么多决策树的知识，现在也是时候来实践一下了。Python有一个著名的机器学习框架，叫sklearn。我们可以用sklearn来运行前面说到的赖床的例子。不过在这之前，我们需要介绍一下sklearn中训练一颗决策树的具体参数。

另外sklearn中训练决策树的默认算法是CART，使用CART决策树的好处是可以用它来进行回归和分类处理，不过这里我们只进行分类处理。

一. sklearn决策树参数详解

我们都知道，一个模型中很重要的一步是调参。在sklearn中，模型的参数是通过方法参数来决定的，以下给出sklearn中，决策树的参数：

DecisionTreeClassifier(criterion="gini",
                 splitter="best",
                 max_depth=None,
                 min_samples_split=2,
                 min_samples_leaf=1,
                 min_weight_fraction_leaf=0.,
                 max_features=None,
                 random_state=None,
                 max_leaf_nodes=None,
                 min_impurity_decrease=0.,
                 min_impurity_split=None,
                 class_weight=None,
                 presort=False)

参数含义：
1.criterion:string, optional (default="gini")
            (1).criterion='gini',分裂节点时评价准则是Gini指数。
            (2).criterion='entropy',分裂节点时的评价指标是信息增益。
2.max_depth:int or None, optional (default=None)。指定树的最大深度。
            如果为None，表示树的深度不限。直到所有的叶子节点都是纯净的，即叶子节点
            中所有的样本点都属于同一个类别。或者每个叶子节点包含的样本数小于min_samples_split。
3.splitter:string, optional (default="best")。指定分裂节点时的策略。
           (1).splitter='best',表示选择最优的分裂策略。
           (2).splitter='random',表示选择最好的随机切分策略。
4.min_samples_split:int, float, optional (default=2)。表示分裂一个内部节点需要的做少样本数。
           (1).如果为整数，则min_samples_split就是最少样本数。
           (2).如果为浮点数(0到1之间)，则每次分裂最少样本数为ceil(min_samples_split * n_samples)
5.min_samples_leaf: int, float, optional (default=1)。指定每个叶子节点需要的最少样本数。
           (1).如果为整数，则min_samples_split就是最少样本数。
           (2).如果为浮点数(0到1之间)，则每个叶子节点最少样本数为ceil(min_samples_leaf * n_samples)
6.min_weight_fraction_leaf:float, optional (default=0.)
           指定叶子节点中样本的最小权重。
7.max_features:int, float, string or None, optional (default=None).
           搜寻最佳划分的时候考虑的特征数量。
           (1).如果为整数，每次分裂只考虑max_features个特征。
           (2).如果为浮点数(0到1之间)，每次切分只考虑int(max_features * n_features)个特征。
           (3).如果为'auto'或者'sqrt',则每次切分只考虑sqrt(n_features)个特征
           (4).如果为'log2',则每次切分只考虑log2(n_features)个特征。
           (5).如果为None,则每次切分考虑n_features个特征。
           (6).如果已经考虑了max_features个特征，但还是没有找到一个有效的切分，那么还会继续寻找
           下一个特征，直到找到一个有效的切分为止。
8.random_state:int, RandomState instance or None, optional (default=None)
           (1).如果为整数，则它指定了随机数生成器的种子。
           (2).如果为RandomState实例，则指定了随机数生成器。
           (3).如果为None，则使用默认的随机数生成器。
9.max_leaf_nodes: int or None, optional (default=None)。指定了叶子节点的最大数量。
           (1).如果为None,叶子节点数量不限。
           (2).如果为整数，则max_depth被忽略。
10.min_impurity_decrease:float, optional (default=0.)
         如果节点的分裂导致不纯度的减少(分裂后样本比分裂前更加纯净)大于或等于min_impurity_decrease，则分裂该节点。
         加权不纯度的减少量计算公式为：
         min_impurity_decrease=N_t / N * (impurity - N_t_R / N_t * right_impurity
                            - N_t_L / N_t * left_impurity)
         其中N是样本的总数，N_t是当前节点的样本数，N_t_L是分裂后左子节点的样本数，
         N_t_R是分裂后右子节点的样本数。impurity指当前节点的基尼指数，right_impurity指
         分裂后右子节点的基尼指数。left_impurity指分裂后左子节点的基尼指数。
11.min_impurity_split:float
         树生长过程中早停止的阈值。如果当前节点的不纯度高于阈值，节点将分裂，否则它是叶子节点。
         这个参数已经被弃用。用min_impurity_decrease代替了min_impurity_split。
12.class_weight:dict, list of dicts, "balanced" or None, default=None
         类别权重的形式为{class_label: weight}
         (1).如果没有给出每个类别的权重，则每个类别的权重都为1。
         (2).如果class_weight='balanced'，则分类的权重与样本中每个类别出现的频率成反比。
         计算公式为：n_samples / (n_classes * np.bincount(y))
         (3).如果sample_weight提供了样本权重(由fit方法提供)，则这些权重都会乘以sample_weight。
13.presort:bool, optional (default=False)
        指定是否需要提前排序数据从而加速训练中寻找最优切分的过程。设置为True时，对于大数据集
        会减慢总体的训练过程；但是对于一个小数据集或者设定了最大深度的情况下，会加速训练过程。

虽然看起来参数众多，但通常参数都会有默认值，我们只需要调整其中较为重要的几个参数就行。

通常来说，较为重要的参数有：

1. criterion：用以设置用信息熵还是基尼系数计算。
2. splitter：指定分支模式
3. max_depth：最大深度，防止过拟合
4. min_samples_leaf：限定每个节点分枝后子节点至少有多少个数据，否则就不分枝

二. sklearn决策树实战

2.1 准备数据及读取

数据就是上次说到的赖床特征，

季节	时间已过 8 点	风力情况	要不要赖床
spring	no	breeze	yes
winter	no	no wind	yes
autumn	yes	breeze	yes
winter	no	no wind	yes
summer	no	breeze	yes
winter	yes	breeze	yes
winter	no	gale	yes
winter	no	no wind	yes
spring	yes	no wind	no
summer	yes	gale	no
summer	no	gale	no
autumn	yes	breeze	no

将它存储成 csv 文件

spring,no,breeze,yes
winter,no,no wind,yes
autumn,yes,breeze,yes
winter,no,no wind,yes
summer,no,breeze,yes
winter,yes,breeze,yes
winter,no,gale,yes
winter,no,no wind,yes
spring,yes,no wind,no
summer,yes,gale,no
summer,no,gale,no
autumn,yes,breeze,no

2.2 决策树的特征向量化DictVectorizer

sklearn的DictVectorizer能对字典进行向量化。什么叫向量化呢？比如说你有季节这个属性有[春,夏,秋,冬]四个可选值，那么如果是春季，就可以用[1,0,0,0]表示，夏季就可以用[0,1,0,0]表示。不过在调用DictVectorizer它会将这些属性打乱，不会按照我们的思路来运行，但我们也可以一个方法查看，我们看看代码就明白了。

import pandas as pd
from sklearn.feature_extraction import DictVectorizer
from sklearn import tree
from sklearn.model_selection import train_test_split

#pandas 读取 csv 文件，header = None 表示不将首行作为列
data = pd.read_csv('data/laic.csv',header =None)
#指定列
data.columns = ['season','after 8','wind','lay bed']

#sparse=False意思是不产生稀疏矩阵
vec=DictVectorizer(sparse=False)
#先用 pandas 对每行生成字典，然后进行向量化
feature = data[['season','after 8','wind']]
X_train = vec.fit_transform(feature.to_dict(orient='record'))
#打印各个变量
print('show feature\n',feature)
print('show vector\n',X_train)
print('show vector name\n',vec.get_feature_names())

我们来看看打印的结果：

show feature
     season after 8     wind
0   spring      no   breeze
1   winter      no  no wind
2   autumn     yes   breeze
3   winter      no  no wind
4   summer      no   breeze
5   winter     yes   breeze
6   winter      no     gale
7   winter      no  no wind
8   spring     yes  no wind
9   summer     yes     gale
10  summer      no     gale
11  autumn     yes   breeze
show vector
 [[1. 0. 0. 1. 0. 0. 1. 0. 0.]
 [1. 0. 0. 0. 0. 1. 0. 0. 1.]
 [0. 1. 1. 0. 0. 0. 1. 0. 0.]
 [1. 0. 0. 0. 0. 1. 0. 0. 1.]
 [1. 0. 0. 0. 1. 0. 1. 0. 0.]
 [0. 1. 0. 0. 0. 1. 1. 0. 0.]
 [1. 0. 0. 0. 0. 1. 0. 1. 0.]
 [1. 0. 0. 0. 0. 1. 0. 0. 1.]
 [0. 1. 0. 1. 0. 0. 0. 0. 1.]
 [0. 1. 0. 0. 1. 0. 0. 1. 0.]
 [1. 0. 0. 0. 1. 0. 0. 1. 0.]
 [0. 1. 1. 0. 0. 0. 1. 0. 0.]]
show vector name
 ['after 8=no', 'after 8=yes', 'season=autumn', 'season=spring', 'season=summer', 'season=winter', 'wind=breeze', 'wind=gale', 'wind=no wind']

通过DictVectorizer，我们就能够把字符型的数据，转化成0 1的矩阵，方便后面进行运算。额外说一句，这种转换方式其实就是one-hot编码。

2.4 决策树训练

可以发现在向量化的时候，属性都被打乱了，但我们也可以通过get_feature_names()这个方法查看对应的属性值。有了数据后，就可以来训练一颗决策树了，用sklearn很方便，只需要很少的代码

#划分成训练集，交叉集，验证集，不过这里我们数据量不够大，没必要
#train_x, test_x, train_y, test_y = train_test_split(X_train, Y_train, test_size = 0.3)
#训练决策树
clf = tree.DecisionTreeClassifier(criterion='gini')
clf.fit(X_train,Y_train)

#保存成 dot 文件，后面可以用 dot out.dot -T pdf -o out.pdf 转换成图片
with open("out.dot", 'w') as f :
    f = tree.export_graphviz(clf, out_file = f,
            feature_names = vec.get_feature_names())

2.5 决策树可视化

当完成一棵树的训练的时候，我们也可以让它可视化展示出来，不过sklearn没有提供这种功能，它仅仅能够让训练的模型保存到dot文件中。但我们可以借助其他工具让模型可视化，先看保存到dot的代码：

from sklearn import tree
with open("out.dot", 'w') as f :
    f = tree.export_graphviz(clf, out_file = f,
            feature_names = vec.get_feature_names())

决策树可视化我们用Graphviz这个东西。当然需要先用pip安装对应的库类。然后再去官网下载它的一个发行版本，用以将dot文件转化成pdf图片。

官网下载方式如下：

然后进入到上面保存好的dot所在目录，打开cmd运行dot out.dot -T pdf -o out.pdf 命令，pdf 图片就会出现了。

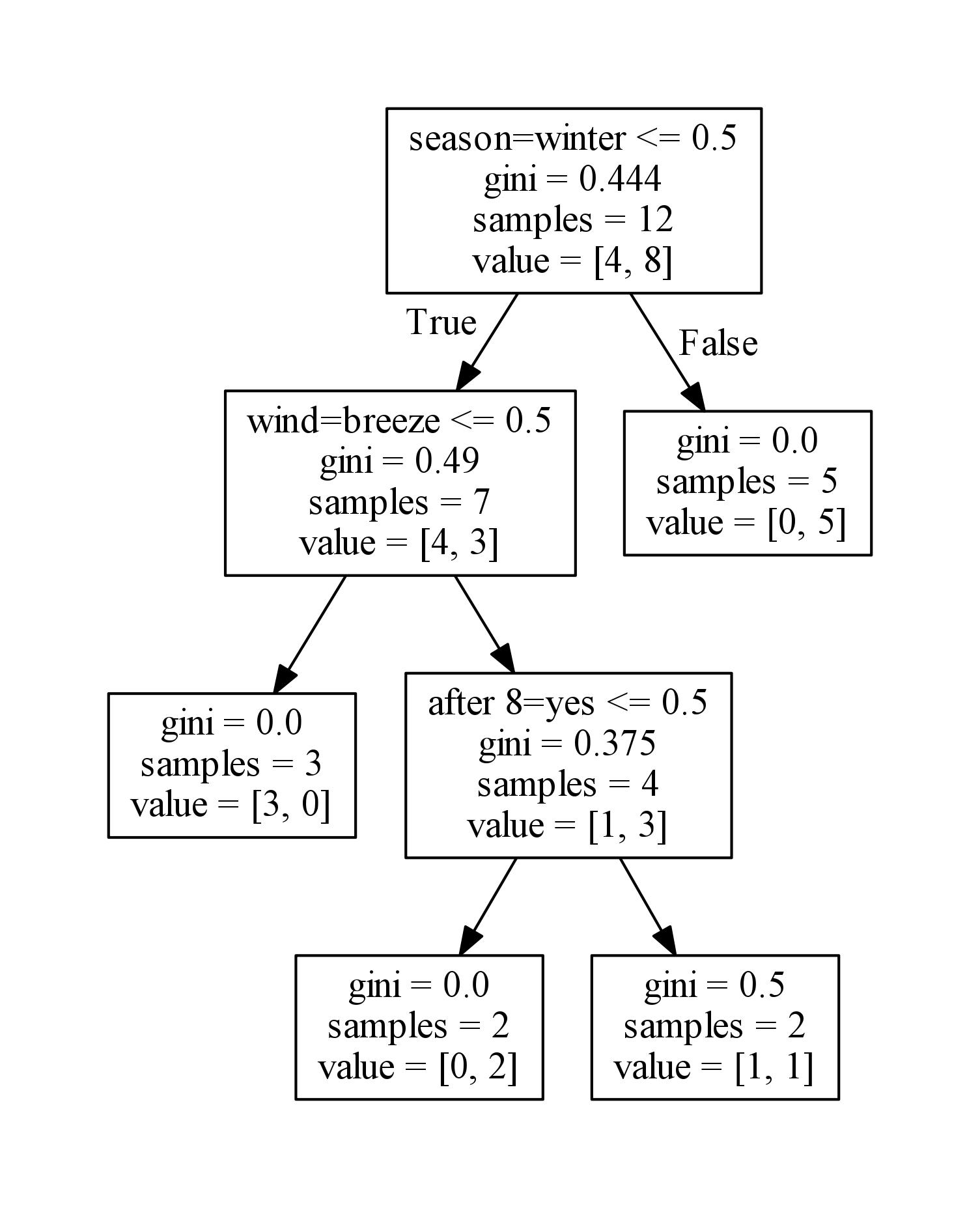
小结：

今天我们介绍了sklearn，决策树模型的各个参数，并且使用sklearn模型对上一节中的例子训练出一个决策树模型，然后用Graphviz让决策树模型可视化。到此，决策树算法算是讲完啦。

以上