Prim算法、Kruskal算法、Dijkstra算法

无向加权图

1.生成树(minimum spanning trees)

图的生成树是它一棵含有所有顶点的无环联通子图

最小生成树:生成树中权值和最小的(所有边的权值之和)

Prim算法、Kruskal算法就是实现最小生成树的算法

• 应用前提:权值各不相同的连通子图(权值相同,最小生成树不唯一)

2.Prim算法

算法描述:

Prim算法是一种"加点法":

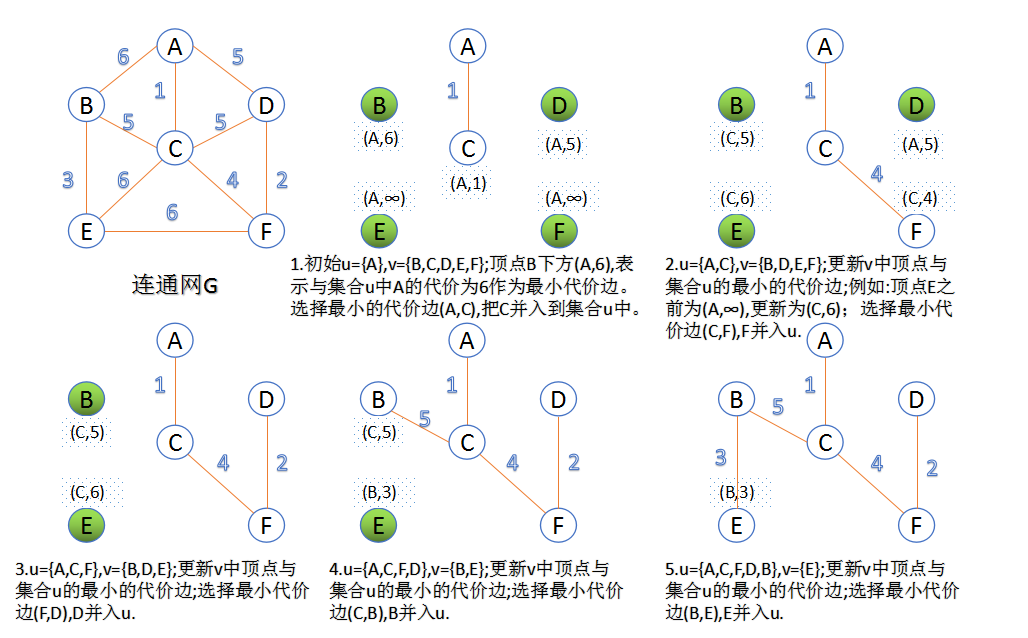
算法步骤:

1.定义图中所有顶点集合\(V\),从顶点\(s\)开始；初始化生成树顶点集合\(u={s}\),\(v=V-u\)

2.遍历结点\({u,v}\)，选择一条权重最小的边，加入到生成树中。\(v\)也进入集合\(u\)中

3.循环步骤2，直至有\(n-1\)条边，或者所有顶点都在最小生成树中。

算法实现

#include<iostream>
#include<vector>
#include<queue>
#include<algorithm>
using namespace std;

#define INFINITE 0xFFFFFFFF
#define VertexData unsigned int     // 图顶点数据类型
#define UNIT unsigned int
#define VertexCounts 6              // 图顶点个数

char vextex[]={'A','B','C','D','E','F'};

struct node                         // prim算法中的边一直更新，最小代价边需要一直更新
{
	VertexData data;
	unsigned int lowestcost;
}closedge[VertexCounts];

typedef struct
{
	VertexData u;
	VertexData v;
	unsigned int cost;

}Arc;                               // 图中结点-边信息

void AdjMatrix(unsigned int adjMat[][VertexCounts])      // 邻接矩阵表示法
{
	for(int i=0;i<VertexCounts;i++)
		for(int j=0;j<VertexCounts;j++)
		{
			adjMat[i][j]=INFINITE;                       // 矩阵元素的初始化
		}
	adjMat[0][1] = 6; adjMat[0][2] = 1; adjMat[0][3] = 5;
    adjMat[1][0] = 6; adjMat[1][2] = 5; adjMat[1][4] = 3;
    adjMat[2][0] = 1; adjMat[2][1] = 5; adjMat[2][3] = 5;
    adjMat[2][4] = 6; adjMat[2][5] = 4;
    adjMat[3][0] = 5; adjMat[3][2] = 5; adjMat[3][5] = 2;
    adjMat[4][1] = 3; adjMat[4][2] = 6; adjMat[4][5] = 6;
    adjMat[5][2] = 4; adjMat[5][3] = 2; adjMat[5][4] = 6;

}

int  Minmum(struct node* closedge)                       // 找到最小代价边
{
	unsigned int min=INFINITE;
	int index=-1;                                        // 保存最小代价边的顶点下标
	for(int i=0;i<VertexCounts;++i)
	{
		if(closedge[i].lowestcost<min && closedge[i].lowestcost!=0)
		{
			min=closedge[i].lowestcost;
			index=i;
		}
	}
	return index;
}

void MiniSpanTree_Prim(unsigned int adjMat[][VertexCounts],VertexData s)
{
	for(i=0;i<VertexCounts;++i)                           // 顶点最小边的初始化
	{
		closedge[i].lowestcost=INFINITE;
	}
	closedge[s].data=s;
	closedge[s].lowestcost=0;
	for(int i=0;i<VertexCounts;++i)
	{
		if(i!=s)
		{
			closedge[i].data=s;
			closedge[i].lowestcost=adjMat[s][i];
		}
	}

	for(int e=1;e<VertexCounts-1;e++)                     // 满足n-1边时候结束循环
	{
		int k=Minmum(closedge);                           // 选择最小代价边
		cout<<vertex[closedge[k].data]<<"--"<<vertex[k]<<endl;

		closedge[k].lowestcost=0;                         // 代价置为0
		for(int i=0;i<VertexCounts;i++)                   // 更新v中的代价信息
		{
			if(adjMat[k][i]<closedge[i].lowestcost)
			{
				closedge[i].data=k;
				closedge[i].lowestcost=adjMat[k][i];
			}
		}
	}
}

int main()
{
    unsigned int  adjMat[vexCounts][vexCounts] = { 0 };
    AdjMatrix(adjMat);                                    //邻接矩阵
    cout << "Prim :" << endl;
    MiniSpanTree_Prim(adjMat,0);                          //Prim算法，从顶点0开始.
    return 0;
}

3.Kruskal算法

算法描述:

Kruskal算法是一种"加边法":

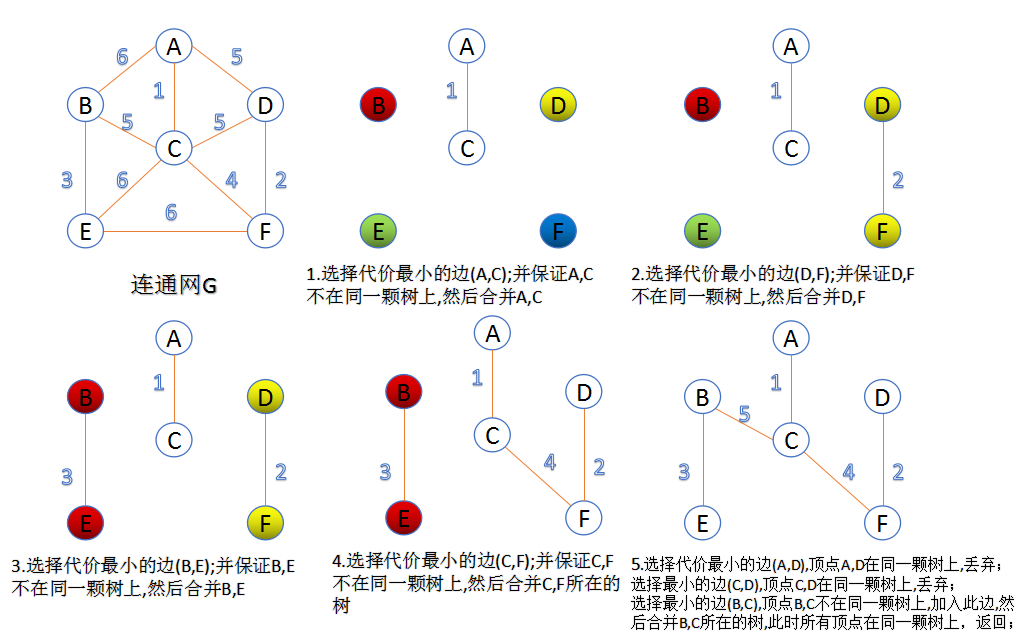
算法步骤:

1.将图中所有的边按权重值进行排序

2.图中n各顶点都是相互独立的

3.权值由小到大选择边，两个顶点应属于两颗不同的树，这样生成最小生成树的一条边。两颗树合并成一颗树。

4.循环步骤3，直至有n-1条边，或者所有顶点都在最小生成树中。

#include<iostream>
#include<vector>
#include<queue>
#include<algorithm>
using namespace std;

#define INFINITE 0xFFFFFFFF
#define VertexData unsigned int     // 图顶点数据类型
#define UNIT unsigned int
#define VertexCounts 6              // 图顶点个数

char vextex[] = { 'A', 'B', 'C', 'D', 'E', 'F' };
typedef struct
{
    VertexData u;
    VertexData v;
    unsigned int cost;              // 边的代价
}Arc;                               // 原始图的边信息

void ReadArc(unsigned int adjMat[][VertexCounts],vector<Arc> &VertexArc) //保存图的边代价信息
{
	Arc* temp=NULL;
	for(unsigned int i=0;i<VertexCounts;i++)
	{
		for(unsigned int j=0;j<VertexCounts;j++)
		{
			if(adjMat[i][j]!=INFINITE)
			{
				temp=new Arc;
				temp->u=i;
				temp->v=j;
				temp->cost=adjMat[i][j];
				VertexArc.push_back(*temp);
			}
		}
	}
}

bool FindTree(VertexData u, VertexData v,vector<vector<VertexData> > &Tree)
{
    unsigned int index_u = INFINITE;
    unsigned int index_v = INFINITE;
    for (unsigned int i = 0; i < Tree.size();i++)  //检查u,v分别属于哪颗树
    {
        if (find(Tree[i].begin(), Tree[i].end(), u) != Tree[i].end())
            index_u = i;
        if (find(Tree[i].begin(), Tree[i].end(), v) != Tree[i].end())
            index_v = i;
    }

    if (index_u != index_v)   //u,v不在一颗树上，合并两颗树
    {
        for (unsigned int i = 0; i < Tree[index_v].size();i++)
        {
            Tree[index_u].push_back(Tree[index_v][i]);
        }
        Tree[index_v].clear();
        return true;
    }
    return false;
}

bool compare(Arc  A, Arc  B)                         // 比较权值的大小
{
    return A.cost < B.cost ? true : false;
}

void MinSpanTree_Kruskal(unsigned int adjMat[][VertexCounts])
{
	vector<Arc> VertexArc;
	ReadArc(adjMat,VertexArc);                       // 读取边信息
	sort(VertexArc.begin(),VertexArc.end(),compare); // 边从小到大排列
	vetor<vector<VertexData>> Tree(VertexCounts);    // 6颗相互独立的树
	for(unsigned int i=0;<VertexCounts;i++)
	{
		Tree[i].push_back(i);                        // 每棵树信息的获取
	}

	for(unsigned int i=0;i<VertexArc.size();i++)
	{
		VertexData u=VertexArc[i].u;
		VertexData v=VertexArc[i].v;

		if(FindTree(u,v,Tree))                        // 检查两个顶点是否在一颗树内
		{
			cout<<vertex[u]<<"--"<<vertex[v]<<endl;
		}
	}
}

int main()
{
    unsigned int  adjMat[vexCounts][vexCounts] = { 0 };
    cout << "-------------" << endl << "Kruskal:" << endl;
    MiniSpanTree_Kruskal(adjMat);//Kruskal算法
    return 0;
}

上面两个算法都是对于无向有权图

在有向加权图中，一般解决最短路径问题

4.Dijkstra算法

算法描述

设G=(V,E)是一个带权有向图，把图中顶点集合V分成两组，第一组为已求出最短路径的顶点集合（用S表示，初始时S中只有一个源点，以后每求得一条最短路径 , 就将加入到集合S中，直到全部顶点都加入到S中，算法就结束了），第二组为其余未确定最短路径的顶点集合（用U表示），按最短路径长度的递增次序依次把第二组的顶点加入S中。在加入的过程中，总保持从源点v到S中各顶点的最短路径长度不大于从源点v到U中任何顶点的最短路径长度。此外，每个顶点对应一个距离，S中的顶点的距离就是从v到此顶点的最短路径长度，U中的顶点的距离，是从v到此顶点只包括S中的顶点为中间顶点的当前最短路径长度。

算法步骤:

• 1.初始时，S只包含起点s；U包含除s外的其他顶点，且U中顶点的距离为"起点s到该顶点的距离"[例如，U中顶点v的距离为(s,v)的长度，然后s和v不相邻，则v的距离为∞]。

• 2.从U中选出"距离最短的顶点k"，并将顶点k加入到S中；同时，从U中移除顶点k。

• 3.更新U中各个顶点到起点s的距离。之所以更新U中顶点的距离，是由于上一步中确定了k是求出最短路径的顶点，从而可以利用k来更新其它顶点的距离；例如，(s,v)的距离可能大于(s,k)+(k,v)的距离。

• 4.重复步骤(2)和(3)，直到遍历完所有顶点。

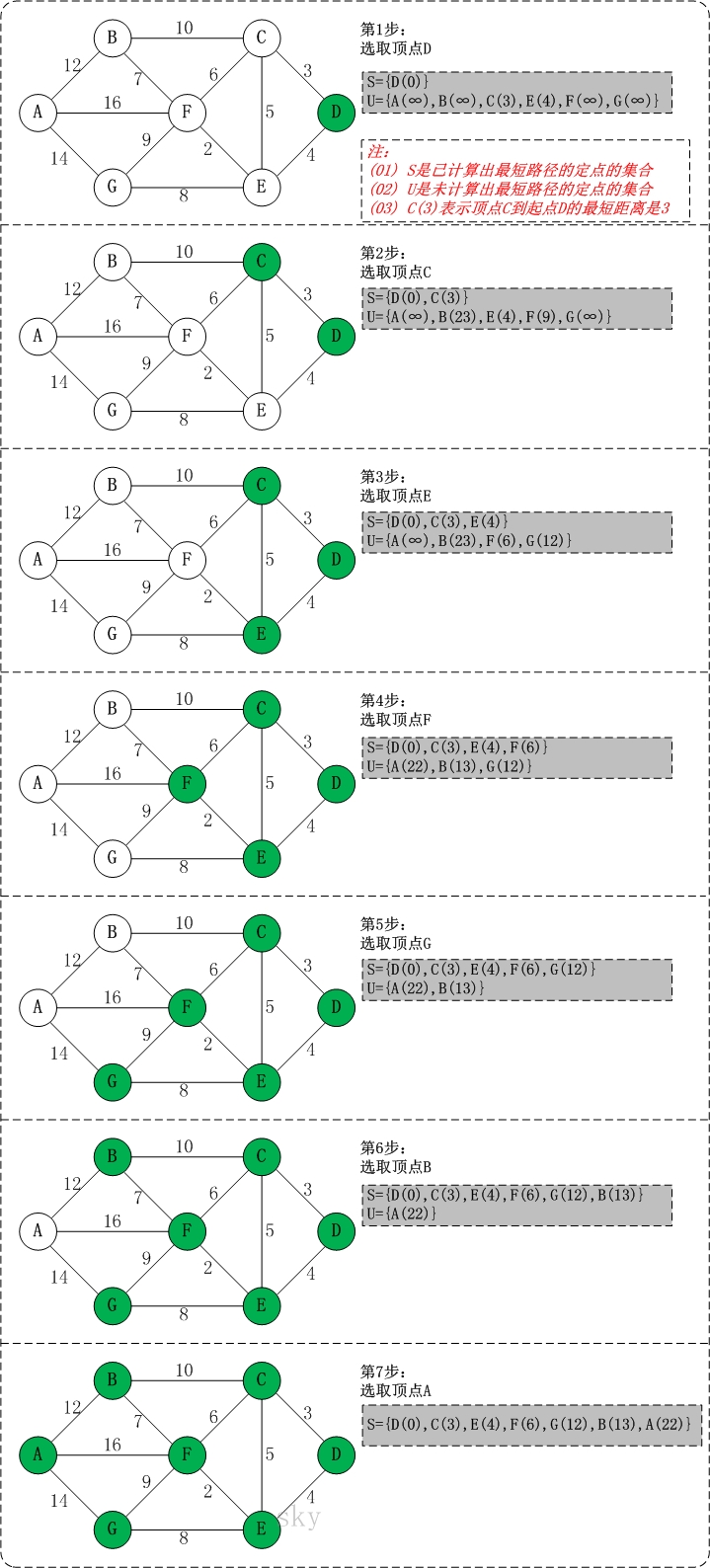
初始状态：S是已计算出最短路径的顶点集合，U是未计算除最短路径的顶点的集合！

第1步：将顶点D加入到S中。 此时，S={D(0)}, U={A(∞),B(∞),C(3),E(4),F(∞),G(∞)}。 注:C(3)表示C到起点D的距离是3。

第2步：将顶点C加入到S中。 上一步操作之后，U中顶点C到起点D的距离最短；因此，将C加入到S中，同时更新U中顶点的距离。以顶点F为例，之前F到D的距离为∞；但是将C加入到S之后，F到D的距离为9=(F,C)+(C,D)。此时，S={D(0),C(3)}, U={A(∞),B(23),E(4),F(9),G(∞)}。

第3步：将顶点E加入到S中。上一步操作之后，U中顶点E到起点D的距离最短；因此，将E加入到S中，同时更新U中顶点的距离。还是以顶点F为例，之前F到D的距离为9；但是将E加入到S之后，F到D的距离为6=(F,E)+(E,D)。此时，S={D(0),C(3),E(4)}, U={A(∞),B(23),F(6),G(12)}。

第4步：将顶点F加入到S中。 此时，S={D(0),C(3),E(4),F(6)}, U={A(22),B(13),G(12)}。

第5步：将顶点G加入到S中。 此时，S={D(0),C(3),E(4),F(6),G(12)}, U={A(22),B(13)}。

第6步：将顶点B加入到S中。 此时，S={D(0),C(3),E(4),F(6),G(12),B(13)}, U={A(22)}。

第7步：将顶点A加入到S中。 此时，S={D(0),C(3),E(4),F(6),G(12),B(13),A(22)}。

算法实现

#include<iostream>
#include<string>
using namespace std;

/*
本程序是使用Dijkstra算法实现求解最短路径的问题
采用的邻接矩阵来存储图
*/
//记录起点到每个顶点的最短路径的信息
struct Dis {
    string path;
    int value;
    bool visit;
    Dis() {
        visit = false;
        value = 0;
        path = "";
    }
};

class Graph_DG {
private:
    int vexnum;   //图的顶点个数
    int edge;     //图的边数
    int **arc;   //邻接矩阵
    Dis * dis;   //记录各个顶点最短路径的信息
public:
    //构造函数
    Graph_DG(int vexnum, int edge);
    //析构函数
    ~Graph_DG();
    // 判断我们每次输入的的边的信息是否合法
    //顶点从1开始编号
    bool check_edge_value(int start, int end, int weight);
    //创建图
    void createGraph();
    //打印邻接矩阵
    void print();
    //求最短路径
    void Dijkstra(int begin);
    //打印最短路径
    void print_path(int);
};
//构造函数
Graph_DG::Graph_DG(int vexnum, int edge) {
    //初始化顶点数和边数
    this->vexnum = vexnum;
    this->edge = edge;
    //为邻接矩阵开辟空间和赋初值
    arc = new int*[this->vexnum];
    dis = new Dis[this->vexnum];
    for (int i = 0; i < this->vexnum; i++) {
        arc[i] = new int[this->vexnum];
        for (int k = 0; k < this->vexnum; k++) {
            //邻接矩阵初始化为无穷大
                arc[i][k] = INT_MAX;
        }
    }
}
//析构函数
Graph_DG::~Graph_DG() {
    delete[] dis;
    for (int i = 0; i < this->vexnum; i++) {
        delete this->arc[i];
    }
    delete arc;
}

// 判断我们每次输入的的边的信息是否合法
//顶点从1开始编号
bool Graph_DG::check_edge_value(int start, int end, int weight) {
    if (start<1 || end<1 || start>vexnum || end>vexnum || weight < 0) {
        return false;
    }
    return true;
}

void Graph_DG::createGraph() {
    cout << "请输入每条边的起点和终点（顶点编号从1开始）以及其权重" << endl;
    int start;
    int end;
    int weight;
    int count = 0;
    while (count != this->edge) {
        cin >> start >> end >> weight;
        //首先判断边的信息是否合法
        while (!this->check_edge_value(start, end, weight)) {
            cout << "输入的边的信息不合法，请重新输入" << endl;
            cin >> start >> end >> weight;
        }
        //对邻接矩阵对应上的点赋值
        arc[start - 1][end - 1] = weight;
        //无向图添加上这行代码
        //arc[end - 1][start - 1] = weight;
        ++count;
    }
}

void Graph_DG::print() {
    cout << "图的邻接矩阵为：" << endl;
    int count_row = 0; //打印行的标签
    int count_col = 0; //打印列的标签
    //开始打印
    while (count_row != this->vexnum) {
        count_col = 0;
        while (count_col != this->vexnum) {
            if (arc[count_row][count_col] == INT_MAX)
                cout << "∞" << " ";
            else
            cout << arc[count_row][count_col] << " ";
            ++count_col;
        }
        cout << endl;
        ++count_row;
    }
}
void Graph_DG::Dijkstra(int begin){
    //首先初始化我们的dis数组
    int i;
    for (i = 0; i < this->vexnum; i++) {
        //设置当前的路径
        dis[i].path = "v" + to_string(begin) + "-->v" + to_string(i + 1);
        dis[i].value = arc[begin - 1][i];
    }
    //设置起点的到起点的路径为0
    dis[begin - 1].value = 0;
    dis[begin - 1].visit = true;

    int count = 1;
    //计算剩余的顶点的最短路径（剩余this->vexnum-1个顶点）
    while (count != this->vexnum) {
        //temp用于保存当前dis数组中最小的那个下标
        //min记录的当前的最小值
        int temp=0;
        int min = INT_MAX;
        for (i = 0; i < this->vexnum; i++) {
            if (!dis[i].visit && dis[i].value<min) {
                min = dis[i].value;
                temp = i;
            }
        }
        //cout << temp + 1 << "  "<<min << endl;
        //把temp对应的顶点加入到已经找到的最短路径的集合中
        dis[temp].visit = true;
        ++count;
        for (i = 0; i < this->vexnum; i++) {
            //注意这里的条件arc[temp][i]!=INT_MAX必须加，不然会出现溢出，从而造成程序异常
            if (!dis[i].visit && arc[temp][i]!=INT_MAX && (dis[temp].value + arc[temp][i]) < dis[i].value) {
                //如果新得到的边可以影响其他为访问的顶点，那就就更新它的最短路径和长度
                dis[i].value = dis[temp].value + arc[temp][i];
                dis[i].path = dis[temp].path + "-->v" + to_string(i + 1);
            }
        }
    }

}
void Graph_DG::print_path(int begin) {
    string str;
    str = "v" + to_string(begin);
    cout << "以"<<str<<"为起点的图的最短路径为：" << endl;
    for (int i = 0; i != this->vexnum; i++) {
        if(dis[i].value!=INT_MAX)
        cout << dis[i].path << "=" << dis[i].value << endl;
        else {
            cout << dis[i].path << "是无最短路径的" << endl;
        }
    }
}
//检验输入边数和顶点数的值是否有效，可以自己推算为啥：
//顶点数和边数的关系是：((Vexnum*(Vexnum - 1)) / 2) < edge
bool check(int Vexnum, int edge) {
    if (Vexnum <= 0 || edge <= 0 || ((Vexnum*(Vexnum - 1)) / 2) < edge)
        return false;
    return true;
}
int main() {
    int vexnum; int edge;

    cout << "输入图的顶点个数和边的条数：" << endl;
    cin >> vexnum >> edge;
    while (!check(vexnum, edge)) {
        cout << "输入的数值不合法，请重新输入" << endl;
        cin >> vexnum >> edge;
    }
    Graph_DG graph(vexnum, edge);
    graph.createGraph();
    graph.print();
    graph.Dijkstra(1);
    graph.print_path(1);
    system("pause");
    return 0;
}

/*
输入：

6 8
1 3 10
1 5 30
1 6 100
2 3 5
3 4 50
4 6 10
5 6 60
5 4 20

*/

参考:

勿在浮沙筑高台

Ouyang_Lianjun-最短路径问题---Dijkstra算法详解