FHQ treap学习（复习）笔记

.....好吧....最后一篇学习笔记的flag它倒了.....

好吧，这篇笔记也鸽了好久好久了...

比赛前刷模板，才想着还是补个坑吧...

FHQ，这个神仙（范浩强大佬），发明了这个神仙的数据结构，

首先，本篇博客使用洛谷普通平衡树为背景，即

• 查找前驱
• 查找后记
• 查找kth的数
• 查找k的排名
• 插入一个数
• 删除一个数

FHQ treap，是一个treap，它还是和treap一样，是tree+heap，所以它也有一个键值维护堆的性质。

它可以干任何treap和Splay能干的事。

它的实现主要由两个函数实现：

merge：把两棵树合并成一棵

split：把树分割成两棵

在这里介绍两个函数的实现方法：

merge

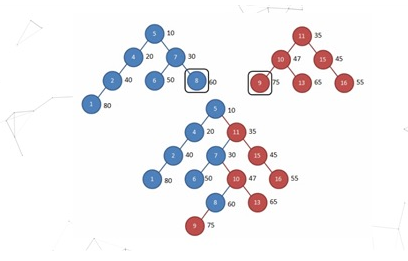
可以看到，它把两棵树合并了起来，但是并不是简单地接起来，而是打散，重新组合。

代码：

int merge(int x,int y)//把xy为根的两棵子树给合并
{
    if(!x||!y)//如果一边没了
    return x+y;//就返回
    if(t[x].key<t[y].key)//维护key值，如果x的key值小于y的k值
    {
        t[x].son[]=merge(t[x].son[],y);//说明此时一定不符合堆性质，把x的右儿子和y合并
        update(x);//更新相关变量
        return x;//返回根节点
    }
    else
    {
        t[y].son[]=merge(x,t[y].son[]);//同上
        update(y);
        return y;
    }
}

通过这样一个递归，不断拆分节点&&合并的过程中，就建立了一棵新树。

split：

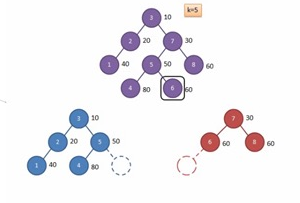
从上图可得：（把树从5分开）

split的过程就是把树拆分成左右树，左树所有节点权值都小于k，右树的节点权值都大于k。

怎么实现呢？

代码：

void split(int now,int k,int &x,int &y)//把一棵树now给从k分割成x和y
{
    if(!now) x=y=;//如果没有了，就返回
    else
    {
        if(t[now].v<=k) //如果当前点的权值小于k，它应该在左子树
        {
            x=now;//更新
            split(t[now].son[],k,t[now].son[],y);分割右儿子，找一个可能的更大的
        }
        else//同上
        {
            y=now;
            split(t[now].son[],k,x,t[now].son[]);
        }
        update(now);
    }
}

这样，我们就可以干以上的事了。

前置：查找kth

因为建立的事一个二叉查找树，所以还是可以像遍历二叉查找树那样查找kth的。

代码十分简单

int kth(int now,int k)
{
    while()
    {
        if(k<=t[t[now].son[]].size)
            now=t[now].son[];
        else
        {
            if(k==t[t[now].son[]].size+)
            return now;
            else
            {
                k-=t[t[now].son[]].size+;
                now=t[now].son[];
            }
        }
    }
}

然后就可以A掉普通平衡树了。

插入新节点：首先暴力新建一个节点

int new_node(int k)
{
    tot++;
    t[tot].size=;
    t[tot].v=k;
    t[tot].key=rand();
    return tot;
}

然后把树从k地方断开，把新节点看做一棵树，把它和上下树合在一起就行了

split(rt,a,x,y);
rt=merge(merge(x,new_node(a)),y);

删除节点：

把树从k断开，然后把左树从k-1断开，然后把上下树给合并，把k节点扔了就行了

split(rt,a,x,z);
split(x,a-,x,y);
y=merge(t[y].son[],t[y].son[]);
rt=merge(merge(x,y),z);

查找排名：

把树从k分开，则k所在的数的size即使排名

split(rt,a-,x,y);
printf("%d\n",t[x].size+);
rt=merge(x,y);

查找kth：

直接用kth函数即可

printf("%d\n",t[kth(rt,a)].v);

前驱：

把树从k分开，则size-1大小的那个kth点就是前驱

split(rt,a-,x,y);
printf("%d\n",t[kth(x,t[x].size)].v);
rt=merge(x,y);

后继：同上

split(rt,a,x,y);
printf("%d\n",t[kth(y,)].v);
rt=merge(x,y);

完整高清无码代码：

#include<bits/stdc++.h>
using namespace std;
const int maxn=1e6+;
struct tree
{
    int son[],v,key,size;
}t[maxn];
int tot=,rt=;
void update(int p)
{
    t[p].size=t[t[p].son[]].size+t[t[p].son[]].size+;
}
int new_node(int k)
{
    tot++;
    t[tot].size=;
    t[tot].v=k;
    t[tot].key=rand();
    return tot;
}
int merge(int x,int y)//o?2￠ò?x￡?y?a?ùμ?á???×óê÷
{
    if(!x||!y)
    return x+y;
    if(t[x].key<t[y].key)
    {
        t[x].son[]=merge(t[x].son[],y);
        update(x);
        return x;
    }
    else
    {
        t[y].son[]=merge(x,t[y].son[]);
        update(y);
        return y;
    }
}
void split(int now,int k,int &x,int &y)//ò?è¨?μk·?à?nowê÷3éx,y
{
    if(!now) x=y=;
    else
    {
        if(t[now].v<=k) //°??ùóDD?óúkμ?è¨?μμ??úμ?·?μ?ò???ê÷?D
        {
            x=now;
            split(t[now].son[],k,t[now].son[],y);
        }
        else
        {
            y=now;
            split(t[now].son[],k,x,t[now].son[]);
        }
        update(now);
    }
}
int kth(int now,int k)
{
    while()
    {
        if(k<=t[t[now].son[]].size)
            now=t[now].son[];
        else
        {
            if(k==t[t[now].son[]].size+)
            return now;
            else
            {
                k-=t[t[now].son[]].size+;
                now=t[now].son[];
            }
        }
    }
}
int x,y,z,n;
int main()
{
    srand((unsigned)time(NULL));
    scanf("%d",&n);
    int flag,a,b,c;
    for(int i=;i<=n;i++)
    {
        scanf("%d",&flag);
        scanf("%d",&a);
        if(flag==)
        {
            split(rt,a,x,y);
            rt=merge(merge(x,new_node(a)),y);
        }
        if(flag==)
        {
            split(rt,a,x,z);
            split(x,a-,x,y);
            y=merge(t[y].son[],t[y].son[]);
            rt=merge(merge(x,y),z);
        }
        if(flag==)
        {
            split(rt,a-,x,y);
            printf("%d\n",t[x].size+);
            rt=merge(x,y);
        }
        if(flag==)
        {
            printf("%d\n",t[kth(rt,a)].v);
        }
        if(flag==)
        {
            split(rt,a-,x,y);
            printf("%d\n",t[kth(x,t[x].size)].v);
            rt=merge(x,y);
        }
        if(flag==)
        {
            split(rt,a,x,y);
            printf("%d\n",t[kth(y,)].v);
            rt=merge(x,y);
        }
    }
    return ;
}