Codeforces D. Powerful array（莫队）

题目描述：

Problem Description

An array of positive integers a1, a2, ..., an is given. Let us consider its arbitrary subarray al, al + 1..., ar, where 1 ≤ l ≤ r ≤ n. For every positive integer s denote by Ks the number of occurrences of s into the subarray. We call the power of the subarray the sum of products Ks·Ks·s for every positive integer s. The sum contains only finite number of nonzero summands as the number of different values in the array is indeed finite.

You should calculate the power of t given subarrays.
Input

First line contains two integers n and t (1 ≤ n, t ≤ 200000) — the array length and the number of queries correspondingly.

Second line contains n positive integers ai (1 ≤ ai ≤ 106) — the elements of the array.

Next t lines contain two positive integers l, r (1 ≤ l ≤ r ≤ n) each — the indices of the left and the right ends of the corresponding subarray.
Output

Output t lines, the i-th line of the output should contain single positive integer — the power of the i-th query subarray.

Please, do not use %lld specificator to read or write 64-bit integers in C++. It is preferred to use cout stream (also you may use %I64d).
Examples

Input

3 2
1 2 1
1 2
1 3

Output

3
6

Input

8 3
1 1 2 2 1 3 1 1
2 7
1 6
2 7

Output

20
20
20
Note

Consider the following array (see the second sample) and its [2, 7] subarray (elements of the subarray are colored):

Then K1 = 3, K2 = 2, K3 = 1, so the power is equal to 32·1 + 22·2 + 12·3 = 20.

思路：

题目是要求给定一个区间，分别统计出区间不同数字的个数，对每个不同的数，求出现次数的平方与该数字的乘积的和。

因为给了好几组区间，很容易想到是一种直接暴力的算法，每个询问都统计一次然后算出一个ans来，但很显然这个算法会超时，因为对于不同的询问区间可能会有一部分重合的以求得的信息，每次暴力计算并没有利用这些已知信息。那么如何使用呢？想到既然是区间问题那不如用线段树来维护一个区间，但是，对于蒟蒻来说，我会做的线段树只能维护一些简单的信息，不会维护这种复杂的统计信息（我还是太菜了），怎么办呢？要知道，维护区间信息问题还有一种重要且巧妙的方法——莫队算法。

哈哈哈，知道了这个算法，虽然也是暴力算法，但是它通过分块+排序预处理能把复杂度降到O(n*sqrt(n))，就可以做了。注意在处理ans是改动一下就好

小心的是，如果用的分组方法是这种：就千万小心把belong数组开大一点，（两倍就行），因为它是刚好分成size*bulk，这么多元素，如果测试点是2e5（对这道题而言），那么最后belong原来的空间用完后会继续往下面的位置赋值，导致越界。（我在这卡了好久qwq）。还有cnt统计个数数组不能开long long。

     for(int i = ;i<=bulk;i++)
     {
         for(int j = (i-)*size+;j<=i*size;j++)
         {
             belong[j] = i;
         }
     }

（bulk是块数，size是每块的大小）

当然，下面这种分组方式就不存在问题，因为他刚好分n个元素。

 for(int i = ;i<=n;i++)
 scanf("%d",&col[i]),Be[i]=i/unit+;

卡常技巧：

cmp函数改为莫队玄学奇偶性排序（代码中的cmp2），实际上可以帮你每个点平均优化200ms（可怕）

如果允许，吸氧也是极好的#pragma GCC optimize(2)

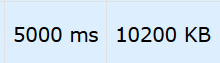
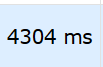
优化结果：

第一个为什么都不做（超时）

第二个为改cmp

第三个为改cmp+开optimize(2)

代码：

 #include <iostream>
 #include <algorithm>
 #include <cmath>
 #define max_n 200005
 using namespace std;
 int a[max_n];
 int cnt[];
 int belong[max_n*];
 int bulk;
 int size;
 long long ans = ;
 long long sum[max_n];
 int n;
 int m;
 struct node
 {
     int r;
     int l;
     int id;
 }q[max_n];
 int cmp(node a,node b)
 {
     return (belong[a.l]==belong[b.l])?a.r<b.r:a.l<b.l;
 }
 int cmp2(node a,node b)
 {
     return (belong[a.l]^belong[b.l])?(a.l<b.l):(belong[a.l]&)?a.r<b.r:a.r>b.r;
 }

 void add(int pos)
 {
     ans -= (long long)a[pos]*cnt[a[pos]]*cnt[a[pos]];
     /*if(cnt[a[pos]]==0)
     {
         ans++;
     }*/
     cnt[a[pos]]++;
     ans += (long long)a[pos]*cnt[a[pos]]*cnt[a[pos]];
 }
 void del(int pos)
 {
     ans -= (long long)a[pos]*cnt[a[pos]]*cnt[a[pos]];
     cnt[a[pos]]--;
     /*if(cnt[a[pos]]==0)
     {
         ans--;
     }*/
     ans += (long long)a[pos]*cnt[a[pos]]*cnt[a[pos]];
 }
 #pragma GCC optimize(2)
 int main()
 {
     cin >> n >> m;
     size = sqrt((double)n);
     bulk = ceil((double)n/size);
     for(int i = ;i<=bulk;i++)
     {
         for(int j = (i-)*size;j<=i*size;j++)
         {
             belong[j] = i;
         }
     }
     for(int i = ;i<=n;i++)
     {
         cin >> a[i];
     }

     for(int i = ;i<=m;i++)
     {
         cin >> q[i].l >> q[i].r;
         q[i].id = i;
     }
     sort(q+,q+m+,cmp2);
     /*for(int i = 0;i<n;i++)
     {
         cout << belong[i] << " ";
     }
     cout << endl;*/
     int l = ;
     int r = ;
     for(int i = ;i<=m;i++)
     {
         int nl = q[i].l;
         int nr = q[i].r;
         while(l>nl) add(--l);
         while(r<nr) add(++r);
         while(l<nl) del(l++);
         while(r>nr) del(r--);
         //cout << q[i].id << endl;
         sum[q[i].id] = ans;
     }
     for(int i = ;i<=m;i++)
     {
         cout << sum[i] << endl;
     }
     return ;
 }

参考文章：

hzwer，「分块」数列分块入门1 – 9 by hzwer，http://hzwer.com/8053.html（分块算法）

WAMonster，莫队算法——从入门到黑题，https://www.cnblogs.com/WAMonster/p/10118934.html（莫队算法良心讲解）

大米饼，莫队算法，https://www.cnblogs.com/Paul-Guderian/p/6933799.html（莫队算法清晰简明讲解）

（两篇结合互补食用效果为佳）