改进初学者的PID-微分冲击

　　最近看到了Brett Beauregard发表的有关PID的系列文章，感觉对于理解PID算法很有帮助，于是将系列文章翻译过来！在自我提高的过程中，也希望对同道中人有所帮助。作者Brett Beauregard的原文网址：http：//brettbeauregard.com/blog/2011/04/improving-the-beginner%E2%80%99s-pid-derivative-kick/

1、问题

　　这个修改将稍微调整微分项。其目标是消除一种被称为“微分冲击”的现象。

　　上图说明了问题。由于error = Setpoint-Input，设定值的任何变化都会导致偏差的瞬时变化。这种变化的导数是无穷大（实际上，由于dt不是0，它只是一个非常大的数字。）这个数字被输入PID方程，这导致输出中出现不希望的峰值。幸运的是，有一种简单的方法可以摆脱这种情况。

2、解决方案

　　事实证明，当设定值发生变化时，偏差的导数等于输入的负导数。这最终成为一个完美的解决方案。我们减去（Kd *输入的导数）而不是添加（Kd *偏差的导数）。这被称为使用“基于测量的微分”。

3、代码

 /*working variables*/
 unsigned long lastTime;
 double Input，Output，Setpoint;
 double errSum，lastInput;
 double kp，ki，kd;
 int SampleTime = ; //1 sec
 void Compute()
 {
    unsigned long now = millis();
    int timeChange = (now - lastTime);
    if(timeChange>=SampleTime)
    {
       /*Compute all the working error variables*/
       double error = Setpoint - Input;
       errSum += error;
       double dInput = (Input - lastInput);

       /*Compute PID Output*/
       Output = kp * error + ki * errSum - kd * dInput;

       /*Remember some variables for next time*/
       lastInput = Input;
       lastTime = now;
    }
 }

 void SetTunings(double Kp，double Ki，double Kd)
 {
   double SampleTimeInSec = ((double)SampleTime)/;
    kp = Kp;
    ki = Ki * SampleTimeInSec;
    kd = Kd / SampleTimeInSec;
 }

 void SetSampleTime(int NewSampleTime)
 {
    if (NewSampleTime > )
    {
       double ratio  = (double)NewSampleTime
                       / (double)SampleTime;
       ki *= ratio;
       kd /= ratio;
       SampleTime = (unsigned long)NewSampleTime;
    }
 }

　　这里的修改非常简单。我们用-dInput替换+ dError。我们现在需要记住lastInput，而不是记住lastError

4、结果

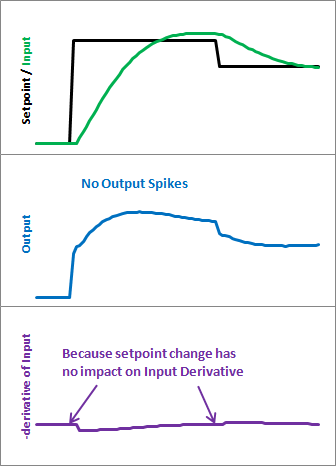
　　以下是这些修改对我们的影响。请注意，输入看起来仍然相同。所以我们得到相同的性能，但是每次设定点改变时我们都不会发出巨大的输出尖峰。

　　这也许没什么大不了的。这完全取决于应用程序对输出峰值有多敏感。但在我看来，没有冲击就不需要做更多的工作，所以为什么不把事情做好呢?

欢迎关注：