西门子PLC1200内使用SCL实现简化版PID算法

西门子自带的PID效果很好，但是会比较吃性能，使用次数有限，很多地方需要PID但不需要这么精准的PID，所以网上找个简单的算法自己调用。

新建数据类型

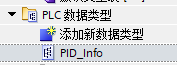
前三个就是PID三个参数

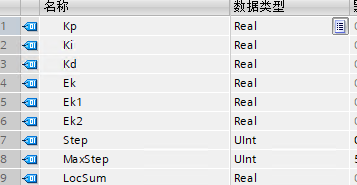
新建FC块:

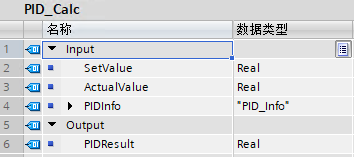
#PIDInfo.Step += ;
IF #PIDInfo.Step >= #PIDInfo.MaxStep- THEN
    #PIDInfo.Step := ;
    #PIDInfo.Ek := #SetValue - #ActualValue;
    #PIDInfo.LocSum += #PIDInfo.Ek;          //累计误差
    #PIDResult := #PIDInfo.Kp * #PIDInfo.Ek + (#PIDInfo.Ki * #PIDInfo.LocSum) + #PIDInfo.Kd * (#PIDInfo.Ek1 - #PIDInfo.Ek);
    #PIDInfo.Ek1 := #PIDInfo.Ek;
END_IF;

调用：

DB块内增加变量

Step和MaxStep用于控制扫描多少次调用一次，以及可以错开调用

左边填入设置值，实际值，和刚才添加的变量，右边输出PID，PID输出值没有明确的范围，自己用Limite限制范围，调整P值让输出值在范围内浮动

附C#实现

class PID_Info
    {
        float Kp = ;                       //比例系数Proportional
        float Ki = 0.2f;                       //积分系数Integral
        float Kd = 0.1f;                       //微分系数Derivative

        float Ek;                       //当前误差
        float Ek1;                      //前一次误差 e(k-1)
        float Ek2;                      //再前一次误差 e(k-2)
        float LocSum;                   //累计积分位置

        public static float PID_Calc1(float SetValue, float ActualValue, PID_Info PID)
        {
            float PIDLoc;                                  //位置

            PID.Ek = SetValue - ActualValue;
            PID.LocSum += PID.Ek;                         //累计误差

            PIDLoc = PID.Kp * PID.Ek + (PID.Ki * PID.LocSum) + PID.Kd * (PID.Ek1 - PID.Ek);

            PID.Ek1 = PID.Ek;
            return PIDLoc;
        }

        public float Calc1(float SetValue, float ActualValue)
        {
            return PID_Calc1(SetValue, ActualValue, this);
        }

        public static float PID_Inc(float SetValue, float ActualValue, PID_Info PID)
        {
            float PIDInc;                                  //增量

            PID.Ek = SetValue - ActualValue;
            PIDInc = (PID.Kp * PID.Ek) - (PID.Ki * PID.Ek1) + (PID.Kd * PID.Ek2);

            PID.Ek2 = PID.Ek1;
            PID.Ek1 = PID.Ek;
            return PIDInc;
        }

        public float Inc(float SetValue, float ActualValue)
        {
            return PID_Inc(SetValue, ActualValue, this);
        }
    }

算法来自

blog。csdn。net/weibo1230123/article/details/80812211