Hermite （埃尔米特）曲线

Hermite 曲线

　　已知曲线的两个端点坐标P0、P1，和端点处的切线R0、R1，确定的一条曲线。

参数方程

　　1. 几何形式

　　

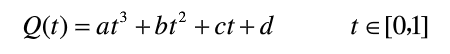
　　2. 矩阵形式

　　　

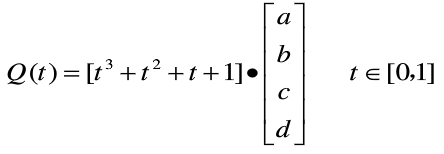
　　3. 推导

　　　　

　　

　　

　　

　　

　　

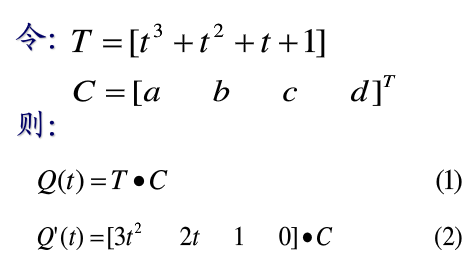
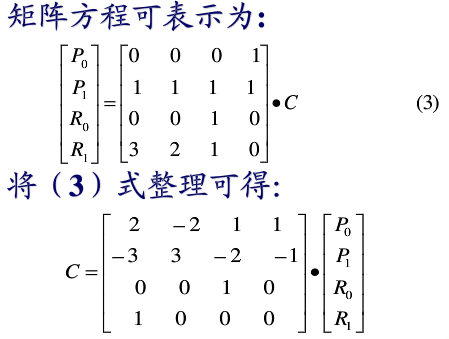
例子分析

　　

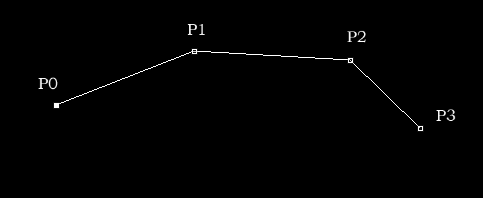
　　如上图有四个点，假如P0、P2是端点，那么向量R0=(P1-P0)，R1=(P3-P2)，将数据带入调和函数，即求得曲线。

　　在程序中，我们通常会使用特殊方法处理顶点之间的关系。

　　

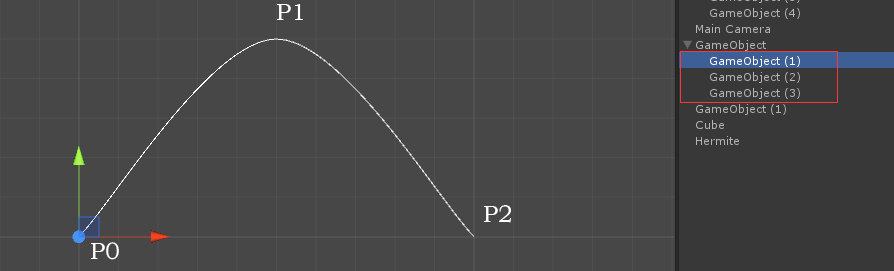
　　图中含有3个顶点，我们把每挨着的两个顶点看做是一条Hermite曲线，P0和P1是两个端点，那么现在，我们如何求得R1呢？ 我们现在构建连个参考点F1,F2。

　　　　令  F1 = P0; 　　F2 = P2;

　　　　那么 R1 = P1-F1;　　R2 = F2-P1;

　　然后将此值带入曲线函数，即可为求得的曲线。　　

程序代码

该代码是Unity脚本代码:

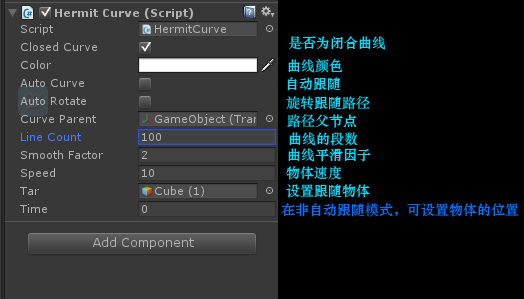
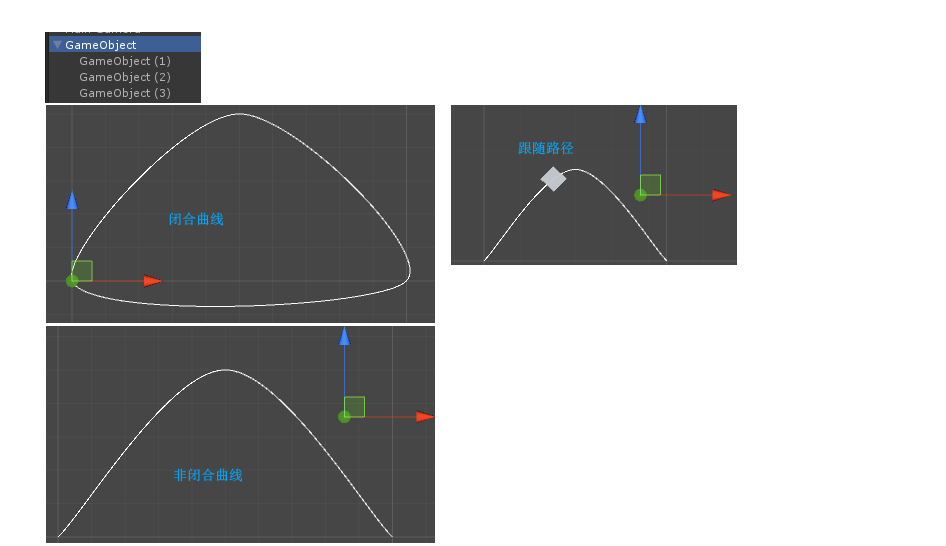
　　1. 实现编辑器闭合曲线和非闭合曲线的绘制；

　　2. 运行脚本，可以实现物体跟随曲线路径移动，可以勾选旋转跟随与不跟随；

　　3. 如果不进行自动跟随曲线路径，可以修改时间值，移动物体。

using UnityEngine;
using System.Collections;
using System.Collections.Generic;
public class HermitCurve : Curve_Root {

    public Transform CurveParent;
    public int lineCount;
    private List<NodePath> nodePath;
    public float smoothFactor = 2.0f;

    private Transform[] transforms;
    private Vector3[] node;
    public float Speed = 10.0f;

    Vector3 curPos;
    Vector3 nextPos;
    Quaternion curRotate;
    Quaternion nextRotate;
    float moveTime;
    float curTime;
    public GameObject Tar;
    int index;
    private Transform T;

    public float time;

    /// <summary>
    /// 数据校正
    /// </summary>
    void DadaCorrection()
    {
        //根节点验证
        if (CurveParent == null)
        {
            Debug.LogError("Please add curve the root node.");
            return;
        }

        //修正平滑因子： 2时，较为理想。
        smoothFactor = smoothFactor >= 10.0f ? 10.0f : smoothFactor;
        smoothFactor = smoothFactor <= 1.0f ? 1.0f : smoothFactor;
    }

    /// <summary>
    /// 计算路径节点
    /// </summary>
    void ComputeNode()
    {
        //将节点添加入链表
        Component[] mTrans = CurveParent.GetComponentsInChildren(typeof(Transform));//物体和子物体的Trans
        if (mTrans.Length -  < )
        {
            Debug.LogError("Please add at least two points.");
            return;
        }

        //非闭合曲线与闭合曲线的顶点时间计算：非闭合曲线，最后个顶点的时间为1.0，闭合曲线的最后个顶点的时间为倒数第二个顶点，因为他的最后个点是原点。
        float t;
        if (closedCurve)
        {
            t = 1.0f / (mTrans.Length - );
            nodePath = new List<NodePath>();
            for (int i = ; i < mTrans.Length; i++)//根节点不参与路径节点的计算
            {
                nodePath.Add(new NodePath(mTrans[i].transform.position, (i - ) * t));
            }
            //闭合曲线完整的节点
            AddClosedCurveNode();
        }
        else
        {
            t = 1.0f / (mTrans.Length - );
            nodePath = new List<NodePath>();
            for (int i = ; i < mTrans.Length; i++)//根节点不参与路径节点的计算
            {
                nodePath.Add(new NodePath(mTrans[i].transform.position, (i - ) * t));
            }
            //非闭合曲线完整的节点
            AddCurveNode();
        }
    }

    // Use this for initialization
    void Start () {

        DadaCorrection();

        ComputeNode();

        node = new Vector3[lineCount+];
        //Vector3 start = nodePath[1].point;
        //Vector3 end;

        node[] = nodePath[].point;
        Vector3 end;
        //绘制节点
        for (int i = ; i <= lineCount; i++)
        {
            float ti = i / (float)lineCount;
            end = GetHermitAtTime(ti);
            if (node != null)
            {
                node[i] = end;
            }
        }

        T = new GameObject().transform;

        curPos = node[];
        nextPos = node[];
        moveTime = (nextPos - curPos).magnitude / Speed;

        Tar.transform.position = curPos;
        Tar.transform.transform.LookAt(nextPos);
        curRotate = Tar.transform.rotation;
        T.position = node[];
        T.LookAt(node[]);
        nextRotate = T.rotation;
        curTime = ;
        index = ;
    }

    // Update is called once per frame
    void Update () {

        if (AutoCurve)
        {
            if (moveTime > curTime)
            {
                Tar.transform.position = Vector3.Lerp(curPos, nextPos, curTime / moveTime);
                if (AutoRotate)
                {
                    Tar.transform.rotation = Quaternion.Slerp(curRotate, nextRotate, curTime / moveTime);
                }

                curTime += Time.deltaTime;
            }
            else
            {
                if (closedCurve)
                {
                    index = ((index + ) % (lineCount + ) == ) ?  : index + ;
                }
                else
                {
                    index = ((index + ) % (lineCount+) == ) ? index : index + ;
                }
                curPos = nextPos;
                nextPos = node[index];

                curTime = ;
                moveTime = (nextPos - curPos).magnitude / Speed;

                T.position = node[index];
                curRotate = nextRotate;

                if (closedCurve)
                {
                    int c1;
                    if (index == node.Length-)
                    {
                        c1 = ;
                    }
                    else
                    {
                        c1 = index + ;
                    }
                    T.LookAt(node[c1]);
                }
                else
                {
                    int c1;
                    if (index == node.Length - )
                    {
                        c1 = ;
                    }
                    else
                    {
                        c1 = index + ;
                        T.LookAt(node[c1]);
                    }
                }

                nextRotate = T.rotation;
            }
        }
        else
        {
            if (closedCurve)
            {
                if (AutoRotate)
                {
                    time = time > 1.0f ? 0.0f : time;
                    time = time < 0.0f ? 1.0f : time;
                    Vector3 cur = GetHermitAtTime(time);
                    Tar.transform.position = cur;

                    float del = 1.0f / lineCount;
                    Vector3 next0 = GetHermitAtTime(time + del);
                    Tar.transform.LookAt(next0);
                }
                else
                {
                    time = time > 1.0f ? 0.0f : time;
                    time = time < 0.0f ? 1.0f : time;
                    Vector3 cur = GetHermitAtTime(time);
                    Tar.transform.position = cur;
                }
            }
            else
            {
                if (AutoRotate)
                {
                    time = time > 1.0f ? 1.0f : time;
                    time = time < 0.0f ? 0.0f : time;
                    Vector3 cur = GetHermitAtTime(time);
                    Tar.transform.position = cur;

                    float del = 1.0f / lineCount;
                    Vector3 next0 = GetHermitAtTime(time + del);

                    Tar.transform.LookAt(next0);
                }
                else
                {
                    time = time > 1.0f ? 1.0f : time;
                    time = time < 0.0f ? 0.0f : time;
                    Vector3 cur = GetHermitAtTime(time);
                    Tar.transform.position = cur;
                }
            }

        }

    }

    /// <summary>
    /// 绘制曲线
    /// </summary>
    void DrawCurve()
    {
        if (closedCurve)
        {
            Vector3 start = nodePath[].point;
            Vector3 end;

            Gizmos.color = _Color;
            //绘制节点
            for (int i = ; i < lineCount; i++)
            {
                float time = i / (float)lineCount;
                end = GetHermitAtTime(time);
                //Debug.Log(end);
                Gizmos.DrawLine(start, end);

                start = end;
            }
            Gizmos.DrawLine(start, nodePath[nodePath.Count - ].point);
        }
        else
        {
            Vector3 start = nodePath[].point;
            Vector3 end;

            Gizmos.color = _Color;
            //绘制节点
            for (int i = ; i < lineCount; i++)
            {
                float time = i / (float)lineCount;
                end = GetHermitAtTime(time);
                //Debug.Log(end);
                Gizmos.DrawLine(start, end);
                start = end;
            }
            Gizmos.DrawLine(start, nodePath[nodePath.Count - ].point);
        }
    }

    /// <summary>
    /// 在Scene场景中，绘制Hermite曲线
    /// </summary>
    void OnDrawGizmos()
    {
        /*数据校正*/
        DadaCorrection();
        /*计算顶点*/
        ComputeNode();
        /*计算曲线*/
        DrawCurve();
    }

    /// <summary>
    /// 1. 非闭合曲线
    /// </summary>
    public void AddCurveNode()
    {
        nodePath.Insert(, nodePath[]);
        nodePath.Add(nodePath[nodePath.Count - ]);
    }

    /// <summary>
    /// 2. 闭合曲线
    /// </summary>
    public void AddClosedCurveNode()
    {
        //nodePath.Insert(0, nodePath[0]);
        nodePath.Add(new NodePath(nodePath[]));
        nodePath[nodePath.Count - ].time = 1.0f;

        Vector3 vInitDir = (nodePath[].point - nodePath[].point).normalized;
        Vector3 vEndDir = (nodePath[nodePath.Count - ].point - nodePath[nodePath.Count - ].point).normalized;
        float firstLength = (nodePath[].point - nodePath[].point).magnitude;
        float lastLength = (nodePath[nodePath.Count - ].point - nodePath[nodePath.Count - ].point).magnitude;

        NodePath firstNode = new NodePath(nodePath[]);
        firstNode.point = nodePath[].point + vEndDir * firstLength;

        NodePath lastNode = new NodePath(nodePath[nodePath.Count - ]);
        lastNode.point = nodePath[].point + vInitDir * lastLength;

        nodePath.Insert(, firstNode);
        nodePath.Add(lastNode);
    }

    /// <summary>
    /// 通过节点段数的时间大小，获取每段节点
    /// </summary>
    /// <param name="t"></param>
    /// <returns></returns>
    public Vector3 GetHermitAtTime(float t)
    {
        //Debug.Log(t);
        int k;
        //最后一个顶点
        if (t >= nodePath[nodePath.Count - ].time)
        {
            return nodePath[nodePath.Count - ].point;
        }
        for (k = ; k < nodePath.Count-; k++)
        {
            if (nodePath[k].time > t)
                break;
        }

        k = k - ;
        float param = (t - nodePath[k].time) / (nodePath[k+].time - nodePath[k].time);
        return GetHermitNode(k, param);
    }

    /// <summary>
    /// Herimite曲线：获取节点
    /// </summary>
    /// <param name="index">节点最近的顶点</param>
    /// <param name="t"></param>
    /// <returns></returns>
    public Vector3 GetHermitNode(int index,float t)
    {
        Vector3 v;
        Vector3 P0 = nodePath[index - ].point;
        Vector3 P1 = nodePath[index].point;
        Vector3 P2 = nodePath[index + ].point;
        Vector3 P3 = nodePath[index + ].point;

        //调和函数
        float h1 =  * t * t * t -  * t * t + ;
        float h2 = - * t * t * t +  * t * t;
        float h3 = t * t * t -  * t * t + t;
        float h4 = t * t * t - t * t;

        v = h1 * P1 + h2 * P2 + h3 * (P2 - P0) / smoothFactor + h4 * (P3 - P1) / smoothFactor;
        //Debug.Log(index + "  "+ t+"  "+v);
        return v;
    }
}

/// <summary>
/// 节点类
/// </summary>
public class NodePath
{
    public Vector3 point;
    public float time;

    public NodePath(Vector3 v,float t)
    {
        point = v;
        time = t;
    }

    public NodePath(NodePath n)
    {
        point = n.point;
        time = n.time;
    }
}

基类代码

using UnityEngine;
using System.Collections;

public class Curve_Root : MonoBehaviour {

    //曲线是否为闭合曲线
    public bool closedCurve = false;

    //曲线的颜色
    public Color _Color = Color.white;

    //自动跟随路径
    public bool AutoCurve = false;

    //旋转跟随
    public bool AutoRotate = false;
}

路径漫游

　　在曲线函数中，参数t取值[0,1]，将曲线进行分段。那么能够计算出每一个点的位置。因此，在路径漫游中，我们从原点出发，将t的增量作为下一个点位置，进行插值移动。就实现了路径漫游，同时进行朝向下一个顶点旋转，就可以使看的方向随着曲线变化。

Unity 3D 项目工程

http://download.csdn.net/detail/familycsd000/9365859