CF Destroying Roads (最短路)

Destroying Roads

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

In some country there are exactly n cities and m bidirectional roads connecting the cities. Cities are numbered with integers from 1 to n. If cities a and b are connected by a road, then in an hour you can go along this road either from city a to city b, or from city b to city a. The road network is such that from any city you can get to any other one by moving along the roads.

You want to destroy the largest possible number of roads in the country so that the remaining roads would allow you to get from city s1 to city t1 in at most l1 hours and get from city s2 to city t2 in at most l2 hours.

Determine what maximum number of roads you need to destroy in order to meet the condition of your plan. If it is impossible to reach the desired result, print -1.

Input

The first line contains two integers n, m (1 ≤ n ≤ 3000, 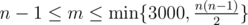) — the number of cities and roads in the country, respectively.

Next m lines contain the descriptions of the roads as pairs of integers ai, bi (1 ≤ ai, bi ≤ n, ai ≠ bi). It is guaranteed that the roads that are given in the description can transport you from any city to any other one. It is guaranteed that each pair of cities has at most one road between them.

The last two lines contains three integers each, s1, t1, l1 and s2, t2, l2, respectively (1 ≤ si, ti ≤ n, 0 ≤ li ≤ n).

Output

Print a single number — the answer to the problem. If the it is impossible to meet the conditions, print -1.

Sample test(s)

input

5 4
1 2
2 3
3 4
4 5
1 3 2
3 5 2

output

0

input

5 4
1 2
2 3
3 4
4 5
1 3 2
2 4 2

output

1

input

5 4
1 2
2 3
3 4
4 5
1 3 2
3 5 1

output

-1

用dijkstra把每个点都跑一遍，求出任意点之间的最短路，然后先假设两条路之间没重叠，那么可以拆的路就是M - 最短路a - 最短路b，再假设有重叠，枚举他们重叠的段。要注意有可能出现起点和终点要互换的情况。

 #include <bits/stdc++.h>
 using    namespace    std;

 const    int    INF = 0xfffffff;
 const    int    SIZE = ;
 int    N,M,D[SIZE][SIZE];
 int    s_1,t_1,l_1,s_2,t_2,l_2;
 bool    S[SIZE];
 struct    Q_Node
 {
     int    d,vec;
     bool    operator <(const Q_Node & r)    const
     {
         return    d > r.d;
     };
 };
 vector<int>    G[SIZE];

 void    dijkstra(int);
 int    main(void)
 {
     int    from,to;

     scanf("%d%d",&N,&M);
     for(int i = ;i < M;i ++)
     {
         scanf("%d%d",&from,&to);
         G[from].push_back(to);
         G[to].push_back(from);
     }
     for(int i = ;i <= N;i ++)
         dijkstra(i);

     scanf("%d%d%d",&s_1,&t_1,&l_1);
     scanf("%d%d%d",&s_2,&t_2,&l_2);
     if(D[s_1][t_1] > l_1 || D[s_2][t_2] > l_2)
     {
         puts("-1");
         return    ;
     }

     int    min = D[s_1][t_1] + D[s_2][t_2];
     int    ans = ;
     for(int i = ;i <= N;i ++)
         for(int j = ;j <= N;j ++)
         {
             if(min > D[s_1][i] + D[s_2][i] + D[i][j] + D[j][t_1] + D[j][t_2])
                 if(D[s_1][i] + D[i][j] + D[j][t_1] <= l_1 &&
                    D[s_2][i] + D[i][j] + D[j][t_2] <= l_2)
                     min = D[s_1][i] + D[s_2][i] + D[i][j] + D[j][t_1] + D[j][t_2];
             if(min > D[t_1][i] + D[t_2][i] + D[i][j] + D[j][s_1] + D[j][s_2])
                 if(D[t_1][i] + D[i][j] + D[j][s_1] <= l_1 &&
                    D[t_2][i] + D[i][j] + D[j][s_2] <= l_2)
                     min = D[t_1][i] + D[t_2][i] + D[i][j] + D[j][s_1] + D[j][s_2];
             if(min > D[t_1][i] + D[s_2][i] + D[i][j] + D[j][s_1] + D[j][t_2])
                 if(D[t_1][i] + D[i][j] + D[j][s_1] <= l_1 &&
                    D[s_2][i] + D[i][j] + D[j][t_2] <= l_2)
                     min = D[t_1][i] + D[s_2][i] + D[i][j] + D[j][s_1] + D[j][t_2];
             if(min > D[s_1][i] + D[t_2][i] + D[i][j] + D[j][t_1] + D[j][s_2])
                 if(D[s_1][i] + D[i][j] + D[j][t_1] <= l_1 &&
                    D[t_2][i] + D[i][j] + D[j][s_2] <= l_2)
                     min = D[s_1][i] + D[t_2][i] + D[i][j] + D[j][t_1] + D[j][s_2];
         }
     printf("%d\n",M - min);

     return    ;
 }

 void    dijkstra(int s)
 {
     priority_queue<Q_Node>    que;
     Q_Node    temp;
     for(int i = ;i <= N;i ++)
     {
         D[s][i] = INF;
         S[i] = false;
     }
     D[s][s] = ;
     temp.d = ;
     temp.vec = s;
     que.push(temp);

     while(!que.empty())
     {
         int    cur = que.top().vec;
         que.pop();
         S[cur] = true;

         for(int i = ;i < G[cur].size();i ++)
             if(!S[G[cur][i]] && D[s][G[cur][i]] > D[s][cur] + )
             {
                 D[s][G[cur][i]] = D[s][cur] + ;
                 temp.vec = G[cur][i];
                 temp.d = D[s][G[cur][i]];
                 que.push(temp);
             }
     }
 }