非负矩阵分解（1）：准则函数及KL散度

作者：桂。

时间：2017-04-06  12:29:26

链接：http://www.cnblogs.com/xingshansi/p/6672908.html

声明：欢迎被转载，不过记得注明出处哦~

---

前言

之前在梳理最小二乘的时候，矩阵方程有一类可以利用非负矩阵分解（Non-negative matrix factorization, NMF）的方法求解，经常见到别人提起这个算法，打算对此梳理一下。优化问题求解，最基本的是问题描述与准则函数的定义，紧接着才涉及准则函数的求解问题，本文为NMF系列第一篇，主要梳理：

　　1）矩阵方程基本问题；

　　2）准则函数定义；

内容为自己的学习总结，其中多有借鉴他人的地方，最后一并给出链接。

一、矩阵方程基本问题

本段描述NMF对应的基本问题。

许多问题都可以建模成矩阵方程：

${\bf{AS}} = {\bf{X}}$

其中根据向量和矩阵的不同，矩阵方程的求解主要分为以下三类问题：

1）超定矩阵方程；m>n，$\bf{X}$和$\bf{A}$均已知，其中之一或二者可能存在观测误差、干扰；

2）盲矩阵方程：仅向量$\bf{X}$已知，矩阵$\bf{A}$未知；

3）欠定稀疏矩阵方程：m<n，$\bf{X}$和$\bf{A}$均已知.

每一类问题，都有对应的方法：如对于盲矩阵方程，由于只有观测向量$\bf{X}$，因此引入误差的时候只能假设观测向量存在误差，而不会像最小二乘那样分为普通最小二乘、数据最小二乘、总体最小二乘。给出矩阵方程及对应求解的示意图：

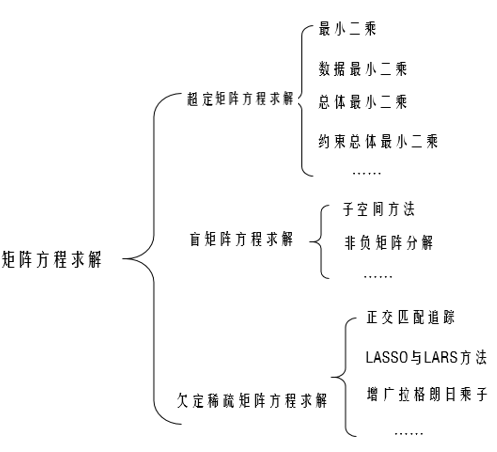
其实${\bf{AS}} = {\bf{X}}$仅仅是一个线性表达，求解本身没有非负的限制。但对于现实中很多应用：比如一张图片，可以认为它由鼻子、眼睛、眉毛...等等拼成，每一个成分对应一些像素值，而这些理论上都应该是非负的，因此在一些矩阵求解问题中，我们希望加入非负的限制。本系列文章主要针对其中的：盲矩阵方程求解——非负矩阵分解算法。

二、准则函数定义

这里只分析最常用的两类准则函数，对于广义AB-散度不作讨论。假设非负矩阵${\bf{X}}$可以分解成：

${\bf{AS}} = {\bf{X}}$

由于观测数据${\bf{X}}$难免带来误差，因此有：

${\bf{X}} = {\bf{AS}}  + \bf{N}$

针对误差最小化，引入准则函数：

下面分析准则函数$D\left( {{\bf{X}}|{\bf{AS}}} \right)$.

　　A-平方欧几里得（Euclidean）距离

当假设误差服从正态分布时，此时的最大似然估计与最小二乘等价，此时对应的准则函数为平方Euclidean距离，有时为了求导方便常添加比例系数1/2：

　　B-Kullback-Leibler（KL）散度

1-KL定义

首先给出KL散度定义：

KL散度与Euclidean距离不同，是非对称的。

2-KL的含义

KL不像Euclidean那么直观，这就有了一个疑问？这么古怪的家伙是从哪冒出来的？

下面一点点理解。

从图中很容易求解$(x_0,y_0)$处的切线方程，其实$x$如果接近$x_0$，这就是一阶Taylor近似，写成更一般的形式：

一阶Taylor逼近的误差则定义为：

推广开来这就是Bregman距离：

令$\phi $:为定义在闭合凸集的一连续可微分凸函数。与函数$\phi $对应的两个向量：之间的Bregman距离记作：，定义为：

如果$\phi $取凸函数：

其实如果$x_i$看作是概率密度，这个就是熵的表达式啊，也就是这里函数调用熵的形式。此时，Bregman距离对应的就是Kullback-Leibler散度，也叫信息散度、信息增益、相对熵、I散度。

从而可以得到：

对号入座，同样可以得出准则函数：

这样一来，KL散度的实际意义就比较明显了：它表达了不同信息熵一阶Taylor的近似，如果细究，二阶、三阶....Taylor近似同样可以得出。

3-KL对应分布

Euclidean距离对应：误差服从正态分布，KL散度是不是也该对应某种分布？答案是当然——泊松分布。泊松分布前面有文章分析过。泊松分布就常见的计数过程，描述的是一段时间事件发生的次数，与它关联较大的一个是二项分布，一个是指数分布。不过这里分析完之后，是不是该多出一个疑问：泊松分布与信息熵有何关系？下面说说泊松分布为什么可以对应KL散度。

给出泊松分布的定义：

从而对于两个分布：

概率相比并取对数：

已经有点KL散度的味道了，因为$x$是随机数，所以需要进行基于统计意义的均值计算：

KL散度就这么推导出来了。

参考：

张贤达《矩阵分析与应用》