曲线点抽稀算法-Python实现
何为抽稀
在处理矢量化数据时,记录中往往会有很多重复数据,对进一步数据处理带来诸多不便。多余的数据一方面浪费了较多的存储空间,另一方面造成所要表达的图形不光滑或不符合标准。因此要通过某种规则,在保证矢量曲线形状不变的情况下, 最大限度地减少数据点个数,这个过程称为抽稀。
通俗的讲就是对曲线进行采样简化,即在曲线上取有限个点,将其变为折线,并且能够在一定程度保持原有形状。比较常用的两种抽稀算法是:道格拉斯-普克(Douglas-Peuker)算法和垂距限值法。
道格拉斯-普克(Douglas-Peuker)算法
Douglas-Peuker算法(DP算法)过程如下:
- 1、连接曲线首尾两点A、B;
- 2、依次计算曲线上所有点到A、B两点所在曲线的距离;
- 3、计算最大距离D,如果D小于阈值threshold,则去掉曲线上出A、B外的所有点;如果D大于阈值threshold,则把曲线以最大距离分割成两段;
- 4、对所有曲线分段重复1-3步骤,知道所有D均小于阈值。即完成抽稀。
这种算法的抽稀精度与阈值有很大关系,阈值越大,简化程度越大,点减少的越多;反之简化程度越低,点保留的越多,形状也越趋于原曲线。
下面是Python代码实现:
# -*- coding: utf-8 -*-
"""
-------------------------------------------------
File Name: DouglasPeuker
Description : 道格拉斯-普克抽稀算法
Author : J_hao
date: 2017/8/16
-------------------------------------------------
Change Activity:
2017/8/16: 道格拉斯-普克抽稀算法
-------------------------------------------------
"""
from __future__ import division
from math import sqrt, pow
__author__ = 'J_hao'
THRESHOLD = 0.0001 # 阈值
def point2LineDistance(point_a, point_b, point_c):
"""
计算点a到点b c所在直线的距离
:param point_a:
:param point_b:
:param point_c:
:return:
"""
# 首先计算b c 所在直线的斜率和截距
if point_b[0] == point_c[0]:
return 9999999
slope = (point_b[1] - point_c[1]) / (point_b[0] - point_c[0])
intercept = point_b[1] - slope * point_b[0]
# 计算点a到b c所在直线的距离
distance = abs(slope * point_a[0] - point_a[1] + intercept) / sqrt(1 + pow(slope, 2))
return distance
class DouglasPeuker(object):
def __init__(self):
self.threshold = THRESHOLD
self.qualify_list = list()
self.disqualify_list = list()
def diluting(self, point_list):
"""
抽稀
:param point_list:二维点列表
:return:
"""
if len(point_list) < 3:
self.qualify_list.extend(point_list[::-1])
else:
# 找到与收尾两点连线距离最大的点
max_distance_index, max_distance = 0, 0
for index, point in enumerate(point_list):
if index in [0, len(point_list) - 1]:
continue
distance = point2LineDistance(point, point_list[0], point_list[-1])
if distance > max_distance:
max_distance_index = index
max_distance = distance
# 若最大距离小于阈值,则去掉所有中间点。 反之,则将曲线按最大距离点分割
if max_distance < self.threshold:
self.qualify_list.append(point_list[-1])
self.qualify_list.append(point_list[0])
else:
# 将曲线按最大距离的点分割成两段
sequence_a = point_list[:max_distance_index]
sequence_b = point_list[max_distance_index:]
for sequence in [sequence_a, sequence_b]:
if len(sequence) < 3 and sequence == sequence_b:
self.qualify_list.extend(sequence[::-1])
else:
self.disqualify_list.append(sequence)
def main(self, point_list):
self.diluting(point_list)
while len(self.disqualify_list) > 0:
self.diluting(self.disqualify_list.pop())
print self.qualify_list
print len(self.qualify_list)
if __name__ == '__main__':
d = DouglasPeuker()
d.main([[104.066228, 30.644527], [104.066279, 30.643528], [104.066296, 30.642528], [104.066314, 30.641529],
[104.066332, 30.640529], [104.066383, 30.639530], [104.066400, 30.638530], [104.066451, 30.637531],
[104.066468, 30.636532], [104.066518, 30.635533], [104.066535, 30.634533], [104.066586, 30.633534],
[104.066636, 30.632536], [104.066686, 30.631537], [104.066735, 30.630538], [104.066785, 30.629539],
[104.066802, 30.628539], [104.066820, 30.627540], [104.066871, 30.626541], [104.066888, 30.625541],
[104.066906, 30.624541], [104.066924, 30.623541], [104.066942, 30.622542], [104.066960, 30.621542],
[104.067011, 30.620543], [104.066122, 30.620086], [104.065124, 30.620021], [104.064124, 30.620022],
[104.063124, 30.619990], [104.062125, 30.619958], [104.061125, 30.619926], [104.060126, 30.619894],
[104.059126, 30.619895], [104.058127, 30.619928], [104.057518, 30.620722], [104.057625, 30.621716],
[104.057735, 30.622710], [104.057878, 30.623700], [104.057984, 30.624694], [104.058094, 30.625688],
[104.058204, 30.626682], [104.058315, 30.627676], [104.058425, 30.628670], [104.058502, 30.629667],
[104.058518, 30.630667], [104.058503, 30.631667], [104.058521, 30.632666], [104.057664, 30.633182],
[104.056664, 30.633174], [104.055664, 30.633166], [104.054672, 30.633289], [104.053758, 30.633694],
[104.052852, 30.634118], [104.052623, 30.635091], [104.053145, 30.635945], [104.053675, 30.636793],
[104.054200, 30.637643], [104.054756, 30.638475], [104.055295, 30.639317], [104.055843, 30.640153],
[104.056387, 30.640993], [104.056933, 30.641830], [104.057478, 30.642669], [104.058023, 30.643507],
[104.058595, 30.644327], [104.059152, 30.645158], [104.059663, 30.646018], [104.060171, 30.646879],
[104.061170, 30.646855], [104.062168, 30.646781], [104.063167, 30.646823], [104.064167, 30.646814],
[104.065163, 30.646725], [104.066157, 30.646618], [104.066231, 30.645620], [104.066247, 30.644621], ])
垂距限值法
垂距限值法其实和DP算法原理一样,但是垂距限值不是从整体角度考虑,而是依次扫描每一个点,检查是否符合要求。
算法过程如下:
- 1、以第二个点开始,计算第二个点到前一个点和后一个点所在直线的距离d;
- 2、如果d大于阈值,则保留第二个点,计算第三个点到第二个点和第四个点所在直线的距离d;若d小于阈值则舍弃第二个点,计算第三个点到第一个点和第四个点所在直线的距离d;
- 3、依次类推,直线曲线上倒数第二个点。
下面是Python代码实现:
# -*- coding: utf-8 -*-
"""
-------------------------------------------------
File Name: LimitVerticalDistance
Description : 垂距限值抽稀算法
Author : J_hao
date: 2017/8/17
-------------------------------------------------
Change Activity:
2017/8/17:
-------------------------------------------------
"""
from __future__ import division
from math import sqrt, pow
__author__ = 'J_hao'
THRESHOLD = 0.0001 # 阈值
def point2LineDistance(point_a, point_b, point_c):
"""
计算点a到点b c所在直线的距离
:param point_a:
:param point_b:
:param point_c:
:return:
"""
# 首先计算b c 所在直线的斜率和截距
if point_b[0] == point_c[0]:
return 9999999
slope = (point_b[1] - point_c[1]) / (point_b[0] - point_c[0])
intercept = point_b[1] - slope * point_b[0]
# 计算点a到b c所在直线的距离
distance = abs(slope * point_a[0] - point_a[1] + intercept) / sqrt(1 + pow(slope, 2))
return distance
class LimitVerticalDistance(object):
def __init__(self):
self.threshold = THRESHOLD
self.qualify_list = list()
def diluting(self, point_list):
"""
抽稀
:param point_list:二维点列表
:return:
"""
self.qualify_list.append(point_list[0])
check_index = 1
while check_index < len(point_list) - 1:
distance = point2LineDistance(point_list[check_index],
self.qualify_list[-1],
point_list[check_index + 1])
if distance < self.threshold:
check_index += 1
else:
self.qualify_list.append(point_list[check_index])
check_index += 1
return self.qualify_list
if __name__ == '__main__':
l = LimitVerticalDistance()
diluting = l.diluting([[104.066228, 30.644527], [104.066279, 30.643528], [104.066296, 30.642528], [104.066314, 30.641529],
[104.066332, 30.640529], [104.066383, 30.639530], [104.066400, 30.638530], [104.066451, 30.637531],
[104.066468, 30.636532], [104.066518, 30.635533], [104.066535, 30.634533], [104.066586, 30.633534],
[104.066636, 30.632536], [104.066686, 30.631537], [104.066735, 30.630538], [104.066785, 30.629539],
[104.066802, 30.628539], [104.066820, 30.627540], [104.066871, 30.626541], [104.066888, 30.625541],
[104.066906, 30.624541], [104.066924, 30.623541], [104.066942, 30.622542], [104.066960, 30.621542],
[104.067011, 30.620543], [104.066122, 30.620086], [104.065124, 30.620021], [104.064124, 30.620022],
[104.063124, 30.619990], [104.062125, 30.619958], [104.061125, 30.619926], [104.060126, 30.619894],
[104.059126, 30.619895], [104.058127, 30.619928], [104.057518, 30.620722], [104.057625, 30.621716],
[104.057735, 30.622710], [104.057878, 30.623700], [104.057984, 30.624694], [104.058094, 30.625688],
[104.058204, 30.626682], [104.058315, 30.627676], [104.058425, 30.628670], [104.058502, 30.629667],
[104.058518, 30.630667], [104.058503, 30.631667], [104.058521, 30.632666], [104.057664, 30.633182],
[104.056664, 30.633174], [104.055664, 30.633166], [104.054672, 30.633289], [104.053758, 30.633694],
[104.052852, 30.634118], [104.052623, 30.635091], [104.053145, 30.635945], [104.053675, 30.636793],
[104.054200, 30.637643], [104.054756, 30.638475], [104.055295, 30.639317], [104.055843, 30.640153],
[104.056387, 30.640993], [104.056933, 30.641830], [104.057478, 30.642669], [104.058023, 30.643507],
[104.058595, 30.644327], [104.059152, 30.645158], [104.059663, 30.646018], [104.060171, 30.646879],
[104.061170, 30.646855], [104.062168, 30.646781], [104.063167, 30.646823], [104.064167, 30.646814],
[104.065163, 30.646725], [104.066157, 30.646618], [104.066231, 30.645620], [104.066247, 30.644621], ])
print len(diluting)
print(diluting)
最后
其实DP算法和垂距限值法原理一样,DP算法是从整体上考虑一条完整的曲线,实现时较垂距限值法复杂,但垂距限值法可能会在某些情况下导致局部最优。另外在实际使用中发现采用点到另外两点所在直线距离的方法来判断偏离,在曲线弧度比较大的情况下比较准确。如果在曲线弧度比较小,弯曲程度不明显时,这种方法抽稀效果不是很理想,建议使用三点所围成的三角形面积作为判断标准。下面是抽稀效果:
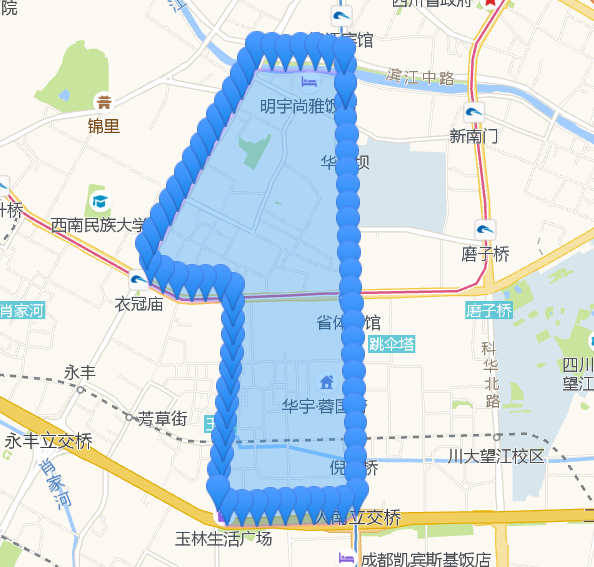
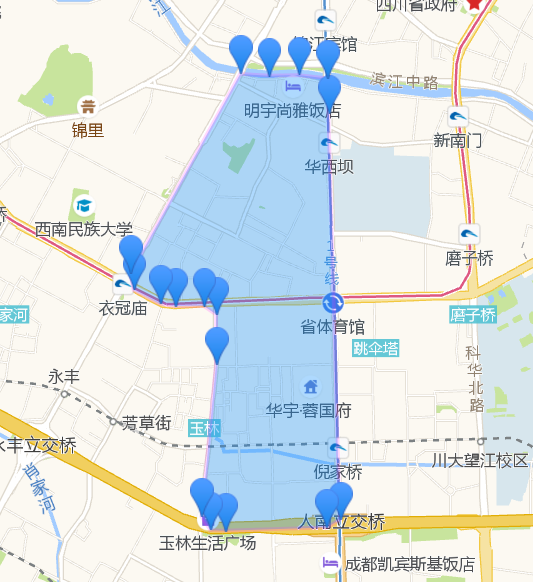
博文地址: http://www.spiderpy.cn/blog/detail/29
曲线点抽稀算法-Python实现的更多相关文章
- 模拟退火算法Python编程(2)约束条件的处理
1.最优化与线性规划 最优化问题的三要素是决策变量.目标函数和约束条件. 线性规划(Linear programming),是研究线性约束条件下线性目标函数的极值问题的优化方法,常用于解决利用现有的资 ...
- 模拟退火算法Python编程(3)整数规划问题
1.整数规划问题 整数规划问题在工业.经济.国防.医疗等各行各业应用十分广泛,是指规划中的变量(全部或部分)限制为整数,属于离散优化问题(Discrete Optimization). 线性规划问题的 ...
- pageRank算法 python实现
一.什么是pagerank PageRank的Page可是认为是网页,表示网页排名,也可以认为是Larry Page(google 产品经理),因为他是这个算法的发明者之一,还是google CEO( ...
- 常见排序算法-Python实现
常见排序算法-Python实现 python 排序 算法 1.二分法 python 32行 right = length- : ] ): test_list = [,,,,,, ...
- kmp算法python实现
kmp算法python实现 kmp算法 kmp算法用于字符串的模式匹配,也就是找到模式字符串在目标字符串的第一次出现的位置比如abababc那么bab在其位置1处,bc在其位置5处我们首先想到的最简单 ...
- KMP算法-Python版
KMP算法-Python版 传统法: 从左到右一个个匹配,如果这个过程中有某个字符不匹配,就跳回去,将模式串向右移动一位.这有什么难的? 我们可以 ...
- 压缩感知重构算法之IRLS算法python实现
压缩感知重构算法之OMP算法python实现 压缩感知重构算法之CoSaMP算法python实现 压缩感知重构算法之SP算法python实现 压缩感知重构算法之IHT算法python实现 压缩感知重构 ...
- 压缩感知重构算法之OLS算法python实现
压缩感知重构算法之OMP算法python实现 压缩感知重构算法之CoSaMP算法python实现 压缩感知重构算法之SP算法python实现 压缩感知重构算法之IHT算法python实现 压缩感知重构 ...
- 压缩感知重构算法之CoSaMP算法python实现
压缩感知重构算法之OMP算法python实现 压缩感知重构算法之CoSaMP算法python实现 压缩感知重构算法之SP算法python实现 压缩感知重构算法之IHT算法python实现 压缩感知重构 ...
随机推荐
- JavaScript学习笔记(二)——选项卡小结
Js制作选项卡小结 1.先构思好需要展示的页面效果,比如这样 2.需要显示的效果通过html和css制作出来,包括选项(第一课.第二课)的鼠标停留背景变色.下方选项页内容切换的内容等. 3.把此选项卡 ...
- HTTP通过请求和响应的交换达成通信
1. 通过请求和响应的交换达成通信 首先我们来看一个HTTP请求报文: GET/index.htm HTTP/1.1 HOST : hacker.jp HTTP协议起始行开头的GET表示请求访问服务器 ...
- Java jvm级别native关键词、JNI详解
1.native关键词的引入 再完美的编程语言也有自己的不足之处,当然Java也不例外,Java的不足之处除了体现在运行速度(这点往往被一些其他编程语言使用者所诟病)上要比传统的C++慢许多之外,Ja ...
- JAVA - 深入JAVA 虚拟机 1
Java虚拟机与程序的生命周期 Java虚拟机将结束生命周期 1.call System.exit(n) Terminates the currently running JVM. 2.程序正常执行结 ...
- python编程快速上手之第5章实践项目参考答案
#!/usr/bin/env python3.5 # coding:utf-8 # 5.6.1 # 好玩游戏的物品清单 # 给定一个字典,包含物品名称和数量,并打印出数量对应的物品 dict_stuf ...
- Centos7yum安装Redis详细教程
原本是在自己的mac上安装redis的,通过brew去安装的redis觉得很简单,实际macos系统与centos系统还是有一些区别的. 1.yum安装redis服务 sudo yum install ...
- editPuls 常用知识
1.创建模板 1).创建模板页(*.html) 2).Tools->Preferences->File->Templates->HTML->file name重新选定模板 ...
- 关于MySQL的commit非规律性失败案例的深入分析
案例描述: 一个普通的事务提交,在应用里面会提示commit超时,失败. 一.理论知识 1.关于commit原理,事务提交过程 1.寻找修改的数据页: 1.如果该数据页在内存中,则直接是内存读: 2. ...
- Luogu 1402 酒店之王(二分图最大匹配)
Luogu 1402 酒店之王(二分图最大匹配) Description XX酒店的老板想成为酒店之王,本着这种希望,第一步要将酒店变得人性化.由于很多来住店的旅客有自己喜好的房间色调.阳光等,也有自 ...
- Xamarin Android绑定微信SDK
现在几乎所有的APP都集成了向微博,微信等社交平台分享的功能.这些社交平台官方也提供了SDK让开发者使用,对于Android和IOS平台而言,只需要下载官方的SDK,按照官方说明文档进行集成就可以轻松 ...
