【字符串算法2】浅谈Manacher算法

【字符串算法1】 字符串Hash（优雅的暴力）

【字符串算法2】Manacher算法

【字符串算法3】KMP算法

这里将讲述  字符串算法2：Manacher算法

问题：给出字符串S(限制见后)求出最大回文子串长度

Subtask1  对于10%的数据 |S|∈(0,100]

Subtask2  对于30%的数据|S|∈(0,5000]

Subtask3 对于100%的数据|S|∈(0,11000000]

Subtask1（10pts）：最朴素的暴力 枚举字符串的所有子串，判断其是否回文，时间复杂度是O(n³)的

Subtask2（30pts）：利用回文串的性质：  所有的回文串都是对称的。

长度为奇数回文串以最中间字符的位置为对称轴左右对称，

而长度为偶数的回文串的对称轴在中间两个字符之间的空隙。

可以遍历这些对称轴，

在每个对称轴上同时向左和向右扩展，直到左右两边的字符不同或者到达边界。

时间复杂度O（n²）

Subtask3（100pts）：？（当然是Manacher算法囖）O（n）

改进优化 Subtask2（30pts） ：

1.麻烦程度（预处理字符串）

在每两个字符中间插入另一个字符，如'#'。

也就是说，原来的字符串是这样的

现在的字符串是这样的（为了不越界以及方便，a[0]设置为‘#’）

那么这个缺点解决了（现在不用分奇数偶数讨论了qwq）

【图是哪里偷过来的，足以说明问题】

2.会出现很多子串被重复多次访问，时间效率大幅降低。

要想降维 O(n)的做法是每一位只扫一次或常数次这里每一位都扫了将近n次

------------------（正文分割线）----------------------

定义几个变量P[i]表示在处理过后的数组中的第i个点最长向左边拓展P[i]个数位都能保证他是回文（右边不记录因为左右对称）

那么p[1]=1,p[2]=2,p[3]=1,p[4]=2,p[5]=1,p[6]=2,p[7]=5,p[8]=2,p[9]=1,p[10]=2,p[11]=1,p[12]=2,p[13]=1;

可以发现所有#的地方大部分都是1

其实上面那句话是错的！！！  p[7]=5 ???

重点来了：

P[i]-1代表什么？ 原串（不插入#前）中第i位置的回文串长度（包含中间点）

证明：

1、显然L=2*P[i]-1即为新串（加#）中以第i个点为中心最长回文串长度。
2、以第i位 为中心的回文串一定是以#开头和#结尾的，例如“#b#b#”或“#b#a#b#”
所以L减去最前或者最后的‘#’字符就是原串中长度的二倍，即原串长度为(L-1)/2，化简的P[i]-1。

得证。

【再偷2张图片】

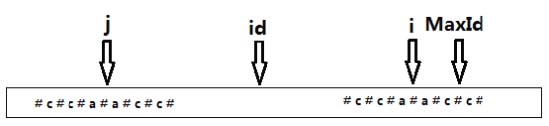
maxId表示前面运行过程中求得最大回文串的最右端

id（后面程序是MID）表示此时最大回文串的对称点，i代表当前遍历到第i个位置

显然我们可以轻易算出i关于id（MID）对称点的坐标j

由id是ij的中点可知 (i+j)/2=id，由此可知 j=2*id-i（所以程序运行的时候就不用记录j了直接用id和i算就行）

运用动态规划的思想在算P[i]的时候P[j] | j∈ [1,i) 都已经算出那么若j为i关于id（MID）的对称点那么P[i]∈ [P[j],+∞)

就是P[i]不可能比P[j]短，为什么呢？

利用回文串的对称性j和i关于id（MID）对称，MaxId和左边MinId（对于id（MID）的对称点）关于id对称

那么j到id回文串半径为P[j]，对称过来到id右边i的左边那么回文串半径也为P[j]，

而P[i]没有算出来所以就是P[i]不可能比P[j]短 即 P[i]∈ [P[j],+∞)

分类讨论：

若对称过来超过MaxId那么这样的对称是不合法的 P[j]=1从该点老老实实向两边拓展

就是P[j]对称到i的左右，i右端超过MaxId（触及不该触及的地方），就是不合法，因为右边你并不知道

若对称过来没有超过MaxId那么这样的对称是合法的 P[i]=p[j]然后往右拓展

在移动的过程中顺便更新MaxId和P[i]就行

到这里你已经完成了 Subtask3 对于100%的数据|S|<10000000的数据

复杂度证明？

manacher算法只需要线性扫描一遍预处理后的字符串。
对p[]数组的处理 i 为 j 关于 id 的对称点

1. (i<MaxId)

• Maxid-i>p[j] p[j]=p[i]
• 其他情况 p[i]=MaxId-i

2.其他情况 p[i]=0

1. 在i<MaxId的情况下，p的值可以在O(1) 时间内确定
2. 在i>MaxId 的情况下，p的值需要O(n) 的时间内确定，

但是在情况2下，每次扫描都从MaxId开始，且MaxId自身的变化情况是单调递增的，

这样可以保证，字符串中的每个字符最多被访问2次，

所以，该算法的时间复杂度是线性O(n)

只需要弄清楚两点:

1.while()循环本身的时间复杂度在没有前提条件的情况下确实是O(n)

2.但是这里的MaxId，是不断往后走而不可能往前退的，它自身的值的变化是递增的。

那么你可以明白，要进入while循环，

i 的值必然是比MaxId大的，

也就是说整个程序结束为止，

while循环执行的操作数为n次（线性次），

而字符串中的每个字符，最多能被访问到2次。

时间复杂度必然为O(n)

贴下代码：

# include <bits/stdc++.h>
using namespace std;
const int MAXN=*;
char a[*MAXN];
int p[*MAXN];
int main()
{
    char ch=getchar();int t=; a[]='?';//为了保险起见a[0]和最后的符号不能一样
    while (isalpha(ch)) {
        t++;
        a[*t]=ch; a[*t-]='#';
        ch=getchar();
    }
    a[*t+]='#';
    int n=*t+;
    int MID=,R=,i; //MID就是id，R就是MaxId，i就是i
    for (i=;i<=n;i++) {
        if (R>i) p[i]=min(p[*MID-i],R-i);
        else p[i]=;
        while (a[i-p[i]]==a[i+p[i]]) p[i]++;
        if (i+p[i]>R) R=i+p[i],MID=i;
    }
    int ans=;
    for (int i=;i<=n;i++) ans=max(ans,p[i]-);
    printf("%d\n",ans);
    return ;
}

这是一道真正的模板题qwq:

P3805 【模板】manacher算法

题目描述

给出一个只由小写英文字符a,b,c...y,z组成的字符串S,求S中最长回文串的长度.

字符串长度为n

输入输出格式

输入格式：

一行小写英文字符a,b,c...y,z组成的字符串S

输出格式：

一个整数表示答案

输入输出样例

输入样例#1：

aaa

输出样例#1：

3

说明

字符串长度|S| <= 11000000

 这里有着注意点：不能判断回车否则是TLE，应该判断不是字母时果断跳出