【Java】 大话数据结构(9) 树（二叉树、线索二叉树）

本文根据《大话数据结构》一书，对Java版的二叉树、线索二叉树进行了一定程度的实现。

另：

二叉排序树（二叉搜索树）

平衡二叉树(AVL树)

二叉树的性质

性质1：二叉树第i层上的结点数目最多为 2^{i-1} (i≥1)。

性质2：深度为k的二叉树至多有2^{k}-1个结点(k≥1)。

性质3：在任意一棵二叉树中，若终端结点的个数为n₀，度为2的结点数为n₂，则n₀=n₂+1。

　　　　证明提示：分支线总数=n₀+n₁+n₂-1=n₁+2×n₂

性质4：具有n个节点的完全二叉树的深度为[log₂n]+1。（[ ]代表向下取整）

　　　　证明提示：假设深度为k，则有2^{k-1} -1＜n≤2^{k} -1。

性质5：如果有一颗有n个节点的完全二叉树的节点按层次序编号，对任一层的节点i（1<=i<=n）有

1.如果i=1，则节点是二叉树的根，无双亲，如果i>1，则其双亲节点为[i/2]

2.如果2i>n那么节点i没有左孩子（叶子结点），否则其左孩子为2i

3.如果2i+1>n那么节点没有右孩子，否则右孩子为2i+1

二叉链表的定义代码

class BiTNode<E>{
	E data;
	BiTNode<E> lchild,rchild;
	public BiTNode(E data) {
		this.data=data;
		this.lchild=null;
		this.rchild=null;
	}
}

public class BiTree<E> {

	private BiTNode<E> root;

	public BiTree() {
		root=null;
	}

        ...
}

　　

　　

二叉树的遍历

	/*
	 * 前序遍历
	 */
	public void preOrder() {
		preOrderTraverse(root);
		System.out.println();
	}
	private void preOrderTraverse(BiTNode<E> node) {
		if(node==null)
			return;
		System.out.print(node.data);
		preOrderTraverse(node.lchild);
		preOrderTraverse(node.rchild);
	}

	/*
	 * 中序遍历
	 */
	public void inOrder() {
		inOrderTraverse(root);
		System.out.println();
	}
	private void inOrderTraverse(BiTNode<E> node) {
		if(node==null)
			return;
		inOrderTraverse(node.lchild);
		System.out.print(node.data);
		inOrderTraverse(node.rchild);
	}

	/*
	 * 后序遍历
	 */
	public void postOrder() {
		postOrderTraverse(root);
		System.out.println();
	}
	private void postOrderTraverse(BiTNode<E> node) {
		if(node==null)
			return;
		postOrderTraverse(node.lchild);
		postOrderTraverse(node.rchild);
		System.out.print(node.data);
	}

　　

二叉树的建立

　　《大话》一书中，6.9节关于二叉树的建立如下：

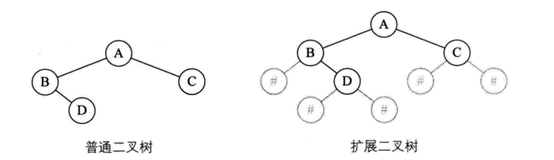
　　通过输入AB#D##C##，可以生成上述二叉树，其C语言的实现算法如下：

　　暂时能力有限，还不懂如何改为Java代码。

　　几点疑问：1.exit(OVERFLOW)不是很清楚什么意思；

　　　　　　　2.代码中为char类型，如何用于泛型？

　　　　　　   3.scanf()在Java中怎么实现？用scanner吗？程序如何知道输入完“AB#D##C##”就结束二叉树的构造呢？总的实现代码（包括main部分）是怎么样的？

以下为测试代码遍历的总体测试代码：

package BiTree;

class BiTNode<E>{
	E data;
	BiTNode<E> lchild,rchild;
	public BiTNode(E data) {
		this.data=data;
		this.lchild=null;
		this.rchild=null;
	}
}

public class BiTree<E> {

	private BiTNode<E> root;

	public BiTree() {
		//root=new BiTNode(null, null, null);
		root=null;
	}

	/*
	 * 前序遍历
	 */
	public void preOrder() {
		preOrderTraverse(root);
		System.out.println();
	}
	private void preOrderTraverse(BiTNode<E> node) {
		if(node==null)
			return;
		System.out.print(node.data);
		preOrderTraverse(node.lchild);
		preOrderTraverse(node.rchild);
	}

	/*
	 * 中序遍历
	 */
	public void inOrder() {
		inOrderTraverse(root);
		System.out.println();
	}
	private void inOrderTraverse(BiTNode<E> node) {
		if(node==null)
			return;
		inOrderTraverse(node.lchild);
		System.out.print(node.data);
		inOrderTraverse(node.rchild);
	}

	/*
	 * 后序遍历
	 */
	public void postOrder() {
		postOrderTraverse(root);
		System.out.println();
	}
	private void postOrderTraverse(BiTNode<E> node) {
		if(node==null)
			return;
		postOrderTraverse(node.lchild);
		postOrderTraverse(node.rchild);
		System.out.print(node.data);
	}

	/*
	 * 6.9 二叉树的建立暂时不会,略
	 */

	public static void main(String[] args) {
		BiTree<String> aBiTree = new BiTree<String>();
		aBiTree.root=new BiTNode("A");
		aBiTree.root.lchild=new BiTNode("B");
		aBiTree.root.rchild=new BiTNode("C");
		aBiTree.root.lchild.rchild=new BiTNode("D");
		System.out.println("————前序————");
		aBiTree.preOrder();
		System.out.println("————中序————");
		aBiTree.inOrder();
		System.out.println("————后序————");
		aBiTree.postOrder();
	}
}

　　

————前序————
ABDC
————中序————
BDAC
————后序————
DBCA

BiTree

线索二叉树

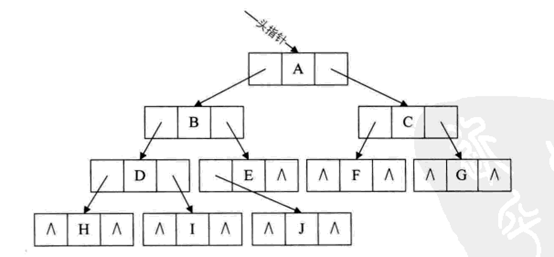
　　对一个有n个节点的二叉链表（如上图），整表存在2n个指针域，但分支线只有n-1条，说明空指针域的个数为2n-(n-1) = n+1个，浪费了很多的内存资源。

　　我们可以通过利用这些空指针域，存放节点在某种遍历方式下的前驱和后继节点的指针。我们把这种指向前驱和后继的指针成为线索，加上线索的二叉链表成为线索链表，对应的二叉树就成为“线索二叉树(Threaded Binary Tree)”，如下图所示。

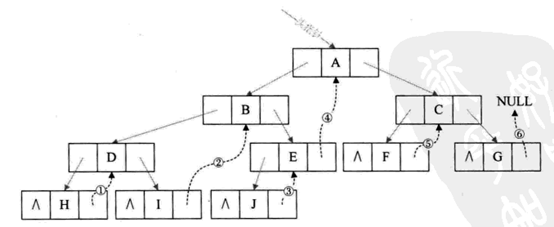
　　线索二叉树的Java代码如下：

package BiThrTree;

/**
 * 线索二叉树
 * 包含二叉树的中序线索化及其遍历
 * @author Yongh
 *
 */
class BiThrNode<E>{
	E data;
	BiThrNode<E> lChild,rChild;
	boolean lTag,rTag;
	public BiThrNode(E data) {
		this.data=data;
		//tag都先定义成左右孩子指针。
		lTag=false;  //其实把Tag定义为IsThread更好
		rTag=false;
		lChild=null;
		rChild=null;
	}
}

public class BiThrTree<T> {
	BiThrNode<T> root;
	boolean link=false,thread=true;

	public BiThrTree() {
		root=null;
	}

	/*
	 * 中序线索化二叉树
	 * 即：在遍历的时候找到空指针进行修改。
	 */
	BiThrNode<T> pre;	//线索化时记录的前一个结点

	public void inThreading() {
		inThreading(root);
	}
	private void inThreading(BiThrNode<T> p) {
		if(p != null) {
			inThreading(p.lChild);
			if(p.lChild==null) {
				p.lTag=thread;
				p.lChild=pre;
			}
			if(pre!=null && pre.rChild==null) {  //pre!=null一定要加上
				pre.rTag=thread;
				pre.rChild=p;
			}
			pre=p;                               //别忘了在这个位置加上pre=p
			inThreading(p.rChild);
		}
	}

	/*
	 * 中序遍历二叉线索链表表示的二叉树(按后继方式)
	 * 书中添加了一个头结点，本程序中不含头结点
	 * 思路：先找到最左子结点
	 */
	public void inOrderTraverse() {
		BiThrNode<T> p = root;
		while(p!=null) {
			while(p.lTag==link)
				p=p.lChild;    //找到最左子结点
			System.out.print(p.data);
			while(p.rTag==thread) {   //不是if
				p=p.rChild;
				System.out.print(p.data);
			}
			p=p.rChild;
		}
		System.out.println();
	}

	/*
	 * 中序遍历方法二(按后继方式)
	 * 参考别人的博客
	 */
	public void inOrderTraverse2() {
		BiThrNode<T> node = root;
        while(node != null && node.lTag==link) {
            node = node.lChild;
        }
        while(node != null) {
            System.out.print(node.data + ", ");
            if(node.rTag==thread) {//如果右指针是线索
                node = node.rChild;

            } else {    //如果右指针不是线索，找到右子树开始的节点
                node = node.rChild;
                while(node != null && node.lTag==link) {
                    node = node.lChild;
                }
            }
        }
        System.out.println();
	}

	public static void main(String[] args) {
		BiThrTree<String> aBiThrTree = new BiThrTree<String>();
		aBiThrTree.root=new BiThrNode<String>("A");					//		A
		aBiThrTree.root.lChild=new BiThrNode<String>("B");			//    /   \
		aBiThrTree.root.lChild.lChild=new BiThrNode<String>("C");	    //	 B     D
		aBiThrTree.root.rChild=new BiThrNode<String>("D");			//  /     / \
		aBiThrTree.root.rChild.lChild=new BiThrNode<String>("E");     // C     E   F
		aBiThrTree.root.rChild.rChild=new BiThrNode<String>("F");
		aBiThrTree.inThreading();
		aBiThrTree.inOrderTraverse();
		aBiThrTree.inOrderTraverse2();
	}
}　

　　

CBAEDF
C, B, A, E, D, F, 

BiThrTree

推荐阅读：

　　线索二叉树原理及前序、中序线索化（Java版）（文中对线索二叉树的介绍和代码都比较清晰，且更加全面）。

赫夫曼树及其应用

　　带权路径长度WPL最小的二叉树称为最优二叉树，也称为赫夫曼树(Huffman Tree)。

　　赫夫曼编码：

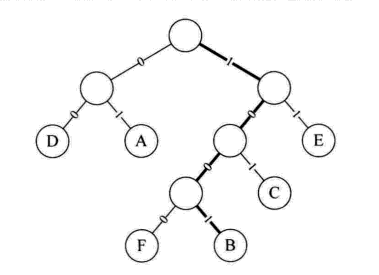
　　推荐阅读：哈夫曼树(三)之 Java详解