经典排序算法 — C#版本（中）

归并排序比较适合大规模得数据排序，借鉴了分治思想。

归并排序原理

自古以来，分久必合合久必分。

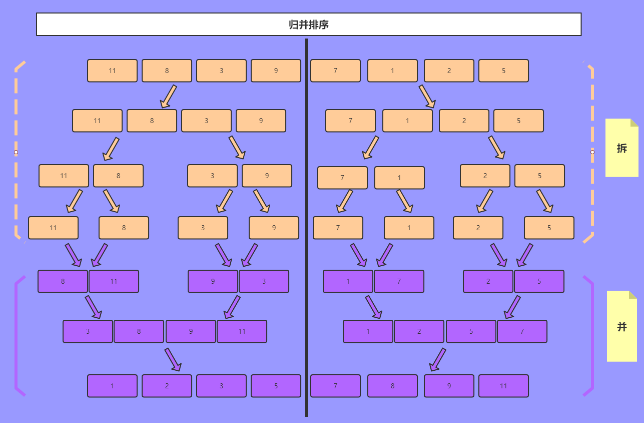
我们可以这样理解归并排序，分-分到不能分为止，然后合并。

使用递归将问题一点一点分解，最后进行合并。

分而治之 （merge_sort）

提到递推，我们使用地递推解决问题，首先要分析出递推公式、明确结束条件。

递推公式：

merge_sort(i...n)=merge( merge_sort(i...j), merge_sort(j+...n) )

结束条件：
i>=n

分久必合（merge）

将两个有序的数组进行合并，这样整个数组也就是排序好的数组了。

那么怎么进行合并呢？-- (i...j) 和 (j+1...n) 重新排序后，重新放入原来的数组 (i...n)

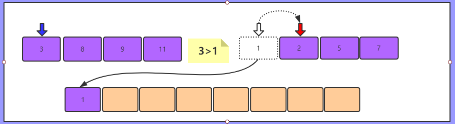
两组数组 [3, 8, 9, 11]   vs  [1, 2, 5, 7]

两个游标      蓝色         和       红色

 3>1，1小，1入新数组，红色游标后移一位，继续比较...

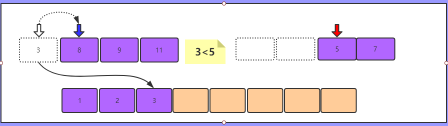
  3>2，2小，2入数组，红色游标后移一位

  3<5，3小，3入数组，蓝色游标后移一位

8>5，5小，5入数组，红色游标后移一位

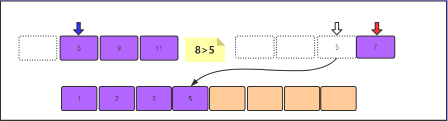
8>7，7小，7入数组，红色游标后移，右侧数组全部转移完毕

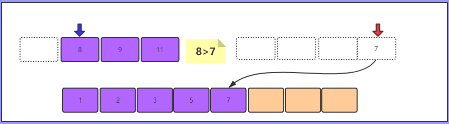
当有一组数组全部转移完毕，那么剩下的一组中的全部元素依次转入到新数组中，新数组正式成为一个有顺序的数组

通过以上两点：递推公式和合并思想，我们使用代码实现一下：

1、如下图：递归方式 进行分解，然后使用合并代码进行合并。

          /// <summary>
         /// 递归调用
         /// </summary>
         /// <param name="a">原始数组</param>
         /// <param name="p">分割点</param>
         /// <param name="r">结束位置</param>
         public static void MergrSortInternally(int[] a, int p, int r)
         {
             //结束条件
             if (p >= r)
                 return;

             //切割点
             int q = p + (r - p) / ;

             //分而治之
             MergrSortInternally(a, p, q);

             MergrSortInternally(a, q + , r);

             //合并  A(a, p, q) 和  A(a, q + 1, r)
             Merage(a, p, q, r);

         }

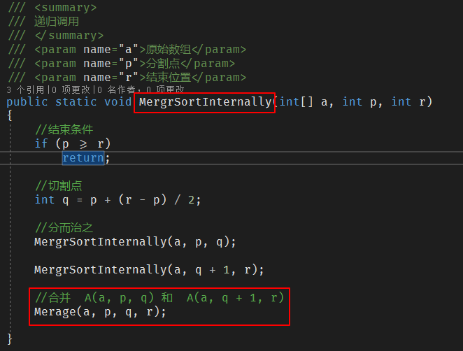
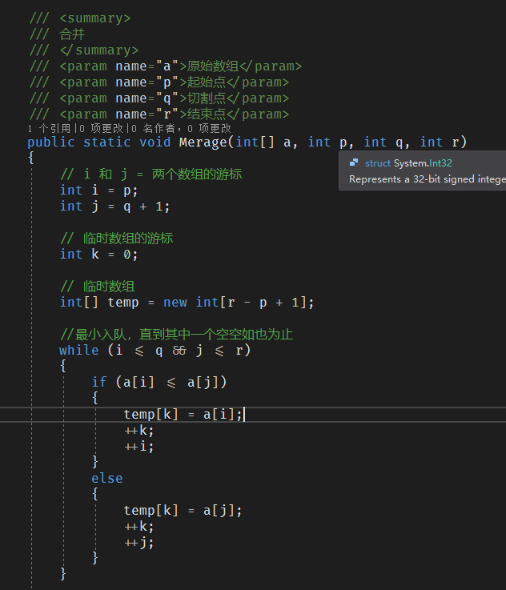
2、我们再来看看合并逻辑

参数：原始数组，开始的地方，切割的地方，结束的地方

逻辑：两个切割数组的各自的游标

申请同样大小的临时数组

　　　　 循环比较；小的入临时，游标后移；知道有一个数组空了为止

找到剩下不为空的那个数组，将剩余元素入临时

将临时数组，找到原始数组的对应为止进行覆盖

 /// <summary>
         /// 合并
         /// </summary>
         /// <param name="a">原始数组</param>
         /// <param name="p">起始点</param>
         /// <param name="q">切割点</param>
         /// <param name="r">结束点</param>
         public static void Merage(int[] a, int p, int q, int r)
         {
             // i 和 j = 两个数组的游标
             int i = p;
             int j = q + ;

             // 临时数组的游标
             int k = ;

             // 临时数组
             int[] temp = new int[r - p + ];

             //最小入队，直到其中一个空空如也为止
             while (i <= q && j <= r)
             {
                 if (a[i] <= a[j])
                 {
                     temp[k] = a[i];
                     ++k;
                     ++i;
                 }
                 else
                 {
                     temp[k] = a[j];
                     ++k;
                     ++j;
                 }
             }

             // 找到另一个不为空的，找到剩下的元素
             int start = i;
             int end = q;

             if (j <= r)
             {
                 start = j;
                 end = r;
             }

             // 剩余数组拷贝到临时数组 temp
             while (start <= end)
             {
                 temp[k++] = a[start++];
             }

             // 将temp覆盖到a[p...r]
             for (i = ; i <= r - p; ++i)
             {
                 a[p + i] = temp[i];
             }
         }

归并排序性能分析

 Q：是不是稳定排序？

 A：是

对于这两组数组   A[p...q] 和   A[q+1...r] 来说

代码中也是这样实现的，a[i]就是左侧数组，a[j]就是右侧数组，保证相等时左侧优先入队即可。注意 等号位置。

　

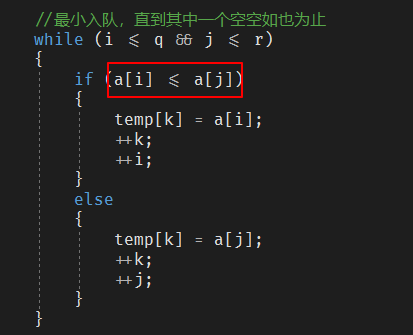
Q：是否是原地排序？

 A：当然不是

因为我们在合并代码时候，申请了同样大小的内存空间。

但是对于这里的归并排序的空间复杂度又是多少呢？

虽然牵扯到了递归，但是临时变量这里会在一个函数结束后栈会释放，所以空间复杂度是O(n)

Q：时间复杂度又是多少呢？

 A：O(n log n)

我们对 n 个元素的归并排序时间记作 T(n)，

分解函数分解两个子数组的时间是T(n/2)

合并函数时间复杂度是O(n)

T（1）=C;    n=1

T（n）=2*T（n/2）+ n; n>1

T(n)  =  2*T(n/2)  +  n
         = 2*(2*T(n/4) + n/2) + n = 4*T(n/4) + 2*n
         = 4*(2*T(n/8) + n/4) + 2*n = 8*T(n/8) + 3*n
         = 8*(2*T(n/16) + n/8) + 3*n = 16*T(n/16) + 4*n
　　  ......
　　  = 2^k * T(n/2^k) + k * n

T(n)  = 2^k * T(n/2^k) + k * n

当 T(n/2^k) = T（1）=> k = log2 n

即：T(n) = Cn + n log2 n  => O(n log n)