A direct formulation for sparse PCA using semidefinite programming

目录

• 背景
• Sparse eigenvectors(单个向量的稀疏化)
  • 初始问题（low-rank的思想？）
  • 等价问题
  • 最小化\(\lambda\) 得到下列问题（易推）
  • 再来一个等价问题
  • 条件放松（凸化）
• A robustness interpretation
• 收缩
• 关于半正定规划，回头再看看。

背景

上篇总结了一些收缩法，这篇论文就是一个示例，虽然这篇论文是在那人之前写的。

Sparse eigenvectors(单个向量的稀疏化)

\(A \in \mathrm{S}^{n} \rightarrow n\times n半正定矩阵\)

初始问题（low-rank的思想？）

\(\mathbf{Card}(x)\)表示\(x\)里面的非零元的个数。

等价问题

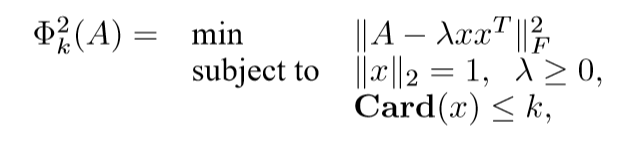
最小化\(\lambda\) 得到下列问题（易推）

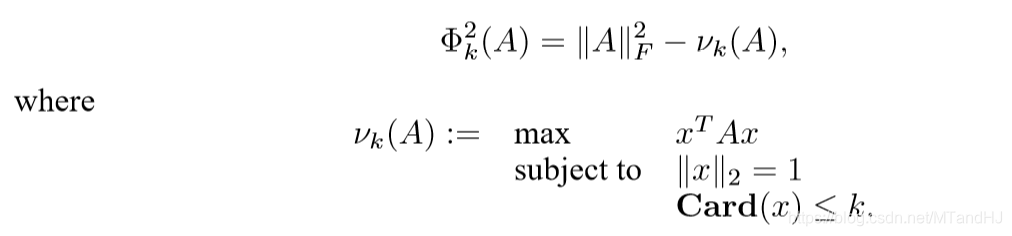
再来一个等价问题

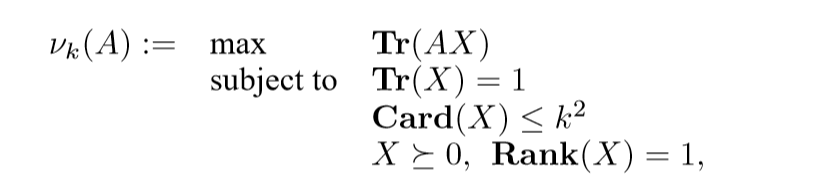
思路：
\(x^\mathrm{T}Ax=\mathbf{Tr}(x^\mathrm{T}Ax) = \mathbf{Tr}(Axx^{\mathrm{T}})\)
\(xx^{\mathrm{T}}\rightarrow X\)
显然\(X\)是需要符合那些额外条件的。

条件放松（凸化）

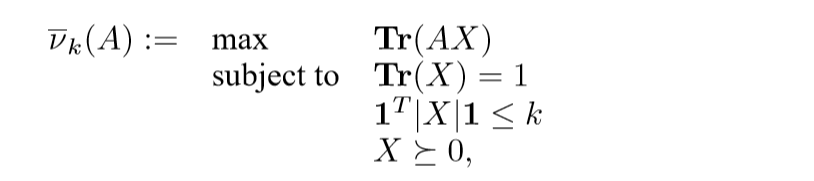
A robustness interpretation

考虑惩罚项：

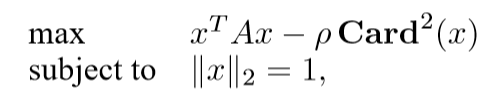
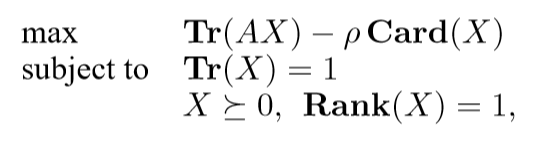
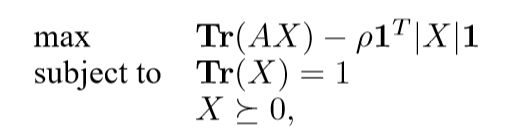
最大化最小，体现了robust？

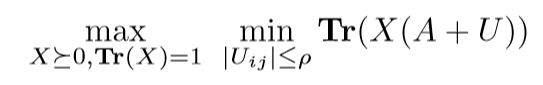
最后是算了最大里面的最小，这才是robust?

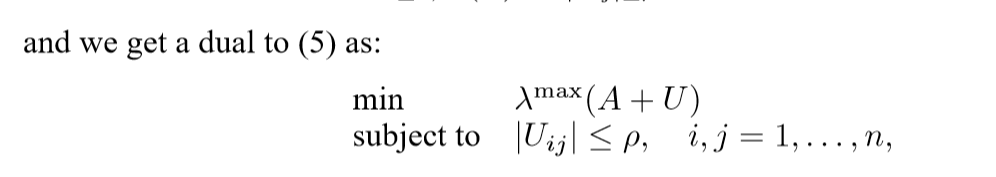
收缩

结果就是取\(X\)的首特征向量，然后，再利用Hotelling's deflation（之前也分析过了，这个收缩方法其实并不适用，用正交投影比较好）。

关于半正定规划，回头再看看。