【清北学堂2018-刷题冲刺】Contest 4

Task 1：序列

【问题描述】

 小H原本有一个由连续的正整数组成的序列，如{4,5,6}或{10,11,12,13,14,15,16}，但是她最近睡眠不足，只能记得其中的一些数字。她想知道，她最少可能只忘了多少数字。

【输入】

 第一行一个整数N表示小H记得的数的个数。

 第二行N个正整数Ai表示小H记得的数，保证Ai互不相同但是以打乱的顺序给出。

【输出】

 一行一个整数表示答案。

【输入输出样例】

4 10 13 12 8 

2

【样例解释】

 可能的原序列是{8,9,10,11,12,13}，小H只忘记了{9,11}两个数。

【数据范围】

• 1 – 4 1 ≤ N，Ai ≤ 100

• 5 – 8 1 ≤ N，Ai ≤ 1000

• 9 - 10 1 ≤ N ≤ 106,1 ≤ Ai ≤10^9

傻X题，直接水过。数据范围的话，N的范围实际上有点危险，建议手写max，min+快读。

#include<cstdio>
inline int max(int x,int y){return x>y?x:y;}
inline int min(int x,int y){return x<y?x:y;}
inline int read(){
	int s=0;
	char ch=getchar();
	while('9'<ch||ch<'0'){
		ch=getchar();
	}
	while('0'<=ch&&ch<='9'){
		s=s*10+ch-'0';
		ch=getchar();
	}
	return s;
}
int main(){
	freopen("sequence.in","r",stdin);
	freopen("sequence.out","w",stdout);
	int maxn=0,minn=0x3f3f3f3f,n=read();
	register int tmp;
	for(register int i=1;i<=n;++i){
		tmp=read();
		maxn=max(maxn,tmp);
		minn=min(minn,tmp);
	}
	printf("%d\n",maxn-minn-n+1);
	return 0;
}

---

Task 2：食物

【问题描述】

 小H喜欢吃肉、鱼和巧克力，但她不喜欢某些食用的顺序。

 小H每小时都会吃肉、鱼和巧克力其中一种。但如果出现以下情况，她就会不开心：

• 有连续3小时吃同一种食物。

• 有连续3小时她吃了所有种类的食物且中间那小时吃的是巧克力。

• 有连续3小时她在中间那小时吃了肉或鱼而此外的两小时吃的是巧克力。

 小H想知道，有多少种吃东西的序列能让自己在连续N个小时保持开心。

 你只需要输出答案对1000000007取模后的值。

【输入】

 第一行一个整数T表示数据组数。

 接下来T行每行一个整数N。

【输出】

 对于每组数据输出一行一个整数表示答案。

【输入输出样例】

3 3 4 15 

20 46 435170

【数据范围】

• 1 – 6 1 ≤ N ≤ 10^6
• 7 – 10 1 ≤ N ≤ 10^9

 对于这个题目来说，搜索很显然是不可能跑得动的。

 先考虑最直观的想法：直接DP，进行转移。复杂度O(nT)。

 设三种食物分别为1，2，3，那么有几种情况是不可用的：

• 1 1 1

• 2 2 2

• 3 3 3

• 1 3 2

• 2 3 1

• 3 1 3

• 3 2 3

 

 排除这些情况，其他的直接进行转移即可。

 但是很显然1e9的总复杂度再带上一个不小的常数是不可能跑过去的，60pts都没有。这是我们会发现：输入只有一个变量，而询问有1000次。我们考虑O(n)预处理优化一下，提前存储答案，就有了60pts。

 100pts的写法呢？看到1e9的数据就应该意识到这是一个矩阵加速递推的题目

 首先我们把3x3的状态压缩成1x9来看看最初的转移：

 我们的转移就这样变成了可以被矩阵优化的形式，接下来的操作就变得自然而然：构造一个9x9的矩阵。

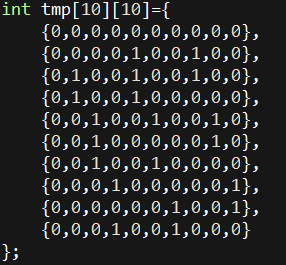
 经过大力构造，我们就得到了这样一个东西：

 按照我们构造时候的定义，答案矩阵就是初始矩阵*tmp^(n-2)了，矩阵快速幂大力跑过去，100pts到手。

#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
const int mod=1000000007;
int tmp[10][10]={
	{0,0,0,0,0,0,0,0,0,0},
	{0,0,0,0,1,0,0,1,0,0},
	{0,1,0,0,1,0,0,1,0,0},
	{0,1,0,0,1,0,0,0,0,0},
	{0,0,1,0,0,1,0,0,1,0},
	{0,0,1,0,0,0,0,0,1,0},
	{0,0,1,0,0,1,0,0,0,0},
	{0,0,0,1,0,0,0,0,0,1},
	{0,0,0,0,0,0,1,0,0,1},
	{0,0,0,1,0,0,1,0,0,0}
};
int bg[2][10]={
	{0,0,0,0,0,0,0,0,0,0},
	{0,1,1,1,1,1,1,1,1,1}
};//state of begin 

struct Matrix{
	int mp[10][10];
	void Init(){
		memset(mp,0,sizeof(mp));
	}
	void Unit(){
		memset(mp,0,sizeof(mp));
		for(int i=1;i<=9;++i){
			mp[i][i]=1;
		}
	}
};
Matrix __mul(Matrix x,Matrix y){
	Matrix ans;
	ans.Init();
	for(register int i=1;i<=9;++i){
		for(register int j=1;j<=9;++j){
			for(register int k=1;k<=9;++k){
				ans.mp[i][k]=(ans.mp[i][k]+(long long)x.mp[i][j]*y.mp[j][k])%mod;
			}
		}
	}
	return ans;
}
Matrix __pow(Matrix tmp,int p){
	Matrix ans;
	ans.Unit();//initialize
	while(p){
		if(p&1){
			p^=1;
			ans=__mul(ans,tmp);
		}
		p>>=1;
		tmp=__mul(tmp,tmp);
	}
	return ans;

}
int main(){
	freopen("food.in","r",stdin);
	freopen("food.out","w",stdout);
	Matrix mat;
	for(int i=0;i<=9;++i){
		for(int j=0;j<=9;++j){
			mat.mp[i][j]=tmp[i][j];
		}
	}
	int T,n;
	scanf("%d",&T);
	while(T--){
		scanf("%d",&n);
		Matrix res=__pow(mat,n-2),ans;
		ans.Init();
		for(int i=1;i<=1;++i){
			for(int j=1;j<=9;++j){
				for(int k=1;k<=9;++k){
					ans.mp[i][k]=(ans.mp[i][k]+(long long)bg[i][j]*res.mp[j][k])%mod;
				}
			}
		}
		int anss=0;
		for(int i=1;i<=9;++i){
			anss=(anss+ans.mp[1][i])%mod;
		}
		printf("%d\n",anss);
	}
	return 0;
}

---

Task 3：雪

【问题描述】

 小H喜欢堆雪堆，在一共N天的寒假里，她在第i天会堆一个体积为Vi的雪堆。

 雪堆每天都会融化一部分，准确地讲，如果这天的气温是Ti，那么每个堆好的雪堆的体积都会减少Ti。如果某个雪堆的体积减到了0，那么它便会消失。

 小H想知道每天总共融化的雪的体积是多少。

【输入】

 第一行为1个正整数N。

 第二行为N个正整数Vi。

 第三行为N个整整数Ti。

【输出】

 共N行每行一个整数表示当天融化的雪的总体积。

【输入输出样例】

5 

30 25 20 15 10 

9 10 12 4 13 

ans：9 20 35 11 25

【数据范围】

• 1 – 4 1 ≤ N ≤ 100
• 5 - 6 1 ≤ N ≤ 1000
• 7 - 10 1 ≤ N ≤ 100000

 对于100%的数据：0 ≤ Vi, Ti ≤ 109。

 大水题，没有想象中那么复杂，直观想法就可以跑过去。

 维护气温的前缀和，二分答案找到第i天堆的雪人会在哪天化掉。在这一天特殊处理，其他天都是完整的化掉一个气温大小的体积，所以丢进树状数组差分维护即可。

 树状数组大法吼啊！！！

#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define MAXN 100010
#define lint long long
using namespace std;
lint n,V[MAXN],T[MAXN],sum[MAXN],ans[MAXN],Tree[MAXN];
inline lint read(){
	lint s=0;
	char ch=getchar();
	while('9'<ch||ch<'0'){
		ch=getchar();
	}
	while('0'<=ch&&ch<='9'){
		s=s*10+ch-'0';
		ch=getchar();
	}
	return s;
}
inline lint lowbit(lint x){
	return x&-x;
}
inline void add(lint pos,lint val){
	while(pos<=n){
		Tree[pos]+=val;
		pos+=lowbit(pos);
	}
}
inline lint getsum(lint pos){
	lint ans=0;
	while(pos){
		ans+=Tree[pos];
		pos-=lowbit(pos);
	}
	return ans;
}
int main(){
	freopen("snow.in","r",stdin);
	freopen("snow.out","w",stdout);
	n=read();
	for(register int i=1;i<=n;++i){
		V[i]=read();
	}
	for(register int i=1;i<=n;++i){
		T[i]=read();
		sum[i]=sum[i-1]+T[i];
		//维护一个时间的前缀和
	}
	for(register int i=1;i<=n;++i){
		//day i:build V[i],melt T[i]
		lint pos=lower_bound(sum+1,sum+1+n,V[i]+sum[i-1])-sum;
		ans[pos]+=V[i]-(sum[pos-1]-sum[i-1]);
		add(i,1);
		add(pos,-1);
	}
	for(register int i=1;i<=n;++i){
		ans[i]+=getsum(i)*T[i];
		printf("%lld ",ans[i]);
	}
	return 0;
}