python买卖股票的最佳时机--贪心/蛮力算法简介

开始刷leetcode算法题 今天做的是“买卖股票的最佳时机”

题目要求

给定一个数组，它的第 i 个元素是一支给定股票第 i 天的价格。

设计一个算法来计算你所能获取的最大利润。你可以尽可能地完成更多的交易（多次买卖一支股票）。

注意：你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。

看到这个题目 最初的想法是蛮力法

　　通过两层循环 不断计算不同天之间的利润及利润和

下面上代码

 class Solution(object):
     def maxProfit(self, prices):
         """
         :type prices: List[int]
         :rtype: int
         """

         self.allbuy1 = []    #单次买卖的差值数组 （可能为负）
         self.allbuy2 = []    #所有可能买卖的利润数组 （可能为负）
                              # allbuy1和allbuy2的区别为一个是单次买卖 一个是多次买卖和
         self.curbuy(prices,0,0) #prices 为价格表 0：初始 0：
         #print(self.allbuy1)
         #print(self.allbuy2)
         return  self.picBigest(self.allbuy2)
     def buyticket(self,prilist,a,b):       #list:放入的价格数组 a:上一次买入的价格 b:今天卖出的价格
         return  prilist[b] -prilist[a]   #返回 赚取得价格

     def curbuy(self,plist,x,result): #plist：价格数组 x:当天的数组坐标 result: 利润
         obj=result                     #固定上一次的价格 保存为上一个递归
         lens=len(plist)                #天数
         for i in range(x,lens-1):
             for j in range(i+1,lens):
                 temp=self.buyticket(plist,i, j)
                 self.allbuy1.append(temp)
                 self.allbuy2.append(temp)     #单次利润放入数组
                 result = obj + temp     #将之前的利润加上今天的利润
                 if(x>=2):             #如果买入是第2+1天以后  则可以加上之前的利润
                     self.allbuy2.append(result)  #多次买卖利润放入数组
                 self.curbuy(plist,j+1,result)   #递归 j+1:卖出的后一天 result:利润

     def picBigest(self,reslist):
         big=0
         for i in reslist:
             if (i>big):
                 big=i
         print(big)
         return big

 if __name__ == '__main__':
         test=Solution()
         prices = [5,7,3,8]  # 输入的每日股票数组
         test.maxProfit(prices)

分析：

这个代码理解起来简单 就是将所有可能都放入数组中 找出最大一个可能

将这个代码提交时 显示 超出时间限制 确实 如果输入的数组长度非常大时 计算量巨大 出现错误

——————————————————————————————————————————————————————————————————————————————

更换思路：利用贪心算法解决此事

首先介绍 一下贪心算法： 对问题只对当前情况进行最优解处理，之后发生什么对之前的决定都不改变。简单的说就是一个局部最优解的过程

介绍个例子就明白了：  找零钱问题

假设有面值为5元、2元、1元、5角、2角、1角的货币，需要找给顾客4元6角现金，为使付出的货币的数量最少

　　首先找出小于4元6角的最大面值（2元）

　　其次找出小于2元6角的最大面值（2元）

　　接着找出小于6角的最大面值（5角）

　　最后找出小于1角的最大面值（1角） ---付出4张纸币

介绍完了贪心算法简单思想 就利用该方法解决对应问题

在已知股票价格走势情况下 只需要对下一天进行判断 如果涨了 则买 如果跌了则卖 这样收益会保持固定增长

当然了 有人会提出 我可以选择不卖等几天再卖 或不买等几天再买 的方式 一样可以保持增长 但是如图

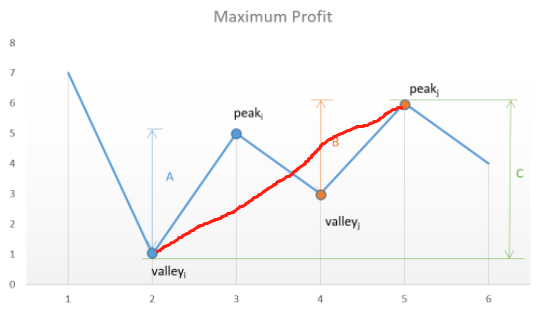
如果在第2天买入 3天卖出 4天买入 5天卖出 收益为A+B

如果在第2天买入 5天卖出 收益为 C

明显得出A+B大于C          所以贪心法在这种情况非常适用并且肯定得到最优解

直接上代码

 class Solution(object):
     def maxProfit(self, prices):
         profit = 0
         for day in range(len(prices)-1):
             differ = prices[day+1] - prices[day]
             if differ > 0:
                 profit += differ
         return profit
 if __name__ == '__main__':
         test=Solution()
         prices = [5,7,3,9]  # 输入的每日股票数组
         print(test.maxProfit(prices))