机器学习：SVM（scikit-learn 中的 RBF、RBF 中的超参数 γ）

一、高斯核函数、高斯函数

• 
• μ：期望值，均值，样本平均数；（决定告诉函数中心轴的位置：x = μ）
• σ²：方差；（度量随机样本和平均值之间的偏离程度：， 为总体方差，  为变量，  为总体均值，  为总体例数）

1. 实际工作中，总体均数难以得到时，应用样本统计量代替总体参数，经校正后，样本方差计算公式：S^2= ∑(X-  ) ^2 / (n-1)，S^2为样本方差，X为变量，  为样本均值，n为样本例数。

• σ：标准差；（反应样本数据分布的情况：σ 越小高斯分布越窄，样本分布越集中；σ 越大高斯分布越宽，样本分布越分散）
• γ = 1 / (2σ²)：γ 越大高斯分布越窄，样本分布越集中；γ 越小高斯分布越宽，样本分布越密集；

二、scikit-learn 中的 RBF 核

　1）格式

• from sklearn.svm import SVC
  
  svc = SVC(kernel='rbf', gamma=1.0)

  # 直接设定参数 γ = 1.0；

　2）模拟数据集、导入绘图函数、设计管道

• 此处不做考察泛化能力，只查看对训练数据集的分类的决策边界，不需要进行 train_test_split；

• 模拟数据集

  import numpy as np
  import matplotlib.pyplot as plt
  
  from sklearn import datasets
  
  X, y = datasets.make_moons(noise=0.15, random_state=666)
  
  plt.scatter(X[y==0, 0], X[y==0, 1])
  plt.scatter(X[y==1, 0], X[y==1, 1])
  plt.show()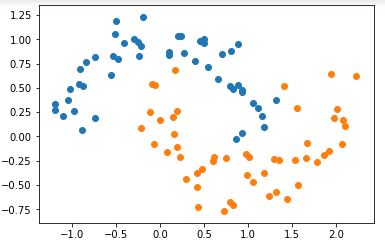

  

• 导入绘图函数

  def plot_decision_boundary(model, axis):
  
      x0, x1 = np.meshgrid(
          np.linspace(axis[0], axis[1], int((axis[1]-axis[0])*100)).reshape(-1,1),
          np.linspace(axis[2], axis[3], int((axis[3]-axis[2])*100)).reshape(-1,1)
      )
      X_new = np.c_[x0.ravel(), x1.ravel()]
  
      y_predict = model.predict(X_new)
      zz = y_predict.reshape(x0.shape)
  
      from matplotlib.colors import ListedColormap
      custom_cmap = ListedColormap(['#EF9A9A','#FFF59D','#90CAF9'])
  
      plt.contourf(x0, x1, zz, linewidth=5, cmap=custom_cmap)

• 设计管道

  from sklearn.preprocessing import StandardScaler
  from sklearn.svm import SVC
  from sklearn.pipeline import Pipeline
  
  def RBFKernelSVC(gamma=1.0):
      return Pipeline([
          ('std_scaler', StandardScaler()),
          ('svc', SVC(kernel='rbf', gamma=gamma))
      ])

　3）调整参数 γ，得到不同的决策边界

• γ == 0.1

  svc_gamma_01 = RBFKernelSVC(gamma=0.1)
  svc_gamma_01.fit(X, y)
  
  plot_decision_boundary(svc_gamma_01, axis=[-1.5, 2.5, -1.0, 1.5])
  plt.scatter(X[y==0, 0], X[y==0, 1])
  plt.scatter(X[y==1, 0], X[y==1, 1])
  plt.show()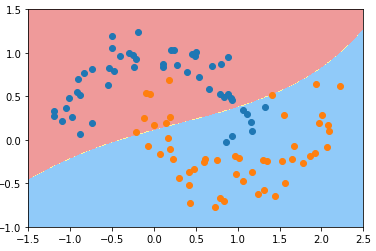

  

• γ == 0.5

  svc_gamma_05 = RBFKernelSVC(gamma=0.5)
  svc_gamma_05.fit(X, y)
  
  plot_decision_boundary(svc_gamma_05, axis=[-1.5, 2.5, -1.0, 1.5])
  plt.scatter(X[y==0, 0], X[y==0, 1])
  plt.scatter(X[y==1, 0], X[y==1, 1])
  plt.show()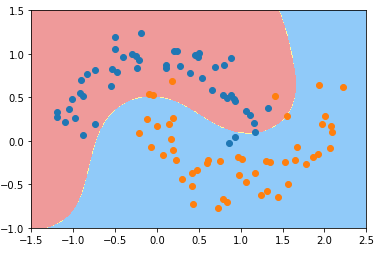

  

• γ == 1

  svc_gamma_1 = RBFKernelSVC(gamma=1.0)
  svc_gamma_1.fit(X, y)
  
  plot_decision_boundary(svc_gamma_1, axis=[-1.5, 2.5, -1.0, 1.5])
  plt.scatter(X[y==0, 0], X[y==0, 1])
  plt.scatter(X[y==1, 0], X[y==1, 1])
  plt.show()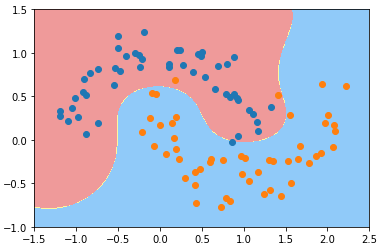

  

• γ == 10

  svc_gamma_10 = RBFKernelSVC(gamma=10)
  svc_gamma_10.fit(X, y)
  
  plot_decision_boundary(svc_gamma_10, axis=[-1.5, 2.5, -1.0, 1.5])
  plt.scatter(X[y==0, 0], X[y==0, 1])
  plt.scatter(X[y==1, 0], X[y==1, 1])
  plt.show()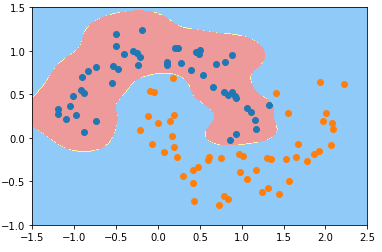

  

• γ == 100

  svc_gamma_100 = RBFKernelSVC(gamma=100)
  svc_gamma_100.fit(X, y)
  
  plot_decision_boundary(svc_gamma_100, axis=[-1.5, 2.5, -1.0, 1.5])
  plt.scatter(X[y==0, 0], X[y==0, 1])
  plt.scatter(X[y==1, 0], X[y==1, 1])
  plt.show()

  

　4）分析

• 随着参数 γ 从小到大变化，模型经历：欠拟合——优——欠拟合；

• γ == 100 时：

1. 现象：每一个蓝色的样本周围都形成了一个“钟形”的图案，蓝色的样本点是“钟形”图案的顶部；
2. 原因：γ 的取值过大，样本分布形成的“钟形”图案比较窄，模型过拟合；
3. 决策边界几何意义：只有在“钟形”图案内分布的样本，才被判定为蓝色类型；否则都判定为黄山类型；

• γ == 10 时，γ 值减小，样本分布规律的“钟形”图案变宽，不同样本的“钟形”图案区域交叉一起，形成蓝色类型的样本的分布区域；

• 超参数 γ 值越小模型复杂度越低，γ 值越大模型复杂度越高；