OpenCASCADE直线与平面求交

OpenCASCADE直线与平面求交

在《解析几何》相关的书中都给出了直线和平面的一般方程和参数方程。其中直线的一般方程有点向式形式的。

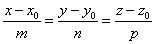
由于过空间一点可作且只能作一条直线平行于已知直线，所以当直线上一点（x0, y0, z0)和它的一方向向量（m,n,p)为已知时，直线就完全确定了。所以在OpenCASCADE中直线类gp_Lin有一个构造函数：

gp_Lin (const gp_Pnt &P, const gp_Dir &V) 即通过点和方向来构造直线。由直线的点向式方程容易导出直线的参数方程：

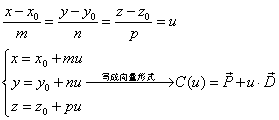
其中OpenCASCADE的直线是用参数方程来表示的。

同理对于平面而言，过空间一点可以作而且只能作一平面垂直于一已知直线，所以平面的一点（x0,y0,z0)和它的一个法线方向(A, B, C)为已知时，平面就完全确定了。所以平面方程也有点向式的：

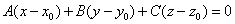
从一个点和两个不共线的向量确定一个平面作为讨论的出发点，可以得出平面的参数方程：

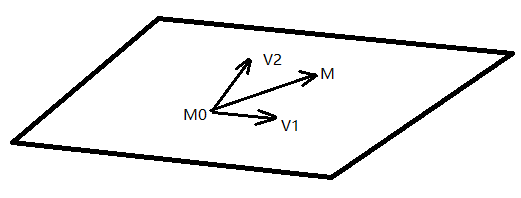
如上图所示，已知一个点M0(x0,y0,z0)，向量v1(x1,y1,z1)和向量v2(x2,y2,z2)，我们来求点M0和向量V1，V2确定的平面方程。点M(x,y,z)在平面上的充要条件是向量M0M与V1, V2共面。因为向量V1, V2不平行，所以共面的充要条件是存在唯一的一对实数u, v使：

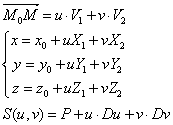
向量M0M和V1，V2共面的充要条件是：

根据平面的参数方程可知，要确定一个平面从参数方程的角度来看需要一个点和两个方向。从参数方程推导出一般方程的过程也是计算平面一般方程系数的方法。

根据直线的参数方程及平面的一般方程可以推导出直线与平面交点的计算公式，推导过程如下：

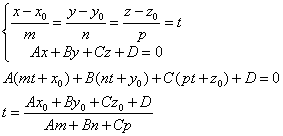
从上面的推导过程可以看出，计算直线与平面的交点主要就是计算参数t，当t求出后代入直线参数方程即可得到交点坐标。从参数t的计算公式可知，有个特殊情况就是分母为零的情况，此时是直线与平面平行共面需要特别处理。

在OpenCASCADE中提供了直线与平面求交的计算类IntAna_IntConicQuad，其实现源码如下：

void IntAna_IntConicQuad::Perform (const gp_Lin& L, const gp_Pln& P,
                                   const Standard_Real Tolang,
                                   const Standard_Real Tol,
                                   const Standard_Real Len) {

  // Tolang represente la tolerance angulaire a partir de laquelle on considere
  // que l angle entre 2 vecteurs est nul. On raisonnera sur le cosinus de cet
  // angle, (on a Cos(t) equivalent a t au voisinage de Pi/2).

  done=Standard_False;

  Standard_Real A,B,C,D;
  Standard_Real Al,Bl,Cl;
  Standard_Real Dis,Direc;

  P.Coefficients(A,B,C,D);
  gp_Pnt Orig(L.Location());
  L.Direction().Coord(Al,Bl,Cl);

  Direc=A*Al+B*Bl+C*Cl;
  Dis = A*Orig.X() + B*Orig.Y() + C*Orig.Z() + D;
  //
  parallel=Standard_False;
  if (Abs(Direc) < Tolang) {
    parallel=Standard_True;
    if (Len!= && Direc!=) {
      //check the distance from bounding point of the line to the plane
      gp_Pnt aP1, aP2;
      //
      aP1.SetCoord(Orig.X()-Dis*A, Orig.Y()-Dis*B, Orig.Z()-Dis*C);
      aP2.SetCoord(aP1.X()+Len*Al, aP1.Y()+Len*Bl, aP1.Z()+Len*Cl);
      if (P.Distance(aP2) > Tol) {
        parallel=Standard_False;
      }
    }
  }
  if (parallel) {
    if (Abs(Dis) < Tolang) {
      inquadric=Standard_True;
    }
    else {
      inquadric=Standard_False;
    }
  }
  else {
    parallel=Standard_False;
    inquadric=Standard_False;
    nbpts = ;
    paramonc [] = - Dis/Direc;
    pnts[].SetCoord(Orig.X()+paramonc[]*Al,
                     Orig.Y()+paramonc[]*Bl,
                     Orig.Z()+paramonc[]*Cl);
  }
  done=Standard_True;
}

从上述代码中可以看出其计算思路也是先计算参数t，还加了一个特殊用法，即当参数Len!=0且参数t的分母!=0时重新判断直线与平面的平行状态。这个用法虽然有平行状态的重新判断，但是如果不平行没有计算交点的处理。所以使用这个函数时，参数Len可以用默认值0，即不用这段处理逻辑。还有个不严谨的地方是这里的实数判断没有用区间判断法。