Copying GC (Part two :Multi Space Copying GC)

目录

• 近似深度优先搜索方法
  • Cheney的GC复制算法
  • 前提
  • 执行结果
• 多空间复制算法
  • multi_space_copying()函数
  • mark_or_copy()
  • copy()
  • 执行过程
  • 优缺点

近似深度优先搜索方法

Paul R.Wilson、Michael S.Lam、Thomas G.Moher,1991

这个方法只是近似深度优先搜索，但可以做到深度优先执行GC复制算法。

Cheney的GC复制算法

假设所有对象都是2个字，下图所示是对象间的引用关系。

下图所示是执行该算法时候，各个对象所在的页面（页面，在操作系统，和计算机组成原理课程中都有）。

右上角数字是页面编号，假如说页面容量是6个字（只能放3个对象）。

从上图不难看出，A,B,C是相邻的，这就是比较理想的状态。对于其他对象来说，降低了连续读取的可能性，降低了缓存命中率。

在下面1-4页中，同一个页面的对象甚至都没有引用关系（页面1中D和页面2中HI，有引用关系，但是不命中，需要读内存数据到catch），这样就不得不从内存上再去读。一直这样下去可想而知，有很多的对象会是这样的分布状态。

前提

在这个方法中有下面四个变量。

• $page: 将堆分割成一个个页面的数组。$page[i]指向第i个页面的开头。
• $local_scan：将每个页面中搜索用的指针作为元素的数组。$local_scan[i]指向第i个页面中下一个应该搜索的位置。
• $major_scan：指向搜索尚未完成的页面开头的指针。
• $free：指向分块开头的指针。

先复制A到To空间，然后复制他们的孩子B,C，都被放置到了0页。如下图示：

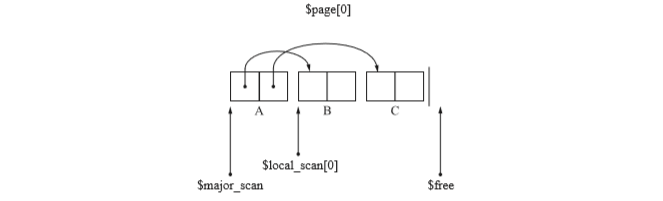
• 因为A已经搜索完毕，所以$local_scan[0]指向B。
• $free指向第一页的开头，也就是说下一次复制对象会被安排在新的页面。在这种情况下，程序会从$major_scan引用的页面和$local_scan开始搜索。
• 当对象被复制到新页面时，程序会根据这个页面的$local_scan进行搜索，直到新页面对象被完全占满为止。
• 此时因为$major_scan还指向第0页，所以还是从$local_scan[0]开始搜索，也就是说要搜索B。

• 复制了D（B引用的对象），放到了$page[1]开头。像这样的页面放在开头时候，程序会使用该页面的$local_scan进行搜索。此时$local_scan[0]暂停，$local_scan[1]开始。之后复制了H,I。

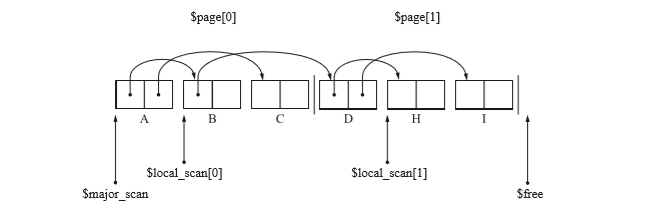
• 这里第一页满了，所以$free指向第二页开头。因此$local_scan[1]暂停搜索，程序$local_scan[0]开始搜索。（即对B对象再次进行搜索，看有没有其他孩子。）

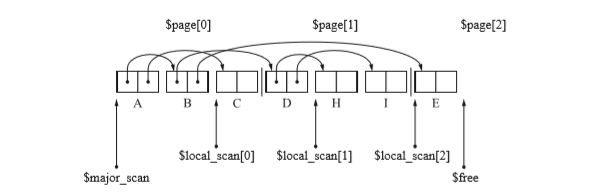
• 可以看到B的孩子E被复制到了$page[2],同样，对$local_scan[0]再次进行暂停，对E用local_scan[2]进行搜索。
• 因此复制了J,K。

• 通过对J,K的搜索页面2满了，$free指向了页面3。再次回到$local_scan[0]进行搜索。
• 搜索完对象C，复制完A到O的所有对象之后状态如下图所示。

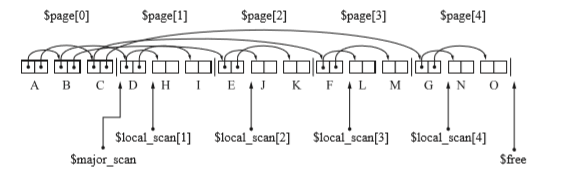
这样就搜索完了第0页($major_scan),虽然还没有搜索完子对象，但是孩子没有孩子，所以现在这个状态，和搜索完后是一样的。

执行结果

该方法是如何安排对象的呢？如下图示：

很明显能看出与Cheney的复制算法不同，不管下一个页面在哪里，对象之间都存在引用关系。

该方法，采用了不完整的广度优先，它实际上是用到了暂停的。从一开始我们就根据关系，然后进行暂停，将有关系的对象安排到了一个页面中。

多空间复制算法

GC复制算法最大的缺点就是只能利用半个堆。

但是如果我们把空间分成十份，To空间只占一份那么这个负担就站到了整体的1/10。剩下的8份是空的，在这里执行GC标记清除算法。

多空间复制算法，实际上就是把空间分成N份，对其中两份进行GC复制算法，对其中(N-2)份进行GC标记-清除。

multi_space_copying()函数

muti_space_copying(){
    $free = $heap[$to_space_index]
    for(r :$roots)
        *r = mark_or_copy(*r)

    for(index :0..(N-1))
        if(is_copying_index(index) == FALSE)
            sweep_block(index)

    $to_space_index = $from_space_index
    $from_space_index = ($from_space_index +1) % N
}

将堆分为N等份，分别是$heap[0],$heap[1]...$heap[N-1]。这里的$heap[$to_space_index]表示To空间，每次执行GC时，To空间都会像$heap[0],$heap[1]...$heap[N-1]，$heap[0],这样进行替换。Form空间在To空间的右边，也就是$heap[1]...$heap[N-1]。

• 其中第一个for循环，为活动对象打上标记。能看出来是标记清除算法中的一个阶段。
• 其中第一个for循环，当对象在From空间时，mark_or_copy()函数会将其复制到To空间，返回复制完毕的对象。如果obj在除Form空间以外的其他地方mark_or_copy()会给其打上标记，递归标记或复制它的子对象。
• 其中第二个for循环，是清除阶段。对除From和To空间外的其他空间，把没有标记的对象连接到空闲链表。
• 最后将To和From空间向右以一个位置，GC就结束了。

mark_or_copy()

mark_or_copy(obj){
    if(is_pointer_to_from_space(obj) == True)
        return copy(obj)
    else
        if(obj.mark == FALSE)
            obj.mark == TRUE
            for(child :children(obj))
                *child = mark_or_copy(*child)
        return obj

}

调查参数obj是否在From空间里。如果在From空间里，那么它就是GC复制算法的对象。这时就通过copy()函数复制obj，返回新空间的地址。

如果obj不在From空间里，它就是GC标记-清除算法的对象。这时要设置标志位，对其子对象递归调用mark_or_copy()函数。最后不要忘了返回obj。

copy()

copy(obj){
    if(obj.tag != COPIED)
        copy_data($free, obj, obj.size)
        obj.tag = COPIED
        obj.forwarding = $free
        $free += obj.size
        for(child :children(obj.forwarding))
            *child = mark_or_copy(*child)
        return obj.forwarding
}

递归调用不是copy()函数，而是调用mark_ or_copy()函数。如果对象*child是复制对象，则通过mark_or_copy() 函数再次调用这个copy()函数。

执行过程

将内存分为4等份。如下图示：

To空间$heap[0]空着，其他三个都被占用。这个状态下，GC就会变为如下如示：

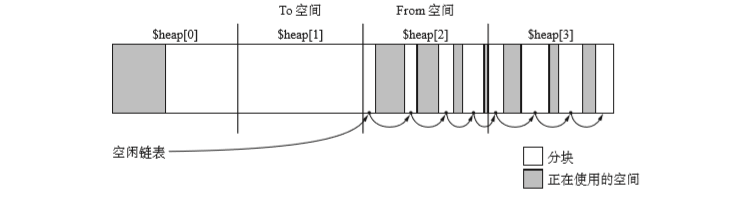
我们将$heap[0]作为To空间，将$heap[1]作为From空间执行GC复制算法。此外$heap[2]和$heap[3]中执行GC标记-清除算法，将分块连接到空闲链表。

当mutator申请分块时候，程序会从空闲链表或者$heap[0]中分割出块给mutator。

接下来，To空间和From空间都向后移动一个位置。mutator重新开始。

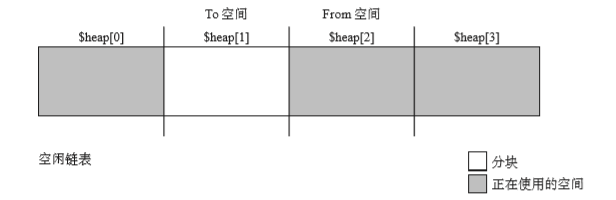
这次$heap[1]是To空间，$heap[2]From空。这种状态下执行就会变为下图所示：

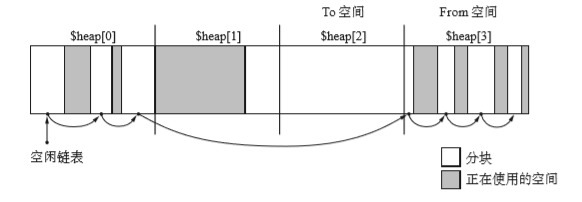
$heap[2]的活动对象都被复制到了$heap[1]中，在$heap[0]和$heap[3]中执行GC标记清除。然后From和To后移一次。

优缺点

优点

提高内存利用率：没有将内存空间二等分，而是分割了更多空间。

缺点

GC标记清除，分配耗时，分块碎片化。当GC标记清除算法的空间越小的时候，该问题表现的越不突出。例如将内存分为3份的情况下。