python学习笔记:第六天

一、元组（通用格式a=(1,),结束后面加个逗号,不同与数组是中括号，只能是只读的，不能修改，是有序的）：

1. 列表之间可以嵌套(列表之间嵌套，嵌套元组，是有序的):a[b[1,2],c[3,4]],输出1的话，a[0][0];

二、enumerate(),在列表加上序列，enumerate(列表,从几开始)

三、a,b=[2,3]分别将2赋予a,3赋予b.

四、输出列表长度：len(列表名)

五、字典（dictionary），是无序列表

1．格式：dic1={‘键1’:’值1’,’键2’:’值2’}，并且键是不可修改的

2．dic2=dict(((‘键1’,值1’),))，创建字典

3．字典操作：

（1）增：

dic1 = {}

Dic1[‘name’]=liuhui

Dic1.setdefalut(‘age’,’18’),增加之后返回，有返回值，输出值。键存在，不该懂，返回字典中键对应的值。

（2）查：

.keys()输出键，不是一个列表

List(dic.keys())将键转换为列表

Dic[‘键’]

.values()输出值，

.items()输出键值对，组成元组输出

（3）删：

.clear()清空字典，没有数据

Del dic1[‘键’]通过键，删除键值对

.pop(‘键’)通过键删除指定键值对，并返回删除的键值对。

Dic1.popitem(),随机删除一个键值对，并返回删除的键值对

Del dic,删除整个字典

（4）改：

dic1.update(dic2):将字典2添加到字典1中，如果有相同键值对，字典2中覆盖字典1中的键值

（5）Dic1 = dict.fromkeys([‘键1’，’键2’，’键3’],’test’),test也可以是列表

（6）字典嵌套

（7）排序：sorted(dic),根据键排序，从小到大排序。

Sorted(dic.values()),对值进行排序

Sorted(dic.items()),根据键排序

（8）字典的便利：

①

　　　　

②

　　　　

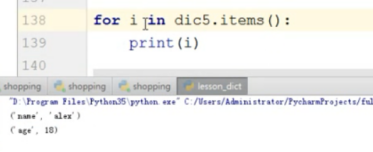
六、字符串（可以使单引号，也可以是双引号）：

Print(‘hello’*2)输出2遍

Print(‘helloworld’[2:])从索引第二个打印到最后一个

用In判断一个字符串是否在列表中，也可以判断字符串是否包含某个字符串

字符串拼接：

1. 可以用+（效率太低）

A=’12’

B=’34’

C=A+B

C=1234

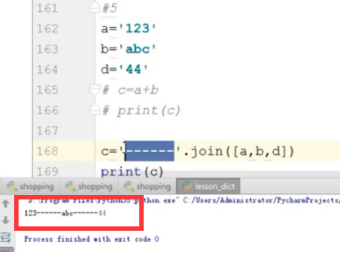
1. .join()

　　　　　　 

　　　　

字符串内置方法：str=’helloworld’

1. str.count(‘ll’)，输出ll多少个
2. Str.capitalize(),字符串首字母大写
3. Str.center(20,’-’),打印20个字符，除了helloworld，其他用-代表，并且字符串居中
4. str.encode()解码和编码
5. Str.endswith(‘ld’)代表以某个字符串结尾，相同味true不同味false
6. Str.startswith(‘’)代表以某个字符串开头，相同味true，不同为false
7. Str.expandtabs()
8. Str.find(‘’)查找某个字符串内容，并将索引值返回
9. Str.format()

Str = ‘hello {name}’

Print(Str.format(name==’阿辉’)

结果：hello 阿辉

1. Str.format_map({‘name’:’阿辉’,’age’:18})

Str = ‘hello {name} is {age}’

Print(tr.format_map({‘name’:’阿辉’,’age’:18})

结果：hello 阿辉 is 18

1. Str.index()查找某个元素的索引值，如果没有则报错
2. Str.isalnum()判断字符串是否包含数字或者字母。
3. Str.isdecimal()判断是不是十进制数
4. Str.isdigit()判断是不是整型
5. Str.isnumeric()判断是不是整数
6. Str.isidentifier()判断是不是一个非法字符
7. Str.islower()判断是不是全小写
8. Str.upper()判断是不是全大写
9. Str.isspace()是不是空格
10. Str.istitle() 每个字母的首字母必须大写
11. Str.title()将字符串转换为标题格式
12. Str.lower()字符串所有大写变小写
13. Str.upper() 字符串小写变大写
14. Str.swapcase()把大写变小写，小写变大写
15. Str.ljust(10,’*’)左对齐
16. Str.rjust(10,’*’)右对齐
17. Str.strip()将字符串中左右空格，换行符去掉
18. Str.lstrip()去掉左边空格，换行符去掉
19. Str.rstrip()去掉右边空格，换行符去掉
20. Str.replace(‘元素1’,’元素2’,num)将元素1替换元素2,num是替换几次
21. Str.rfind(‘元素1’)
22. Str.split(‘’)将字符串分割