poj 1021矩阵平移装换后是否为同一个矩阵

2D-Nim

Time Limit: 1000MS		Memory Limit: 10000K
Total Submissions: 3081		Accepted: 1398

Description

The 2D-Nim board game is played on a grid, with pieces on the grid points. On each move, a player may remove any positive number of contiguous pieces in any row or column. The player who removes the last piece wins. For example, consider the left grid in the following figure.


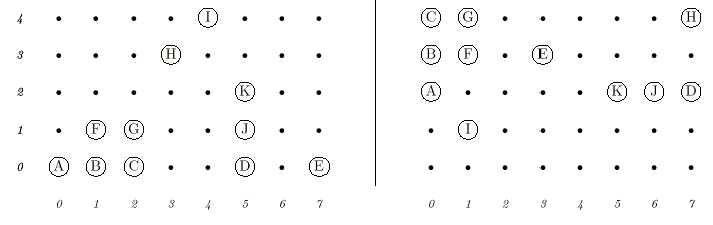
The player on move may remove (A), (B), (A, B), (A, B, C), or (B,F), etc., but may not remove (A, C), (D, E), (H, I) or (B, G).

For purposes of writing 2D-Nim-playing software, a certain
programmer wants to be able to tell whether or not a certain position
has ever been analyzed previously. Because of the rules of 2D-Nim, it
should be clear that the two boards above are essentially equivalent.
That is, if there is a winning strategy for the left board, the same one
must apply to the right board. The fact that the contiguous groups of
pieces appear in different places and orientations is clearly
irrelevant. All that matters is that the same clusters of pieces (a
cluster being a set of contiguous pieces that can be reached from each
other by a sequence of one-square vertical or horizontal moves) appear
in each. For example, the cluster of pieces (A, B, C, F, G) appears on
both boards, but it has been reflected (swapping left and right),
rotated, and moved. Your task is to determine whether two given board
states are equivalent in this sense or not.

Input

The
first line of the input file contains a single integer t (1 ≤ t ≤ 10),
the number of test cases, followed by the input data for each test case.
The first line of each test case consists of three integers W, H, and n
(1 ≤ W, H ≤ 100). W is the width, and H is the height of the grid in
terms of the number of grid points. n is the number of pieces on each
board. The second line of each test case contains a sequence of n pairs
of integers xi , yi, giving the coordinates of the pieces on the first
board (0 ≤ xi < W and 0 ≤ yi < H). The third line of the test case
describes the coordinates of the pieces on the second board in the same
format.

Output

Your
program should produce a single line for each test case containing a
word YES or NO indicating whether the two boards are equivalent or not.

Sample Input

2
8 5 11
0 0 1 0 2 0 5 0 7 0 1 1 2 1 5 1 3 3 5 2 4 4
0 4 0 3 0 2 1 1 1 4 1 3 3 3 5 2 6 2 7 2 7 4
8 5 11
0 0 1 0 2 0 5 0 7 0 1 1 2 1 5 1 3 3 6 1 4 4
0 4 0 3 0 2 1 1 1 4 1 3 3 3 5 2 6 2 7 2 7 4

Sample Output

YES
NO

问的是点阵图的同构。

应该有比较科学的方法的，但是我看到网上有一个做法是统计十字走的步数的方法。觉得非常神奇。虽然看起来不怎么科学，但是可能是数据比较水，居然能A。大致思路就是统计每个点能向四个方向走的步数的和，再比较这两个图中每个点是否都能找到一个总步数相同的点与之匹配

#include <iostream>
#include <string.h>
#include <stdio.h>
#include <algorithm>

using namespace std;
struct node
{
    int x;
    int y;
} p[];

int map[][],n,w,h;
int sum[][];

int main()
{
    int t;
    scanf("%d",&t);
    while(t--)
    {
        cin>>w>>h>>n;
        memset(map,,sizeof(map));
         memset(sum,,sizeof(sum));
        for(int i=; i<=n; i++)
        {
            cin>>p[i].x>>p[i].y;
            map[p[i].x][p[i].y]=;
        }
        for (int i = ; i <= n; i ++)
        {
            int xx = p[i].x,yy = p[i].y,x,y,cnt = ;
            for (x = xx,y = yy; map[x][y] && y < h; ++y,++cnt);
            for (x = xx,y = yy; map[x][y] && x < w; ++x,++cnt);
            for (x = xx,y = yy; map[x][y] && y >= ; --y,++cnt);
            for (x = xx,y = yy; map[x][y] && x >= ; --x,++cnt);
            sum[][i] = cnt;
        }
        memset(map,,sizeof(map));
        for(int i=; i<=n; i++)
        {

            cin>>p[i].x>>p[i].y;
            map[p[i].x][p[i].y]=;
        }
        for (int i = ; i <= n; i ++)
        {
            int xx = p[i].x,yy = p[i].y,x,y,cnt = ;
            for (x = xx,y = yy; map[x][y] && y < h; ++y,++cnt);
            for (x = xx,y = yy; map[x][y] && x < w; ++x,++cnt);
            for (x = xx,y = yy; map[x][y] && y >= ; --y,++cnt);
            for (x = xx,y = yy; map[x][y] && x >= ; --x,++cnt);
            sum[][i] = cnt;
        }

        sort(sum[]+,sum[]++n);
        sort(sum[]+,sum[]++n);

        int falg=;
        for(int i=; i<n; i++)
        {
            if(sum[][i]!=sum[][i])
            {
                falg=;
                break;
            }
        }
        if(!falg)
            cout<<"NO"<<endl;
        else
            cout<<"YES"<<endl;
    }
    return ;
}

思路：把每个点的值设为连续的x轴点数和连续的y轴点数之和。排序之后，如果相等，则两个图相等。证明的话可想而知

过程：一次A了

代码：
#include
#include

int x[],y[];
int map[][];
int left[],right[];

int main(){
    int cas;
    int i,j,k;
    int w,h,n;
    int tmp;

    scanf("%d",&cas);
    for(i = ; i < cas; i++){
        scanf("%d%d%d",&w,&h,&n);

        memset(map,,sizeof(map));
        for(j = ; j < n; j++){
            scanf("%d%d",&x[j],&y[j]);
            map[x[j]][y[j]] = ;
        }

        memset(left,,sizeof(left));
        for(j = ; j < n; j++){
            tmp = x[j];
            while(tmp >= &&map[tmp][y[j]] == ){
                left[j]++;
                tmp--;
            }

            tmp = x[j]+;
            while(tmp < w&&map[tmp][y[j]] == ){
                left[j]++;
                tmp++;
            }

            tmp = y[j]-;
            while(tmp >= &&map[x[j]][tmp] == ){
                left[j]++;
                tmp--;
            }

            tmp = y[j]+;
            while(tmp < h&&map[x[j]][tmp] == ){
                left[j]++;
                tmp++;
            }
        }

        memset(map,,sizeof(map));
        for(j = ; j < n; j++){
            scanf("%d%d",&x[j],&y[j]);
            map[x[j]][y[j]] = ;
        }
        memset(right,,sizeof(right));
        for(j = ; j < n; j++){
            tmp = x[j];
            while(tmp >= &&map[tmp][y[j]] == ){
                right[j]++;
                tmp--;
            }

            tmp = x[j]+;
            while(tmp < w&&map[tmp][y[j]] == ){
                right[j]++;
                tmp++;
            }

            tmp = y[j]-;
            while(tmp >= &&map[x[j]][tmp] == ){
                right[j]++;
                tmp--;
            }

            tmp = y[j]+;
            while(tmp < h&&map[x[j]][tmp] == ){
                right[j]++;
                tmp++;
            }
        }

        for(j = ; j < n; j++){
            for(k = ; k < n; k++){
                if(left[k-] < left[k]){
                    tmp = left[k-];
                    left[k-] = left[k];
                    left[k] = tmp;
                }
            }
        }

        for(j = ; j < n; j++){
            for(k = ; k < n; k++){
                if(right[k-] < right[k]){
                    tmp = right[k-];
                    right[k-] = right[k];
                    right[k] = tmp;
                }
            }
        }

        for(j = ; j < n; j++){
            if(left[j] != right[j]) break;
        }

        if(j == n){
            printf("YES\n");
        }else{
            printf("NO\n");
        }
    }

    return ;
}