2016/10/28 很久没更了 leetcode解题 3sumcloset

16.3Sum Closest

Given an array S of n integers, find three integers in S such that the sum is closest to a given number, target. Return the sum of the three integers. You may assume that each input would have exactly one solution.

    For example, given array S = {-1 2 1 -4}, and target = 1.

    The sum that is closest to the target is 2. (-1 + 2 + 1 = 2).
附上自己的解题

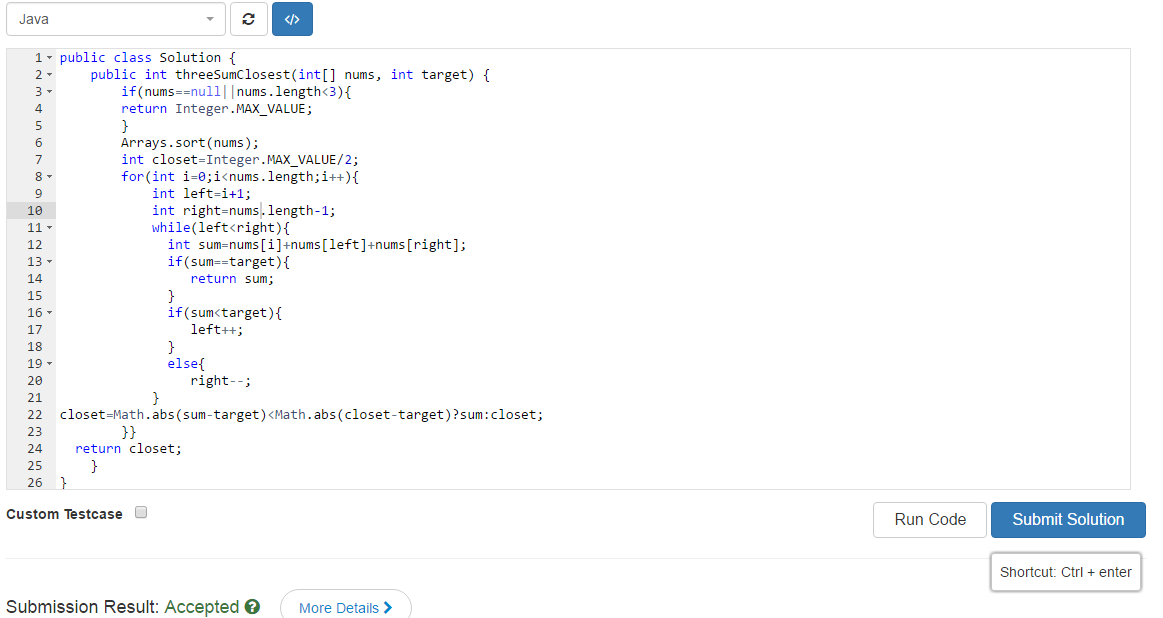
首先我们要有个大概的思路 第一步无疑是判断是否为空和满足三个数的条件

接下来我们对数据进行排序

从数组最小的数字开始进行for循环 将它与它右边第一个数left和数组的最后一个数right相加 获得一个总值 这个总值如果比目标值小将left加一 反之将right减一 如果正好等于 目标值 那么将结果直接返回 循环要维护一个closet值 这个值代表已知的SUM里面最接近target的sum值 循环结束 返回closet;

之所以把初始值设置为integer.max_value/2 是为了 closet-target这个操作不溢出

这段代码耗时22ms 附上细节

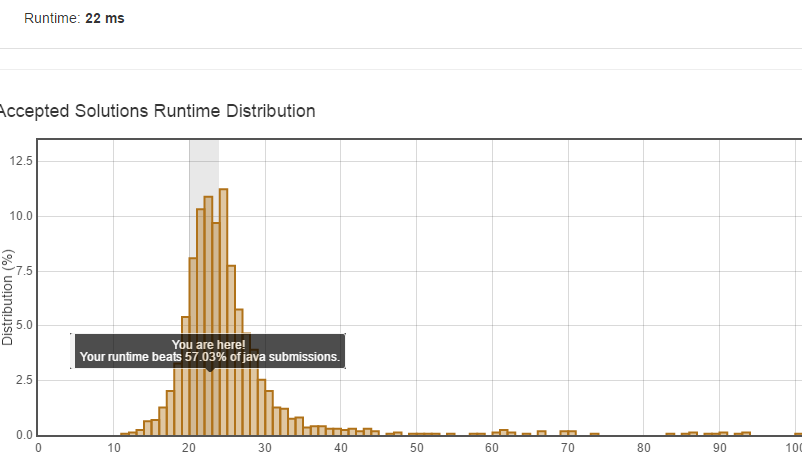
显然这段代码不是最优的 进去discuss看看别人的解法

有一段java 3/4ms的解法 果断进去看

public int threeSumClosest(int[] nums, int target) {
        Arrays.sort(nums);
        int n = nums.length, p = -1; // for getting closest sum3[p] to target
        int[] sum3 = new int[n-2];
        for (int i=0; i<n-2; i++) {
            sum3[i] = nums[i]+nums[i+1]+nums[i+2];
            if (sum3[i]==target) return target;
            if (sum3[i]<target) p = i;
        }
        if (p==-1) return sum3[0];
        if (p==n-3) return sum3[n-3];

        int l, m, r;
        if (target-sum3[p] <= sum3[p+1]-target) m = p+1; // (sum3[p]=nums[l]+nums[m]+nums[r])
        else m = p+2; // sum3[p+1] is the closest sum
        l = m-1;
        r = m+1;
        int gap = sum3[m-1]-target; // gap records the smallest gap to target for now

        while (l>=0 && r<=n-1) {
            int w = target-nums[l]-nums[r];
            int a = l+1, b = r-1;
            int tmp = Integer.MAX_VALUE; // tmp records smallest gap for m in (l,r)
            while (a<=b) {
                int t = nums[m] - w;
                if (t==0) return target;
                if (t>0) b = m-1;
                else a = m+1;
                if (Math.abs(t)<Math.abs(tmp)) tmp = t;
                m = (a+b)/2;
            }
            if (tmp>0) l--; // for nums[l]+nums[m]+nums[r], if smallest gap is positive, we need to make the sum less
            else r++;
            if (Math.abs(tmp)<Math.abs(gap)) gap = tmp;

之所以这段代码运行时间短 是因为它先做了预处理 不像我们的代码直接循环 并且先找到一个接近下标再进行循环 它先遍历一遍相邻的三个数之和 得到一个p值 如果P值没发生变化 那么整个说明没有找到和比target小的 无疑前三个的和就是答案 直接返回 相反如果P是最后三个数的和的第一个下标  那么说明 最后三个数的和都比target小 最后三个数的和无疑是最接近的 直接返回 便利过程中如果找到了和为target的直接返回结果