2019牛客暑期多校训练营（第六场）C Palindrome Mouse （回文树+DFS）

题目传送门

题意

给一个字符串s，然后将s中所有本质不同回文子串放到一个集合S里面，问S中的两个元素\(a,b\)满足\(a\)是\(b\)的子串的个数。

分析

首先要会回文树（回文自动机，一种有限状态自动机）

然后可以很轻松的求出来S集合，我们拿出一个样例画出回文树看一下

abacaba

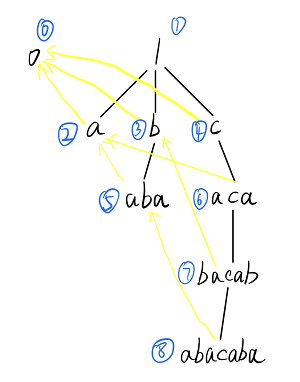
注: 上图中结点序号只是为了方便描述，与实际建树并不一定相同

0和1分别为偶数根和奇数根，黄边为fail边，总共有7个本质不同的回文串。

在计算答案时，我们从上到下统计，例如计算aba作为母串时的答案，那么子串有\(a\),\(b\)两个，

在计算\(bacab\)时，有\(aca, a, c, b,\) 四个。不难发现，如果把黄边也加入到整个树后，变成一张图，当我们计算某一结点（具体意义为一个回文串,比如7号节点）的答案时，我们要计算它的"祖先"（具有实际意义，即代表一个回文串，例如7号结点祖先为2，3，4，6）。

为了不重复记录，有必要标记我们已经考虑过的结点（也就是计算一个答案之后（比如7）再计算它的子节点的答案时（比如8），我们要把子节点的fail所指结点（比如5）和它自己（7）算进去），而在加这些新结点进行计算时要保证他们之前没有考虑过（比如5，但是7就不需要了，7肯定在之前没有考虑过）

但是不能只对5号结点标记访问，还需要对7标记已经访问，你可以看下面这个例子

在计算7号时，我们要把7号fail所指结点加到答案中去，但是按照我们之前的计算流程可以发现，i 已经在\(ehihe\)的祖先中了，所以不能重复添加。（因为这个坑wa了一发）

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 100010;
int T;
char s[N];
int n;
ll res;
namespace PAT{
    const int SZ = 2e5+10;
    int ch[SZ][26],fail[SZ],cnt[SZ],len[SZ],tot,last,dep[SZ];
    int vis[SZ];
    void init(int n){
        for(int i=0;i<=n+10;i++){
            fail[i] = cnt[i] = len[i] = vis[i] = dep[i] = 0;
            for(int j=0;j<26;j++)ch[i][j] = 0;
        }
        s[0] = -1;fail[0] = 1;last = 0;
        len[0] = 0;len[1] = -1,tot = 1;
        dep[0] = dep[1] = 0;
    }
    inline int newnode(int x){
        len[++tot] = x;return tot;
    }
    inline int getfail(int x,int n){
        while(s[n-len[x]-1] != s[n])x = fail[x];
        return x;
    }
    void create(char *s,int n){
        s[0] = -1;
        for(int i=1;i<=n;++i){
            int t = s[i]- 'a';
            int p = getfail(last,i);
            if(!ch[p][t]){
                int q = newnode(len[p]+2);
                fail[q] = ch[getfail(fail[p],i)][t];
                ch[p][t] = q;
            }
            ++cnt[last = ch[p][t]];
        }
    }
    int dfs(int p,ll tot){
        //printf("%d %d\n",p,tot);
        res += tot;
        int isadd = (p!=0&&p!=1);//如果爸爸是0号和1号，没实际意义，不计入答案
        vis[p] = 1;
        for(int i=0;i<26;i++){
            if(ch[p][i]){
                int nxt = ch[p][i];
                if(vis[fail[nxt]])
                    dfs(nxt,tot+isadd);
                else{
                    vis[fail[nxt]] = 1;
                    int isaddfail = (fail[nxt]!=0 && fail[nxt] != 1);
                    dfs(nxt,tot+isadd+isaddfail);
                    vis[fail[nxt]] = 0;
                }
            }
        }
        vis[p] = 0;
    }
    void calc(){
        dfs(0,0);
        dfs(1,0);
    }
}
int main(){
    scanf("%d",&T);
    int cas = 0;
    while(T--){
        scanf("%s",s+1);
        n = strlen(s+1);
        PAT::init(n);
        PAT::create(s,n);
        res = 0;
        PAT::calc();
        printf("Case #%d: %lld\n",++cas,res);
    }
    return 0;
}