Python练习题 043：Project Euler 015：方格路径

本题来自 Project Euler 第15题：https://projecteuler.net/problem=15

'''
Project Euler: Problem 15: Lattice paths
Starting in the top left corner of a 2×2 grid,
and only being able to move to the right and down,
there are exactly 6 routes to the bottom right corner.
How many such routes are there through a 20×20 grid?

Answer: 137846528820
'''

import itertools, time

startTime = time.clock()

# print(len(list(itertools.combinations([i for i in range(40)], 20))))

def factorial(x):
    t = 1
    for i in range(1, x+1):
        t *= i
    return t

print(factorial(40)//`(factorial(20)*factorial(40-20)))

print('Time used: %.2d' % (time.clock()-startTime))

原谅我智商低，这题我思考了一两天了也没想出来。参考网上 这篇文章 的分析，说是：

20*20的方格中，从左上角到右下角，不论怎么走，都只需要40步，其中必然有20步时横着走，20步时竖着走，你可以先全部先横着走，然后竖着走。所以这个问题变成了从40步中取出20步一共有多少种方法？用排列组合C（20上）（40下）。

个中算法俺真心不懂，不过求 C20/40 的组合值，不是有 itertools.combinations() 吗？我一试（也就是上面代码中被注释掉的那一行），结果电脑立马就死掉了——这得是多大的计算量啊~~~~~

后来查了下组合的计算公式：

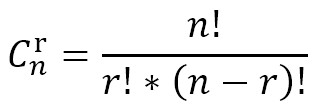
代入数值的话，就是：

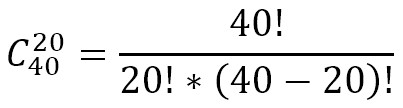
n! 表示计算阶乘（1 * 2 * 3 * ... * n），于是先定义个阶乘的函数，之后一引用计算就OK了，而且还死快！唉，看来以后还是得少用 itertools 里的方法了……

P.S.: 上述代入数值后的公式，因为分子分母都是乘来乘去的，40! = 20! * 21 * 22 * ... * 40，所以其实还可以把分子分母中的 20! 都约掉，这样还能减少点计算量。不过，对于计算机而言，这点优化几乎可以忽略不计，所以……就不折腾了~

那么，问题来了：为啥“这个问题变成了从40步中取出20步一共有多少种方法”呢？