Leetcode-dfs & bfs

102. 二叉树的层次遍历 https://leetcode-cn.com/problems/binary-tree-level-order-traversal/

给定一个二叉树，返回其按层次遍历的节点值。 （即逐层地，从左到右访问所有节点）。

解：

利用队列实现bfs，从根节点开始入队，如果左右子树不空，就入队。把每层的所有节点都遍历完了，下一层的最左节点再出队。（用for循环控制即可，因为在开始遍历新的一层之前，queue中只存了这一层的全部节点，batch process）。O(N)

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

import collections
class Solution:
    def levelOrder(self, root: TreeNode) -> List[List[int]]:
        if not root:
            return []

        queue = collections.deque()
        queue.append(root)

        # visited = set(root)  # 图的 bfs 需要 visited 标志

        res = []
        while queue:
            current_level = []
            level_size = len(queue)

            for _ in range(level_size):
                node = queue.popleft()
                current_level.append(node.val)
                if node.left:
                    queue.append(node.left)
                if node.right:
                    queue.append(node.right)

            res.append(current_level)
        return res

　　

dfs解决，开拓一下思路，递归的不断把level放下去，就把dfs遍历到的每个节点按level灌到res里面即可。

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def levelOrder(self, root: TreeNode) -> List[List[int]]:
        if not root:
            return []
        res = []

        def dfs(node, level):
            if not node:
                return
            if len(res) - 1 < level:  # res最后一行的索引比当前行的索引还小，说明当前行还没有进行任何遍历，放一个空list在res最后
                res.append([])

            res[level].append(node.val)  # 把node放到对应行去
            dfs(node.left, level+1)  # 遍历node的左右孩子
            dfs(node.right, level+1)

        dfs(root, 0)
        return res

　　

104. 二叉树的最大深度 https://leetcode-cn.com/problems/maximum-depth-of-binary-tree/

给定一个二叉树，找出其最大深度。

二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。

说明: 叶子节点是指没有子节点的节点。

解：

最直接的思路就是分治，递归实现，每个节点的深度为max(left, right) +1。

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def maxDepth(self, root: TreeNode) -> int:
        if not root:
            return 0
        return max(self.maxDepth(root.left), self.maxDepth(root.right)) + 1

　　

bfs，第一个出现的叶子结点所在的层是深度最小的，最后一个节点所在的层深度最大。

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def maxDepth(self, root: TreeNode) -> int:
        if not root:
            return 0
        queue = [root]
        max_depth = 0
        while queue:
            level_size = len(queue)
            if level_size:
                max_depth += 1
            for _ in range(level_size):
                node = queue.pop(0)
                if node.left:
                    queue.append(node.left)
                if node.right:
                    queue.append(node.right)
        return max_depth

　　

　　

dfs，从根节点开始按深度遍历，递归中按level向下，如果当前节点的level大于最大深度，最大深度就+1。

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def maxDepth(self, root: TreeNode) -> int:
        if not root:
            return 0

        max_depth = 1 # 根节点不空，至少为1
        def dfs(node, level):
            nonlocal max_depth
            if not node:
                return
            if max_depth < level:
                max_depth += 1
            dfs(node.left, level+1)
            dfs(node.right, level+1)
        dfs(root, 1)
        return max_depth

　　

111. 二叉树的最小深度 https://leetcode-cn.com/problems/minimum-depth-of-binary-tree/

最小深度是从根节点到最近叶子节点的最短路径上的节点数量。

说明: 叶子节点是指没有子节点的节点。

解：

分治，如果root左子树为空，最小深度就是右子树的最小深度+1；如果右子树为空，最小深度为左子树最小深度+1；如果左右都不空，分别找到最小深度，整体的最小深度为更小的深度+1

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def minDepth(self, root: TreeNode) -> int:
        if not root:
            return 0
        if not root.left:
            return self.minDepth(root.right) + 1
        if not root.right:
            return self.minDepth(root.left) + 1

        # 分治
        left = self.minDepth(root.left)
        right = self.minDepth(root.right)

        return min(left, right) + 1  # 聚合子问题的结果

　　

bfs，一层一层向下扩展，第一个出现的叶子结点深度最小

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def minDepth(self, root: TreeNode) -> int:
        if not root:
            return 0
        queue = [root]
        level = 0
        while queue:
            level_size = len(queue)
            if level_size:
                level += 1
            for _ in range(level_size):
                node = queue.pop(0)
                if not node.left and not node.right:  # 第一个叶子结点的深度最小
                    return level
                if node.left:
                    queue.append(node.left)
                if node.right:
                    queue.append(node.right)
        return level

　　

dfs

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

import sys
class Solution:
    def minDepth(self, root: TreeNode) -> int:
        if not root:
            return 0

        min_depth = sys.maxsize
        def dfs(node, level):
            nonlocal min_depth
            if not node:
                return
            if node.left is None and node.right is None:  # node 是叶子节点
                if level < min_depth:
                    min_depth = level
                    return

            dfs(node.left, level+1)
            dfs(node.right, level+1)

        dfs(root, 1)
        return min_depth

　　

22. 括号生成 https://leetcode-cn.com/problems/generate-parentheses/

给出 n 代表生成括号的对数，请你写出一个函数，使其能够生成所有可能的并且有效的括号组合。

解：

dfs + 剪枝，局部不合法，不再递归；左右括号都只能有n个；先加左括号；已经产生的序列中，左括号个数一定大于右括号的情况下，才能加右括号

class Solution:
    def generateParenthesis(self, n: int) -> List[str]:
        if n <= 0:
            return []

        res = []
        def dfs(left, right, n, result):   # 已用左括号个数，已用右括号个数，n，当前产生的括号序列
            nonlocal res
            if left == n and right == n:
                res.append(result)
                return

            if left < n:
                dfs(left+1, right, n, result+'(')

            if left > right and right < n:
                dfs(left, right+1, n, result+')')

        dfs(0, 0, n, '')
        return res

　　

46. 全排列 https://leetcode-cn.com/problems/permutations/

给定一个没有重复数字的序列，返回其所有可能的全排列。

解：

回溯，选第一个数，然后选剩下可选的数。

class Solution:
    def permute(self, nums: List[int]) -> List[List[int]]:
        if not nums:
            return[[]]

        ans = []

        def backtrack(nums, track):
            nonlocal ans
            if not nums:
                ans.append(track)
            else:
                for i in range(len(nums)):
                    # track加入当前选的nums[i], 下一层nums[i]也不能选了
                    backtrack(nums[:i]+nums[i+1:], track+[nums[i]])
                    # track自然的回退了，因为没有真的append上去

        backtrack(nums, [])
        return ans

　　

回退用交换来实现。

class Solution:
    def permute(self, nums: List[int]) -> List[List[int]]:
        if not nums:
            return[[]]

        ans = []
        n = len(nums)

        def backtrack(first):
            nonlocal ans
            if first == n:
                ans.append(nums[:])
            else:
                for i in range(first, n):
                    nums[first], nums[i] = nums[i], nums[first]  # 选第i个数加入解，把选择的数放nums最前面，因为原本在i之前的数下一轮是可以被选择的
                    backtrack(first+1)
                    nums[first], nums[i] = nums[i], nums[first]  # 回退

        backtrack(0)
        return ans

　　

78. 子集 https://leetcode-cn.com/problems/subsets/

给定一组不含重复元素的整数数组 nums，返回该数组所有可能的子集（幂集）。

说明：解集不能包含重复的子集。

解：

还是典型的回溯，不过因为是记录子集，每次track都记录一下就行了。

class Solution:
    def subsets(self, nums: List[int]) -> List[List[int]]:
        ans = []
        def backtrack(nums, track):
            nonlocal ans
            ans.append(track)
            for i in range(len(nums)):
                backtrack(nums[i+1:], track+[nums[i]])
        backtrack(nums, [])
        return ans

　　

或者直接迭代求解，这里设计的比较巧妙。每来一个新的数，就加到ans的中每个解中去，然后把新的ans和没加之前的ans合并。

class Solution:
    def subsets(self, nums: List[int]) -> List[List[int]]:
        ans = [[]]
        for i in nums:
            ans += [[i] + pre_solution for pre_solution in ans]
        return ans

　　

17. 电话号码的字母组合 https://leetcode-cn.com/problems/letter-combinations-of-a-phone-number/

给定一个仅包含数字 2-9 的字符串，返回所有它能表示的字母组合。

给出数字到字母的映射如下（与电话按键相同）。注意 1 不对应任何字母。

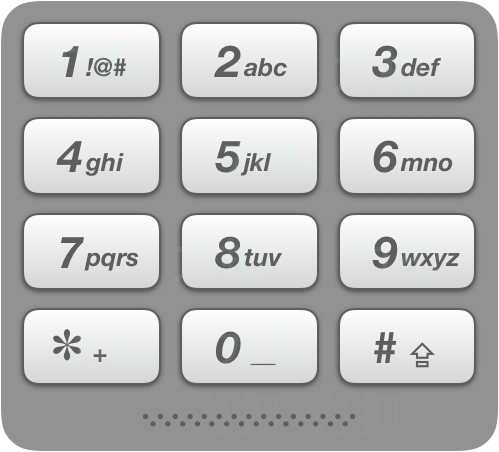
示例:

输入："23"
输出：["ad", "ae", "af", "bd", "be", "bf", "cd", "ce", "cf"].
说明:
尽管上面的答案是按字典序排列的，但是你可以任意选择答案输出的顺序。

解：

dfs，每个数字对应的可选择字符可以用哈希表先存好。按照dfs的框架

for c in choices:

　　# choose and add to track

　　dfs(nums, track)

　　# unchoose

class Solution:
    def letterCombinations(self, digits: str) -> List[str]:
        if not digits:
            return []
        words = {'2': 'abc', '3': 'def', '4': 'ghi', '5': 'jkl',
                 '6': 'mno', '7': 'pqrs', '8': 'tuv', '9': 'wxyz'}
        res = []
        n = len(digits)

        def dfs(i, track):
            nonlocal res
            if i == n:
                res.append(track)
                return
            else:
                for choice in words[digits[i]]:
                    dfs(i+1, track+choice)
        dfs(0, '')
        return res