B树【Balanced-Tree】

一、引言

　　B树是二叉平衡树的一个变种，在学习之前，我们先了解一下二分法，二叉树的一些相关的基本概念，有助于我们更好的理解B树~

二、二叉树

　　定义：二叉树即二叉平衡树

　　意义：通过二分法来进行元素查找，时间复杂度为O(logn)

　　查找元素的流程：

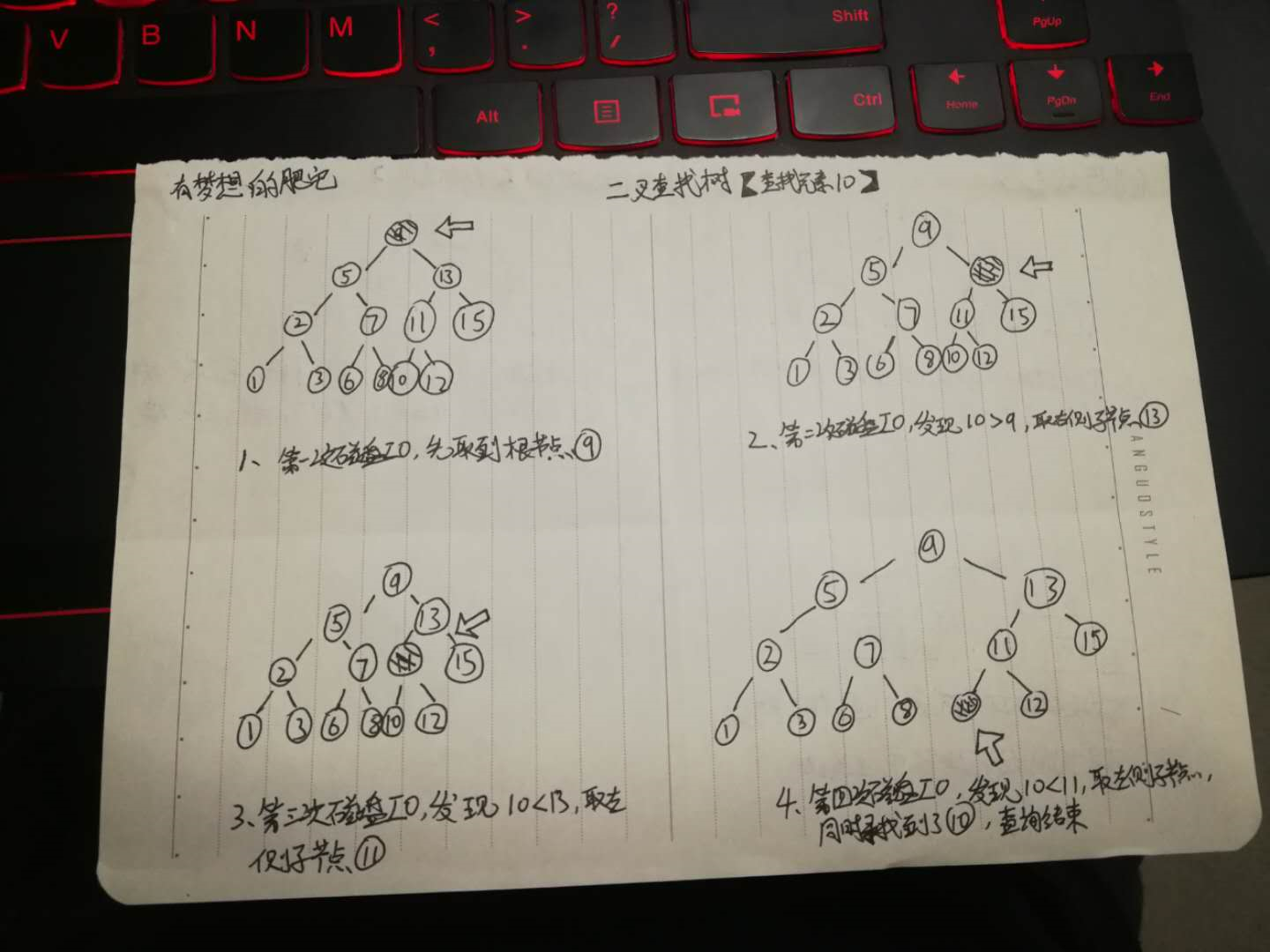
 　　解析：我们可以通过上图（画功有限，请见谅...）看到，二叉树具有以下几个特征：

• 非叶子节点都有2个分支【非叶子节点2个孩子】
• 左侧分支的值比右侧分支的元素要小【左小右大】
• 查询元素时通过与当前节点元素进行比较大小，若小于当前节点的元素走左侧分支，大于当前节点的元素时，则走右侧分支【查询时，小于走左边，大于走右边】

　　优势：

• 若非最悲观的情况（即查到最后一层）或者查询的层数不高的时候，可以比较快的返回相应的元素（但通常这个查询深度不可控，因为不确定查的元素在第几层）
• 每一个节点都存有对应的元素，若获取的元素正好在当前节点时，则不再继续往下走了，磁盘IO就会少一些。

　　劣势：

当查询深度较高时，会增加磁盘IO的次数，影响效率（图中以每取一次节点进行一次磁盘IO为例）

三、B树

　　定义：B树即多路平衡查找树

　　常见应用：文件系统和部分非关系型数据库的索引，如MongoDB

　　优势：树用作数据库索引主要是因为查询效率高，而且可以保持有序

　　查找元素的流程：

　　原则：一个m阶的B树（Balance Tree）具有如下几个特征：

• 1、根结点至少有两个子女。
• 2、每个中间节点都包含k-1个元素和k个孩子，其中 m/2 <= k <= m
• 3、每一个叶子节点都包含k-1个元素，其中 m/2 <= k <= m
• 4、所有的叶子结点都位于同一层。
• 5、每个节点中的元素从小到大排列，节点当中k-1个元素正好是k个孩子包含的元素的值域分划。

　　解析：我们可以对着上面的原则进行解析，图中是一个3阶的B树，那么m为3，m/2 <= k <= m则k可以取2，3，k-1就是1，2了。

• 1、根结点至少有两个子女【根节点是9，有2个子女】
• 2、每个中间节点都包含k-1【1~2】个元素和k【2~3】个孩子，其中 m/2 <= k <= m，满足
• 3、每一个叶子节点都包含k-1【1~2】个元素，其中 m/2 <= k <= m
• 4、所有的叶子结点都位于同一层。
• 5、每个节点中的元素从小到大排列，节点当中k-1【1~2】个元素正好是k【2~3】个孩子包含的元素的值域分划。

　　优势：

• 存放同样多的元素时，树的高度变小了，相当于减少了磁盘IO次数，提升性能
• 当查询进入了一个有很多元素的节点时，也只是存在于内存中进行比较，相对于磁盘IO的速度来说，消耗的时间可以忽略不计【这也是为什么在节点上进行“扩容”】

劣势：

• 相对于B+树来说，每个节点都会存数据，同样大小的磁盘页存的节点元素会少些
• 查询性能不稳定，比如有时可能会查到底层的叶子节点，有时可能查到最上层的根节点就返回了，每次查询的消耗不稳定，查询耗时波动大。
• 范围查询不方便，比如图中我要查询符合6~10的所有元素，而6~10的元素从根节点开始就分布在2侧的树中，所以需要经过的中序遍历非常繁杂

参考资料：

• 什么是B树