DFS搜索算法--（1）基础图遍历 绝对看！的！懂！

内容总结 自《啊哈！算法！》

作为一个都大二的了一个菜鸡，做题的时候DFS怎么可以不会呢！！！

作为一个都大二了的（！！！）菜鸡....《啊哈算法》这本书第四章的搜索，开始那里我就没看懂，就跑来看第五章了。结果这个理解起来方便一些....总结摘抄一下给远方的不知名网友and for myself。

以下语言有不严谨之处请多包涵，先理解重要。

深度搜索算法，就是对于一个图（图自己瞎画的  太丑）  如下图所示，给这些圆圈标号。

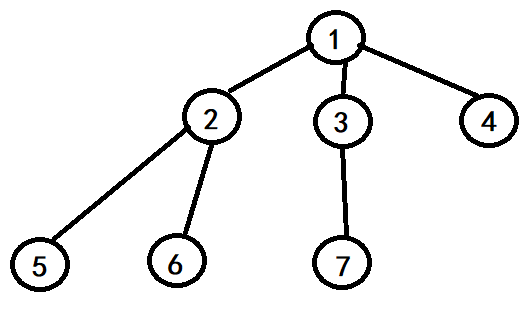
然后我们遍历的时候，是“优先深度” ，先从一条路走到黑走不动了再换条道继续一条路走到黑。即先从1开始，走到2，走到5. 然后走不动了就先回去，先回到2，发现还有6可以走，然后又走到6了。然后又走不动了。便回到2，但是2的所有支路已经都被访问过了，那就再往回走一个，走到1。 回到1以后，2这条道已经走完了，就走到3，再走到7，走不动了再回到3，3没有别的支路可以走了就再回到1，然后再走4

那么上图的访问顺序是（不算重复的顶点）：1  2  5  6  3  7  4

如果一条道走完了，比如说从2走到5，走完了，就要回到上一个路口顶点2。从5到2的过程称为回溯。

那么如何存储一个图呢？我们用一个二维数组arr来存储：

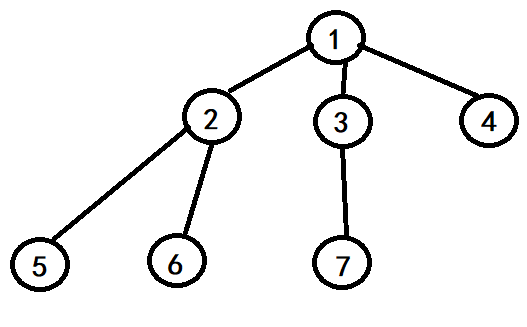
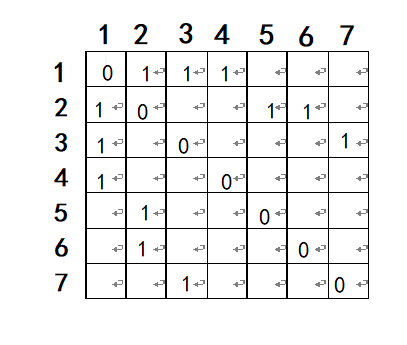
如上两个图所示，二维数组中第i行第j列表示的就是顶点i到顶点j是否有边。1表示有边，空着的就是没有边（在编程时可以将其赋值为9999，画图太麻烦我就省去了） ，二维数组行和列相等的我赋值为0.

能看到，上面的这个图是关于主对角线对称的，这是因为这个图是个‘无向图’。也就是这个图的边没有方向，从1到2和从2到1是一样的，所以 arr[ 2 ] [ 1 ] = arr[ 1 ][ 2 ] = 1。

以下是代码实现：

其中，book[  ]  这个数组一开始全部赋初值为0，表示未被访问过。被访问赋值为1。

还有一个需要知道的小知识点，就是我的代码内又两个return，第一个return表示函数结束，第二个return表示返回上一个dfs()函数，这是递归函数的特殊用法。比如：现在是dfs（5），执行代码时遇到了代码中第二个return，然后就会返回上一个执行的dfs()函数，这就变成了dfs(2)，这个过程就是回溯。

 void dfs(int cur)//cur是当前在的顶点的编号
 {
     printf("%d ",cur);//按顺序打印出遍历过的点
     sum++;//sum是全局变量，初值为0。每访问一个点，sum++。
     if(sum==n)
         return ;//n为全局变量，是总共点的数量。若sum==n，便是点都访问完了，就退出函数。

     for(int i=;i<=n;i++)//从1号点到n号点依次尝试，看看谁与cur点相连着
     {
         if(arr[cur][i]==&&book[i]==)//若这个点没有被访问过并且与cur相连
         {
             book[i]=;//把这个点标记为已访问
             dfs(i);//递归，继续从这个点再继续深入遍历
         }
     }
     return ;//当与cur相连的所有点都已被访问过了，就返回到上一个dfs（）
 }

完整代码如下：

 #include<iostream>
 #include<cstdio>
 using namespace std;

 int book[],sum,n,arr[][];

 void dfs(int cur)//cur是当前在的顶点的编号
 {
     printf("%d ",cur);//按顺序打印出遍历过的点
     sum++;//sum是全局变量，初值为0。每访问一个点，sum++。
     if(sum==n)
         return ;//n为全局变量，是总共点的数量。若sum==n，便是点都访问完了，就退出函数。

     for(int i=;i<=n;i++)//从1号点到n号点依次尝试，看看谁与cur点相连着
     {
         if(arr[cur][i]==&&book[i]==)//若这个点没有被访问过并且与cur相连
         {
             book[i]=;//把这个点标记为已访问
             dfs(i);//递归，继续从这个点再继续深入遍历
         }
     }
     return ;//当与cur相连的所有点都已被访问过了，就返回到上一个dfs（）
 }

 int main()
 {
     sum=;
     int m,a,b;
     cin>>n>>m;//m表示有几条边  n表示有几个点
     for(int i=;i<=n;i++){
         for(int j=;j<=n;j++){
             if(i==j)
                 arr[i][j]=;
             else
                 arr[i][j]=;//把没有边相连的标记为999999
         }
     }

     //读入顶点之间的那些边
     for(int i=;i<m;i++)
     {
         cin>>a>>b;
         arr[a][b]=;
         arr[b][a]=;//由于时无向图，所以两个都要标记。在前面我说过了
     }
     book[]=;//从1号顶点出发。标记1号顶点已经被访问
     dfs();

     getchar();getchar();

     return ;
 }

ok fine 那么简单图遍历就说完了  下次继续写